5.2. Математическая модель двигателя постоянного тока с независимым возбуждением (дпт нв).

С учетом предположений, сформулированных выше, считаем, что все параметры схемы замещения являются постоянными и . Тогда уравнение электрического равновесия по 2-му законом Кирхгофа:

, (5.1)

Уравнение движения электропривода:

. (5.2)

Или в канонической форме:

; (5.3)

. (5.4)

С учетом вышеупомянутых особенностей система уравнений МПТ будет линейной и допускает аналитическое решение. Но при исследовании параметры МПТ могут меняться и система уравнений становится нелинейной. Например, в случае, когда регулирование скорости обеспечивается сменой величины магнитного потока с учетом кривой намагничивания. При численном решении системы дифференциальных уравнений изменение параметров модели может быть легко учтено добавлениям необходимых дифференциальных или алгебраических уравнений. При использовании программ структурного моделирования необходимо построить структурную схему МПТ которая учитывает все особенности работы.

Разделим уравнение электрического равновесия на и введем обозначение электромагнитной постоянной времени:

. (5.5)

Тогда

, (5.6)

или в операторной форме:

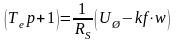. (5.7)

Принимая коэффициент передачи - , получим передаточную функцию по току в виде апериодического звена:

. (5.8)

Записав в операторной форме основное уравнение динамики получим передаточную функцию по скорости - передаточную функцию интегрирующего звена:

(5.9)

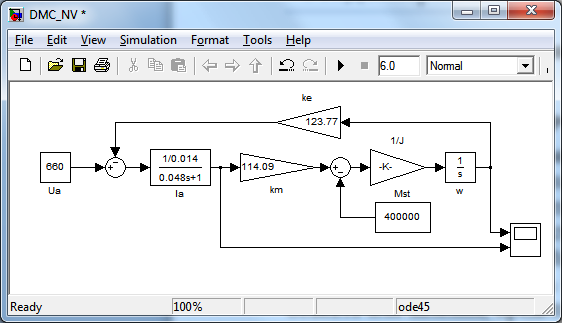
С учетом выражений и составим структурную схему двигателя постоянного тока, рис.5.3, а

а)

б)

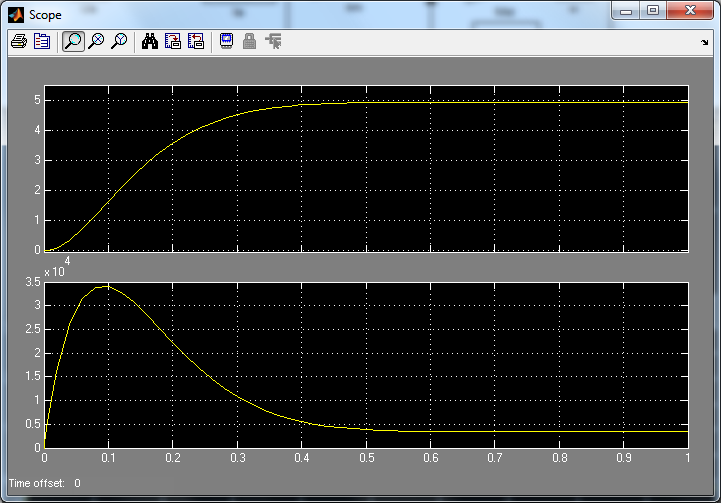
Рис.5.3. Структурная схема двигателя постоянного тока независимого возбуждения

5.3. Математическая модель двигателя постоянного тока с изменяющимся магнитным полем.

Магнитное поле ДПТ в процесес работвы может изменяться как в процессе регулирования тока возбуждения, та к и в силу конструктивных особенностей – наличия последовательной обмотки возбуждения, при достаточно большой величине реакции якоря и т.д.

Рассмотрим ДПТ последовательного возбуждения (ДПТ ПВ). Конструктивная особенность двигателя заключается в том, что магнитный поток является функцией тока якоря , причем эта зависимость нелинейная (рис.5.2).

Система уравнений для ДПТ смешанного возбуждения (ДПС СВ) аналогичная системе дифференциальных уравнений для ДПТ ПВ, за исключением того, что

,

где 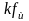- коэффициент потока от шунтовой (независимой) обмотки возбуждения.

Раньше указывалось, что такие особенности машины, как реакция якоря, влияние вихревых токов и др., в номинальных режимах не проявляются и ими можно презреть. Однако использование полученной структурной схемы позволяет легко учесть эти и другие характерные особенности физической картины процессов преобразования электрической энергии в механическую.

Рассмотрим работу МПТ с учетом реакции якоря.

Учитывая, что реакция якоря проявляется в изменении магнитного поля машины при изменении тока якоря, то полный магнитный поток:

где - поток, обусловленный действием тока возбуждения, - поток реакции якоря.

График имеет ориентировочно такой вид (рис.5.4.):

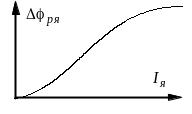
Рис.5.4. График зависимости

С учетом вышеизложенных соображений полный коэффициент потока ДПТ, Учитывающий действие обмотки последовательного возбуждения и действие реакции якоря,можно вычислить по формуле:

Обобщенная система дифференциальных уравнений для ДПТ:

(5.10)