Приложение 24

Объём выборки n определяется следующим образом:

1. Если величина ошибки и доверительная вероятность не имеют значения, то n ≈ N, где N – объём генеральной совокупности.

2. Если учитываются доверительная вероятность и абсолютное значение ошибки, то

,

Где σ²_выб – значение выборочного стандартного отклонения, полученного при пробном обследовании небольшой по объёму выборки (примерно 50);

Е – абсолютное значение допустимой ошибки;

K – поправочный коэффициент, величина которого определяется по графику

Пример.

Торговая фирма хочет открыть супермаркет на территории некоторого округа. Для проведения маркетинговых исследований руководству фирмы необходимо иметь информацию о годовых доходах семей, живущих в данном округе. Предварительные обследования показали, что доходы варьируются в пределах от 9000 до 29 000 руб. Однако для более надежных прогнозов необходима точность в размере Е = 200 руб. с доверительной вероятностью 95%. Требуется определить, сколько семей нужно обследовать, чтобы получить заданную точность оценки. Для определения стандартного отклонения σ_выб было проведено пробное обследование 50 семей. В результате была получена оценка стандартного отклонения σ_выб = 3000 руб.

По формуле n = k σ²_выб/Е² найдем необходимый объем выборки n = 864,36

Очевидно, выборка из 865 семей может обеспечить задан­ную ошибку.

Следует отметить, что точность оценки необходимого объе­ма п будет зависеть от достоверности информации о величине стандартного отклонения σ_выб .

Источник информации - Сулицкий В.Н. Методы статистического анализа в управлении: Учебн. пособие. – М.:Дело, 2002. – 520 с.

Приложение 25

Проверка адекватности модели

Проверка адекватности проводится на основе определения отклонения модельных значений от реальных. Показателями качества являются:

• коэффициент детерминации (определяется для нелинейных связей):

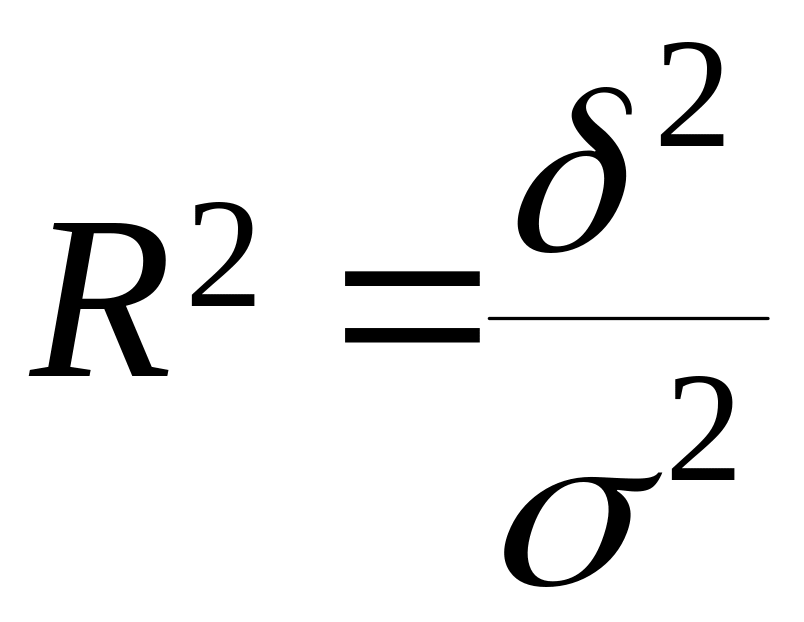
где σ² = δ² + ε²

Чем меньше рассеяние эмпирических точек вокруг модельной функции, тем меньше средняя ошибка аппроксимации. Ошибка аппроксимации менее 7% свидетельствует о хорошем качестве модели.

Приложение 26 Календарное планирование трудовых ресурсов

Ставится задача регулирования численности рабочих во времени при известной минимальной потребности путем найма и увольнения c учетом того, что имеют место убытки в виде некоторых накладных расходов (оплата услуг биржи труда, расходы на обучение, оформление документов и т. п.) и необходимость оплаты простоев при лишней численности.

Введем обозначения: - k - число недель до конца исследуемого периода, - B_k - минимальная потребность в рабочих на первой из них, - Y - наличие рабочих на этой неделе, - C1(Z_k) - убытки при превышении численности (Z_k>0), - C2(S_k) - расходы по найму (S_k>0).

Ecли обозначить через F_k(Y0) минимальные расходы в течение k недель при начальной численности Y₀, то при k > 1

Значения Y, обеспечивающие здесь минимум, дают оптимальную численность на первой из k недель (на первом шаге k - шагового процесса) при начальной численности Y0. Будем обозначать их через Y_k(Y0).

Пример. Пусть потребности в рабочих в течение 5 недель равны соответственно 5, 7, 8, 4 и 6. Функции затрат равны

Откажемся от единой сетки значений Y0. Так как перед последней неделей численность составляла не менее 4 человек, то отыскиваем

при возможной предыдущей численности Y0 = 4, 5, 6, 7 и т.д.

Т . к. искомая численность соответствует последнему шагу процесса, то использовать численность свыше 6 бессмысленно и минимум достигается при Y=6; при предыдущей численности 4 принять 2 рабочих, при численности 5 принять одного, при численности 6 приемане производить и при большей численности провести соответствующие увольнения (затраты на увольнение мы при постановке задачи не предусмотрели).

Так как перед четвертой неделей численность составляла не менее 8 человек, то

при возможной предыдущей численности Y0 = 8, 9, 10 и т. д.

Так как перед третьей неделей численность составляла не менее 7 человек, то

при возможной предыдущей численности Y0 = 7, 8, 9 и т. д.

Так как перед второй неделей численность составляла не менее 5 человек, то

при возможной предыдущей численности Y0 = 5, 6, 7 и т.д.

Наконец,

при возможной предыдущей численности Y0 = 0, 1, 2 и т.д.

Если начальная численность не превышала 6, то на первой неделе численность должна быть доведена до 5. На второй неделе численность доводится до 8, на третьей оставляется той же, на четвертой доводится до 6 и на последней остается неизменной.

При начальной численности 0 затраты составят

Если начальная численность составляла 7 человек, то численность на первой и второй неделях - 7, на третьей - 8 и на последних двух - 6. При начальной численности, большей 7 , на первые две недели устанавливается численность 7 или 8, на третьей - 8 и на последних - 6 .

Приложение 27

Таблица 1