9. Применение экономико-математических методов в дипломном проектировании

Математика подобна мясорубке, она может переработать любое мясо, но для того, чтобы получить хорошие котлеты, нужно и хорошее мясо.

Гексли

Широкое использование математических методов повышает эффективность принятия управленческих решений. Это достигается за счет сокращения сроков проведения анализа и планирования, более полного охвата влияния факторов на результаты коммерческой деятельности, замены приближенных или упрощенных расчетов точными вычислениями, постановки и решения новых многомерных управленческих задач, практически не выполнимых вручную или традиционными методами.

Применение того или иного математического метода в экономическом исследовании опирается на научно обоснованную классификацию методов и задач анализа и методологию экономико-математического моделирования хозяйственных процессов. Используя только два признака классификации, все экономико-математические методы делятся на четыре группы:

1. оптимизационные точные методы;

2. оптимизационные приближенные методы;

3. неоптимизационные точные методы;

4. неоптимизационные приближенные методы.

К оптимизационным точным методам можно отнести методы теории оптимальных процессов, некоторые методы математического программирования и методы исследования операций. К оптимизационным приближенным методам относятся отдельные методы математического программирования, методы исследования операций, методы экономической кибернетики, методы математической теории планирования экстремальных экспериментов, эвристические методы. К неоптимизационным точным методам относятся методы элементарной математики и классические методы математического анализа, эконометрические методы. К неоптимизационным приближенным методам относятся метод статистических испытаний и другие методы математической статистики.

Математическое моделирование экономических явлений и процессов является важным инструментом экономического исследования. Оно дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Модель  условный образ объекта управления (исследования). В экономическом исследовании используются главным образом математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств.

Процесс моделирования можно условно подразделить на три этапа:

1. Анализ теоретических закономерностей, свойственных изучаемому явлению или процессу, и эмпирических данных о его структуре и особенностях; на основе такого анализа формируются модели.

2. Определение методов, с помощью которых можно решить задачу.

3. Анализ полученных результатов.

Основная особенность стохастического факторного анализа заключается в том, что при его проведении нельзя составлять модель путем качественного (теоретического) анализа, необходим количественный анализ эмпирических данных.

В экономических исследованиях нашли применение следующие математико-статистические методы стохастического моделирования хозяйственных явлений и процессов:

• оценка связи и корреляции между показателями;

• оценка статистической значимости связей;

• регрессионный анализ;

• выявление параметров периодических колебаний экономических показателей;

• группировка многомерных наблюдений;

• дисперсионный анализ;

• современный факторный (компонентный) анализ;

• трансформационный анализ.

Математический аппарат вышеперечисленных экономико-статистических методов нашел достаточное отражение в учебниках по теории статистики.

Метод многофакторного регрессионного анализа применяется для построения модели, отображающей связь какого-либо показателя с другими показателями. Сначала в результате качественного анализа выделяется k факторов (X₁, X₂,..., X_k), влияющих, по мнению аналитика, на изменение прогнозируемого показателя Y, и строится чаще всего линейная регрессионная зависимость типа

(),

где A_i - коэффициенты регрессии, i = 1,2,...,k.

Значения коэффициентов регрессии (A₀, A₁, A₂,..., A_k) определяются в результате сложных математических вычислений, которые обычно проводятся с помощью стандартных статистических компьютерных программ.

Определяющее значение при использовании данного метода имеет нахождение правильного набора взаимосвязанных признаков, направления причинно-следственной связи между ними и вида этой связи, которая не всегда линейна.

Необходимость включения математико-статистических методов в методику дипломного проекта зависит от значимости решаемых при помощи данных методов количественных (статистических) задач.

Можно выделить следующие наиболее типичные классы задач в экономическом исследовании:

1. Изучение наличия, направления и интенсивности связи экономических показателей.

2. Ранжировка и классификация факторов экономических явлений.

3. Выявление аналитической формы связи между показателями.

4. Сглаживание (выявление тренда) динамики изменения уровня показателей.

5. Выявление параметров закономерных периодических колебаний уровня показателей.

6. Ранжировка и классификация предприятий и их подразделений.

7. Изучение размерности (сложности, многогранности) экономических явлений.

8. Выявление наиболее информативных (обобщающих) синтетических показателей.

9. Изучение внутренней структуры связей в системе экономических показателей.

10. Сравнение структуры связей в разных совокупностях.

При анализе временных рядов широко применяются графические методы. Это объясняется тем, что табличное представление временного ряда и описательные характеристики не позволяют понять характер процесса, а по графику временного ряда можно сделать определенные выводы, которые потом могут быть проверены с помощью расчетов:

наличие тренда и его характер;

наличие сезонных и циклических компонент;

степень плавности или прерывистости изменений последовательных значений ряда после устранения тренда.

Так графический анализ ряда обычно задает направление его дальнейшего анализа. В MS-Excel для этого можно использовать средство Мастер диаграмм.

В математически формализованной системе анализа, планирования и управления особое место занимают сетевые графики. Они дают большой экономический эффект при строительстве и монтаже промышленных и других предприятий. Применение сетевых графиков анализа, планирования и управления обеспечивает, как показывают многие примеры, сокращение сроков строительства на 20-30 %, повышение производительности труда на 15-20 %.

Приемы и алгоритмы нахождения критического пути и расчета соотношения «длительность/издержки» с помощью MS-Excel рассмотрены в [11]. В настоящее время на рынке программного обеспечения можно найти несколько программ, предназначенных для автоматизации процесса планирования, анализа и мониторинга проектов. Среди них MS-Project, Time Line, Primavera Project Planner, Spider Project.

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.

С помощью методов линейного программирования в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача о смесях в металлургическом производстве (состав доменной и агломерационной шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.

Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. В качестве примера приведем формирование оптимизационной модели, адекватной реальному процессу текущего планирования выпуска продукции и использования ресурсов:

где X = (x₁, x₂, … x_n) – вектор выпуска n видов продукции; с_j – цена (прибыль) реализации единицы продукции; a_ij – норма затрат i–го вида ресурса в производстве j–го вида продукции; b_i – имеющийся в наличии запас i–го вида ресурса; d_j и d_j – соответственно нижняя и верхняя границы выпуска продукции, чаще всего нижняя граница – обеспечиваемый заказами минимальный выпуск продукции, а верхняя – выпуск продукции, предусмотренный производственной мощностью или прогнозируемой величиной продаж.

Пример 2. В отделе технического контроля (ОТК) некоторой фирмы работают контролеры разрядов 1 и 2. Норма выработки ОТК за 8-часовой рабочий день составляет не менее 1800 изделий. Контролер разряда 1 проверяет 25 изделий в час, причем не ошибается в 98% случаев. Контролер разряда 2 проверяет 15 изделий в час; его точность составляет 95%.

Заработная плата контролера разряда 1 равна 80 руб. в час, контролер разряда 2 получает 60 руб. в час. При каждой ошибке контролера фирма несет убыток в размере 40 рублей. Фирма может использовать 8 контролеров разряда 1 и 10 контролеров разряда 2. Руководство фирмы хочет определить оптимальный состав ОТК, при котором общие затраты на контроль будут минимальными.

Математическая формулировка задачи.

Пусть X₁ и X₂ обозначают количество контролеров разрядов 1 и 2 соответственно. Число контролеров каждого разряда ограничено, т.е. имеются следующие ограничения:

X₁  8 (разряд 1)

X₂  10 (разряд 2)

Ежедневно необходимо проверять не менее 1800 изделий. Поэтому выполняется неравенство

825X₁ + 815X₂ = 200X₁ + 120X₂  1800,

или 5X₁ + 3X₂  45.

При построении целевой функции следует иметь в виду, что расходы фирмы, связанные с контролем, включают две составляющие:

1) зарплату контролеров.

2) убытки, вызванные ошибками контролеров.

Расходы на одного контролера разряда 1 в час составляют

80 руб. + 40250,02 руб. = 100 руб.

Расходы на одного контролера разряда 2 в час составляют

60 руб. + 40150,05 руб. = 90 руб.

Следовательно, минимизируемая целевая функция, выражающая ежедневные расходы на контроль, имеет вид

8(100X₁ + 90X₂) = 800X₁ + 720X₂.

Теперь можно сформулировать следующую задачу ЛП

F( ) = 800X₁ + 720X₂

при ограничениях

X₁  8

X₂  10

5X₁ + 3X₂  45

X₁, Х₂  0 .

Пример 3. Для выполнения n различных работ могут быть использованы рабочие m квалификационных групп. При выполнении j-й работы i-й группой рабочих выработка в единицу времени равна c_ij (i=1,...,m), ( j=1,...,n) рублей. Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышает b_i единиц времени, а объем j-й работы равен a_j рублей. Составить такой план выполнения работ, при котором производительность труда является максимальной.

Пусть X_ij - время, выделяемое рабочими i-й квалификационной группы на j-ю работу. Тогда

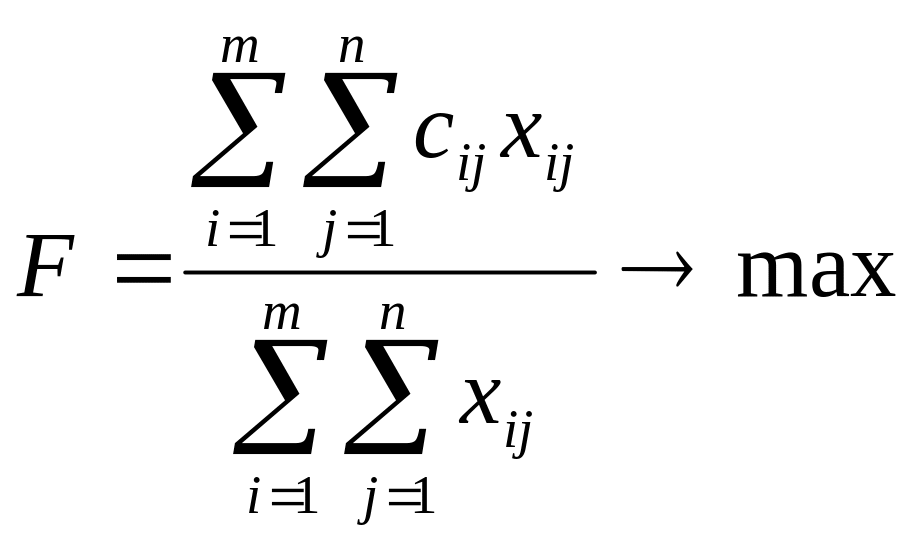    (производительность труда),

    (i=1,...,m) (ограничения на время),

    (j=1,...,n) (ограничения на объем работы),

    X_ij  0, (i = 1, ..., m), (j = 1, ..., n) – (условия неотрицательности).

Сформулированная выше задача может быть сведена к задаче линейного программирования.

Задачу линейного программирования можно решить с помощью надстройки Поиск решения в среде MS-Excel, используя технологии, описанные в [11, 17].

Теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных решений системы научных и хозяйственных экспериментов, с организацией статистического контроля, хозяйственных взаимоотношений между предприятиями промышленности и других отраслей. Формализуя конфликтные ситуации математически, их можно представить как игру двух, трех и т.д. игроков, каждый из которых преследует цель максимизации своей выгоды, своего выигрыша за счет другого.

Решение подобных задач требует определенности в формулировании их условий: установления количества игроков и правил игры, выявления возможных стратегий игроков, возможных выигрышей (отрицательный выигрыш понимается как проигрыш). Важным элементом в условии задач является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор данного игрока. Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. При исследовании конечной игры задаются матрицы выигрышей, а бесконечные – функции выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также сведение задачи к некоторой системе дифференциальных уравнений.

На промышленных предприятиях теория игр может использоваться для выбора оптимальных решений, например при создании рациональных запасов сырья, материалов, полуфабрикатов, в вопросах качества продукции и других экономических ситуациях. В первом случае противоборствуют две тенденции: увеличение запасов, в том числе и страховых, гарантирующих бесперебойную работу производства; сокращения запасов, обеспечивающих минимизацию затрат на их хранение; во втором – стремления к выпуску большего количества продукции, ведущего к снижению трудовых затрат; к повышению качества, сопровождающемуся часто уменьшением количества изделий и, следовательно, возрастанием трудовых затрат. В машиностроительном производстве противоборствующими направлениями являются стремление к максимальной экономии металла в конструкциях, с одной стороны, и обеспечение необходимой прочности конструкций – с другой стороны.

Методы оптимизма, пессимизма, Гурвица, Сэвиджа, «смещенного идеала», анализа иерархий могут использоваться при решении многокритериальных задач. Например, в отдел маркетинга требуется закупить принтер. Принтер должен быть недорогим, качественным (известной марки) и с доступными расходными материалами. Примеры решения задач такого рода рассмотрены в [2].

Теория массового обслуживания впервые применялась в телефонии, а затем и в других областях хозяйственной деятельности.

Например, организация нормального процесса обслуживания покупателей связана с правильным определением следующих показателей: количества предприятий данного торгового профиля, численности продавцов в них (в том числе и «механических»), наличия соответствующих основных фондов, частоты завоза товаров, численности обслуживаемого населения, плотности обращаемости и потребности в соответствующих товарах (по групповому и внутригрупповому ассортименту). Надлежит выбрать такой оптимальный вариант организации торгового обслуживания населения, при котором время обслуживания будет минимальным, качество  высоким, не будет излишних народнохозяйственных затрат. Математический аппарат теории массового обслуживания облегчает решение этой задачи. При этом различают две формы обслуживания: с неявными потерями и с явными потерями.

Существуют следующие виды систем массового обслуживания.

В зависимости от условий ожидания требованием начала обслуживания различают системы массового обслуживания с отказами и с ожиданием.

В системах с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются.

В системах с ожиданием требование, застав все обслуживающие каналы занятыми, становится на очередь вплоть до освобождения любого из каналов.

Системы, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ожиданием и ограниченной длиной очереди.

Системы, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.

Системы, допускающие очередь, но с ограниченным числом циркулирующих в системе требований, называются системами с ограниченным потоком требований.

По числу каналов обслуживания различают одноканальные и многоканальные системы.

По числу фаз обслуживания – однофазные и многофазные (последовательная обработка требований на нескольких каналах).

Систему массового обслуживания с неограниченной длиной очереди можно показать на следующем примере.

Механик из мастерской может обслужить 3 автомобиля в час. Клиенты появляются по 2 человека в час. Зарплата механика 70 руб./час, а затраты клиента 100 руб./час. Оценим параметры одноканальной системы массового обслуживания с ожиданием и неограниченной длиной очереди.

Определим коэффициент загрузки системы α:

α =  * ,

где  - среднее число требований, поступающих в единицу времени; μ - среднее число требований, удовлетворяемых в единицу времени.

α = 2 * = 0,67,

то есть механик занят 67% времени.

1. Вероятность отсутствия требований в системе

Р₀ = 1- α = 1- 0,67 = 0,33.

2. Вероятность того, что в системе находится более k = 3 требований

Р_n>k = α ^{k + 1} = 0,67^{3 + 1} = 0,132.

то есть в 13,2% случаев в мастерской более трех автомобилей.

3. Среднее число требований в системе

L_s = = 2 автомобиля.

4. Среднее время пребывания в системе

W_s = = 1 час.

5. Средняя длина очереди

L_q = L_s - α = 2 - 0,67 = 1,33 автомобиля.

6. Среднее время пребывания в очереди

W_q = = 0,67 часа или 40 мин.

Результаты расчетов приведены в табл. 1.

Таблица 1

Параметры	Одноканальная	Многоканальная
Р0	0,33	0,5
Ls	2 автомобиля	0,75 автомобиля
Ws	60 мин.	22,5 мин.
Lq	1,33 автомобиля	0,083 автомобиля
Wq	40 мин.	2,5 мин.
Затраты клиента	100 руб./час • 0,67 час. • 8 час./день • 2 авто/час = 1072 руб./день.	100 • 0,0415 • 8 • 2 = 70 руб.
Затраты мастерской	8 час/день • 70 руб./час = 560 руб./день.	8 • 70 • 2 = 1120 руб.
Суммарные затраты	1072 + 560 = 1632 руб.	1120 + 70 = 1190 руб.

При наличии двух мастеров время пребывания в очереди существенно сокращается и суммарные затраты меньше. Отсюда, целесообразнее иметь двухканальную систему, чем одноканальную.

Элементы теории нечетких множеств успешно применяются для принятия решений в условиях неопределенности. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами.

Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки

Рассмотрим пример применения метода аддитивной свертки для решения задачи по выбору некоторой фирмой, производящей бытовую технику, стратегии расширения своей доли на рынке.

Первоначально определяются альтернативы — возможные стра­тегии поведения фирмы.

Стратегия а₁ — снижение цены. Это возможно в том случае, когда фирма имеет некоторое преимущество перед конкурентами или может обеспечить снижение себестоимости продукции. Однако реализация этой стратегии может привести к ценовой конкуренции, что само по себе достаточно опасно.

Стратегия a₂ — модификация существующего продукта. Она потребует дополнительных расходов на переналадку производства, но при этом обеспечит некоторое повышение качества продукции. Реализация такой стратегии может привлечь новых покупателей, способствуя новому перераспределению долей рынка между фирмами. Конкуренция в данном случае не является ценовой и столь сильной.

Стратегия а₃ — разработка нового продукта. Эта стратегия потребует дополнительных и значительных расходов, но позволит в случае успеха опередить конкурентов в технологическом разви­тии и некоторое время быть монополистом на рынке.

Стратегия а₄ — поиск новых рынков сбыта. В этом случае фирма за счет поиска новых рынков и вхождения на них может увеличить объем продаж, но это не повлечет за собой перераспределение старого рынка. При такой стратегии также достаточно велика вероятность возникновения сильной конкурентной борьбы и возрастания расходов на маркетинговые исследования и новые производственные мощности.

Для оценки альтернатив определим следующие критерии: с₁ — затраты на расширение производства; с₂ — время реализации проекта; с₃ — затраты на маркетинговые исследования; с₄ — управленческие расходы; с₅ — риск от потерь; с₆ — срок окупа­емости; с₇ — качество продукции; с₈ — цена продукции.

Для оценки относительной важности критериев используется линг­вистическая переменная W = {ПРАКТИЧЕСКИ НЕВАЖНЫЙ; НЕ ОЧЕНЬ ВАЖНЫЙ; ДОВОЛЬНО ВАЖНЫЙ; ВАЖНЫЙ; ОЧЕНЬ ВАЖНЫЙ}. Значения термов множества заданы нечеткими числами, которые имеют треугольный вид функций принадлежности (рис. 1).

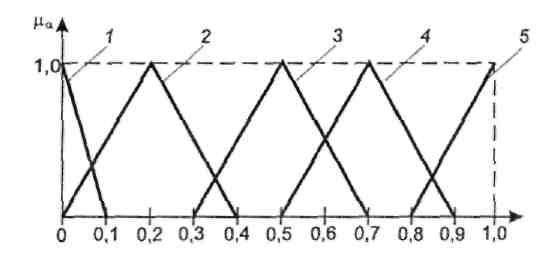
Рис. 1. Функции принадлежности термов важности критериев:

1 — практически неважный; 2 — не очень важный; 3 — довольно важный;

4 — важный; 5 — очень важный

Критерии получили следующие лингвистические оценки относительной важности а = {а_с1 = ВАЖНЫЙ; а_с2 = ДОВОЛЬ­НО ВАЖНЫЙ; а_Сз = НЕ ОЧЕНЬ ВАЖНЫЙ; а_с4 = ВАЖНЫЙ; а_С5 = НЕ ОЧЕНЬ ВАЖНЫЙ; а_С6 = ДОВОЛЬНО ВАЖНЫЙ; а_с7 = ВАЖНЫЙ; а_С8 = НЕ ОЧЕНЬ ВАЖНЫЙ}.

Оценка альтернатив по критериям производится с использованием лингвистической переменной S = "УДОВЛЕТВОРИТЕЛЬНОСТЬ" {КРАЙНЕ НИЗКАЯ; НИЗКАЯ; СРЕДНЯЯ; ВЫСОКАЯ; ОЧЕНЬ ВЫСОКАЯ}. Функции принадлежности термов имеют следующий вид:

КРАЙНЕ НИЗКАЯ = {1,0/0,0; 0,0/0,0};

НИЗКАЯ = {0,0/0,0; 1,0/0,2; 0,0/0,4};

СРЕДНЯЯ = {0,0/0,3; 1,0/0,5; 0,0/0,7};

ВЫСОКАЯ = {0,0/0,6; 1,0/0,8; 0,0/1,0};

ОЧЕНЬ ВЫСОКАЯ = {0,0/0,8; 1,0/1,0};

В табл. 2 сведены оценки рассматриваемых альтернатив.

Таблица 2