
Перелік контрольних питань
Подвійний інтеграл: визначення, геометричне тлумачення.
Властивості подвійного інтеграла.
Обчислення подвійного інтеграла в декартових координатах
Заміна змінної у подвійному інтегралі. Полярна система координат.
Геометричні та фізичні застосування подвійного інтеграла.
Потрійні інтеграли: визначення, властивості.
Обчислення потрійного інтеграла в декартових координатах.
Заміна змінних у потрійному інтегралі.
Циліндрична система координат.
Сферична система координат.
Геометричні та фізичні застосування потрійного інтеграла.
Криволінійний інтеграл І роду: визначення, обчислення.
Криволінійний інтеграл ІІ роду: визначення, обчислення.
Застосування криволінійних інтегралів.
Формула Гріна.
Умови незалежності криволінійного інтеграла від шляху інтеграції.
Поверхневі інтеграли І роду: визначення, властивості.
Обчислення поверхневих інтегралів І роду.
Поверхневі інтеграли ІІ роду: визначення, властивості.
Обчислення поверхневих інтегралів ІІ роду.
Зв’язок між поверхневими інтегралами І і ІІ роду.
Формула Остроградського.
Формула Стокса.
Скалярні та векторні поля.
Потік векторного поля: визначення, обчислення.
Дивергенція: визначення, обчислення.
Формула Остроградського-Гауса.
Ротор векторного поля: визначення, обчислення.
Потенціальне поле. Потенціал, його обчислення.
Циркуляція векторного поля.
Оператор Гамільтона.
Завдання для самостійної роботи Завдання 1
Обчислити площу фігури, обмеженої лініями
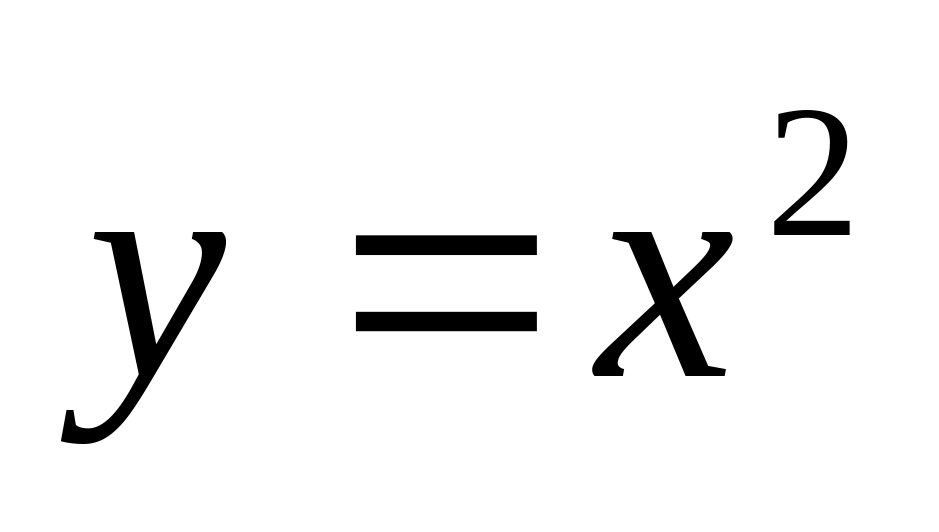 ,
y=
,
y= ,
y=0.
,
y=0.
 ,
x + y=2, y=0.
,
x + y=2, y=0.
x = 2, y=x, xy=1.
y
 =16-2x,
y=4-2x.
=16-2x,
y=4-2x.
y=x , y=8-x , xy
 1.
1.
y =4x, 2x-y=4, y
 0.
0.
4y=x , 6-2y=x .
x=4-y , x=4-2y , y=
 .
.
y =x+4, x+y=2, y 0.
x=4y-y , x=2y.
y=2-x, y =4x+4.
x=y -2y, 2y=x.
y = x, x+y=2.
 ,
x=
,
x= ,
x=0.
,
x=0.
xy=1, y=x, y=0, x=2.
y =16-2x, x-y=4.
y=x -6x+10, y=6x-x .
y=2x , y-x=3.
x=4y-y , y=x.
x=y -2y, x=2-y.
x= y , x=3y.
y= x -x, y=x+3.
x=y , y= x-6.
x=y +4, y=
 .
.
x =4y, 2y-x=4, x
 0.
0.
Завдання 2
Обчислити площу фігури, обмеженої лініями, використовуючи полярну систему координат
x +y =2x, x +y =4x, y=x, y=0.
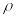 cos
cos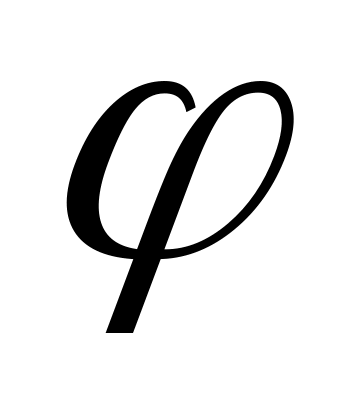 3,
3,
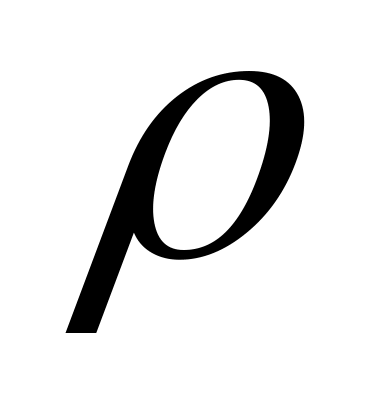 =6.
=6.
=2(1-cos ), =2.
x +y =6x, x +y =12x, y=x, y=0.
x +y =4y, y=x, x=0.
x +y =2x, x +y = 4x, y=
 x,
y=0.
x,
y=0.
=4+sin , =3.
x +y =6x, x +y =12 x, y= x, y=0.
x +y =20y, x=0, y=x.
x +y =x, x +y =2x, y=
 x,
y=0.
x,
y=0.
(x +y )
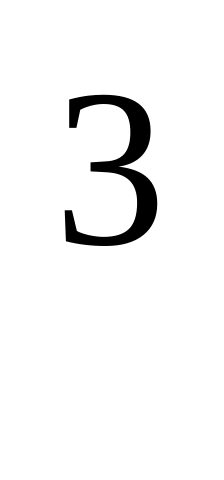 =
a
(x
=
a
(x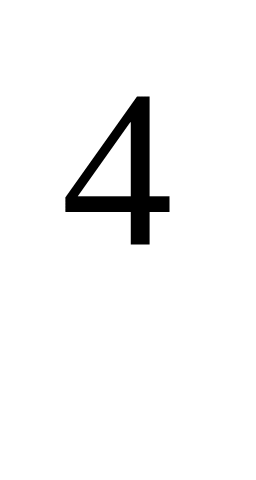 +
y
).
+
y
).
x + y = a xy.
=4(1+cos ), cos 3.
=3(1+cos ), =3cos .
(x +y ) =a (2x +3y ).
(x +y ) =a y .
(x +y ) =4ax .
(x +y ) =2a xy.
 8(1-cos
),
cos
6.
8(1-cos
),
cos
6.
x =a (x +3y ), 0
 x
x 2a.
2a.
(x +y ) =a (5x +3y ).
(x +y ) =a x (4x +3y ).
(x +y ) =a (4x +y ).
(x +y ) =a (3x +2y ).
(x +y ) =4ay .
