Нехай задане рівняння

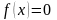, (1)

де 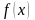– неперервна функція, визначена на проміжку 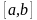і має різні знаки на кінцях цього проміжку, тобто виконується умова

(2)

Крім того, 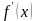та – неперервні і зберігають знак на проміжку . Необхідно знайти корінь рівняння (1) із заданою граничною абсолютною похибкою Е.

Поширеними методами розв’язку цієї задачі є метод поділу проміжку навпіл, метод хорд, метод Ньютона (дотичних), комбінований метод хорд та дотичних, метод простої ітерації, метод Ейткена–Стефенсона і метод Стефенсона.

1. Методи уточнення коренів нелінійних рівнянь Метод поділу проміжку навпіл

Цей метод є простим і надійним алгоритмом знаходження коренів рівняння (1).

Суть методу полягає в тому, що відрізок ділиться навпіл, тобто вибирається перше наближення кореня /рис.1/.

(3)

Якщо 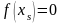, тоді 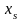є коренем рівняння (1).

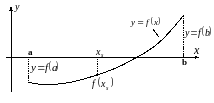
Рис.1.

Якщо , то вибирають той з відрізків чи 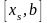, на кінцях якого функція має різні знаки. Одержаний відрізок знову ділять навпіл і т.д. Процес обчислень проводиться доти, доки величина відрізку 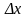не стане меншою від заданої похибки Е.

Метод досить стійкий до похибок заокруглень. Але й збігається теж повільно. При збільшенні точності значно зростає об’єм обчислень. Тому на практиці метод часто використовують для грубого визначення початкового наближення до кореня, а пізніше застосовують швидко збіжний ітераційний метод.

Алгоритм методу половинного ділення.

1. Задати значення параметрів а, b та граничної абсолютної похибки Е .

2. Обчислити значення функцій в точці а, тобто обчислити .

3. Поділити проміжок навпіл, тобто знайти точку

.

4. Перевірити умову ? Якщо так, то перейти до п.7.

5. Якщо добуток 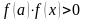, то 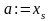, в протилежному випадку .

6. Якщо , то перейти до п.3.

7. Надрукувати (вивести) значення .

8. Закінчити виконання програми.

Значення е задається в межах 10 –410 –6.

Метод хорд

Цей метод забезпечує швидшу збіжність, ніж метод поділу проміжку навпіл. Ідея методу полягає в тому, що на достатньо малому проміжку функція змінюється лінійно і тому дуга кривої замінюється хордою, яка її стягує. За наближене значення кореня можна прийняти точку перетину хорди з віссю абсцис (точка А на рис.2)

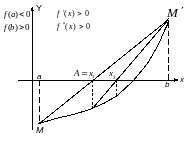Рис.2

Рівняння прямої, яка проходить через точки 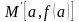і :

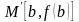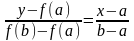
Точка А є наближеним коренем , яка була знайдена з рівняння прямої, якщо покласти 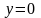, тоді :

(4)

Якщо значення кореня нас не задовольняють, його можна уточнити, застосувавши метод хорд до відрізку .

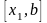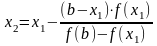(5)

Ітераційна формула методу хорд

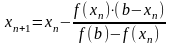
За наведеними формулами обчислюють корені і тоді, коли ; ; ; , тобто, коли .

У випадку, коли перша і друга похідні мають різні знаки, тобто ,то ітераційна формула має вигляд

(6)

Зауважимо, що формули (5) та (6) тотожні.

Обчислення виконуються доти, доки відмінність між двома послідовно обчисленими значеннями i 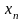не будуть меншими за Е

(7)

де Е – задана гранична абсолютна похибка.

Алгоритм методу хорд

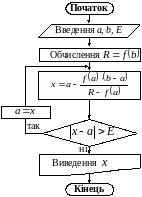
Метод Ньютона

Метод послідовних наближень, розроблений Ньютоном, широко використовується при побудові ітераційних алгоритмів. Цей метод відомий своєю швидкою збіжністю (квадратичною збіжністю).

Нехай корінь рівняння відокремлений на відрізку , причому і неперервні і зберігають сталі знаки на всьому відрізку . Геометричний зміст методу Ньютона полягає в тому, що дуга кривої 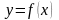замінюється дотичною до цієї кривої.

Візьмемо деяку точку x₀ відрізка [а, b] і проведемо в точці [x₀, f(x₀)] дотичну до цього графіку.

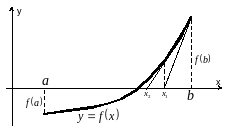
Рис. 3

Її рівняння має вигляд:

.

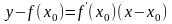Візьмемо за перше наближення кореня точку перетину дотичної з віссю ОХ, одержимо, що

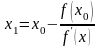(8)

Наступне наближення знаходимо відповідно за формулою

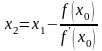
Ітераційна формула методу Ньютона має вигляд

(9)

Зазначимо, що початкове наближення доцільно вибирати так, щоб виконувалась умова

(10)

В протилежному випадку збіжність методу Ньютона не гарантується.

Найчастіше 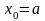або , в залежності від того, для якої із цих точок виконується умова (10).

Метод Ньютона ефективний для розв’язування тих рівнянь, для яких значення модуля і похідної 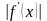біля кореня достатньо велике, тобто графік функції в околі даного кореня має велику крутизну.

Алгоритм методу Ньютона