Тема 3: Линейная многофакторная регрессионная модель

Постановка задачи

Исследовать зависимость одной зависимой переменной (Y) от нескольких объясняющих переменных ( Х , Х ,...,Х ) в условиях конкретного места и конкретного времени.

Эту задачу можно решить с помощью множественного или многофакторного регрессионного анализа.

Уравнение линейной множественной регрессии записывается в виде

Y= а + а X +а X +…+ а X .

Объясняющие переменные Х , Х ,...,Х оказывают совместное одновременное влияние на зависимую переменную У. Так как всех причин влияющих на результативный показатель (У) охватить нельзя, ( ограничившись, только важными объясняющими переменными), то в выражение функции регрессии вводят возмущающую переменную, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей, тогда эмпирические значения У можно представить

У=Y+U.

Рассмотрим функцию линейной множественной регрессии с двумя объясняющими переменными

Y= а + а X +а X .

Исходные данные запишем в матричном виде

У= , Х= .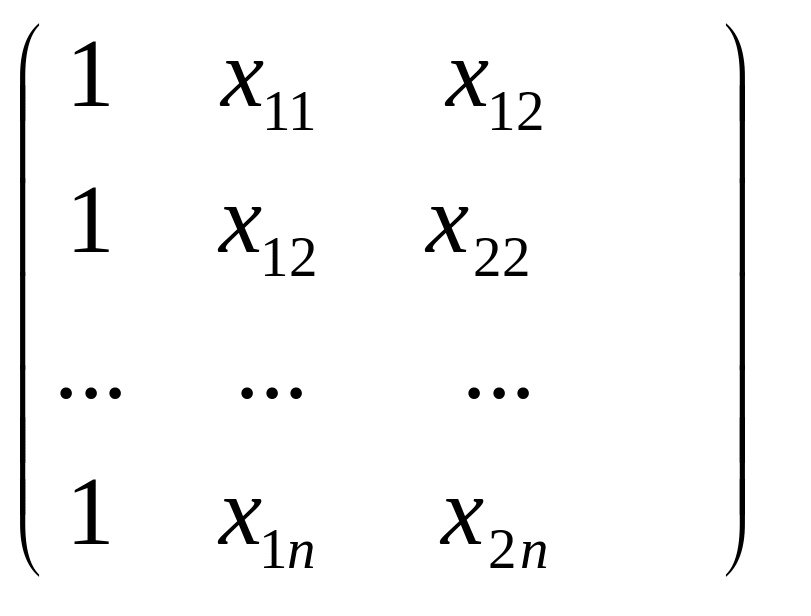

Задача состоит в оценке параметров а , а ,а регрессии по результатам выборочных наблюдений над переменными, включенными в анализ. Поставим условие, согласно которому регрессия должна по возможности хорошо согласовываться с эмпирическими данными. Поэтому выдвигаем требование, по которому сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии (т.е. сумма квадратов остатков) должна быть минимальной.

S (а , а ,а ) = = min.

Находим частные производные по а , а ,а и приравниваем к нулю. Т. о. будет получена стандартная форма системы нормальных уравнений:

= а n + a x + a x

x = а x + a x + a x x

x = а x + a x x +a x

Коэффициенты системы нормальных уравнений перед переменными а , а ,а представляют собой XX .Найдем произведение двух матриц Х и Х

Х =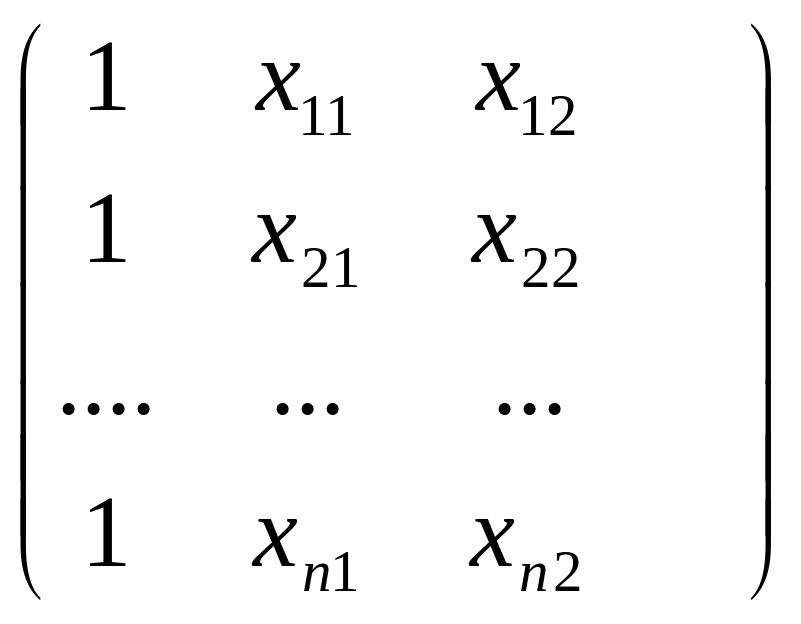 X =

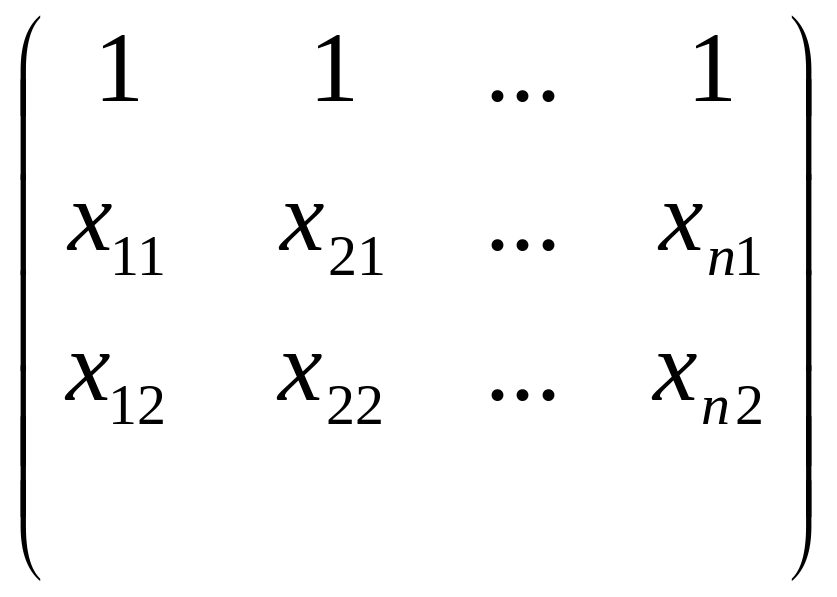
X X= .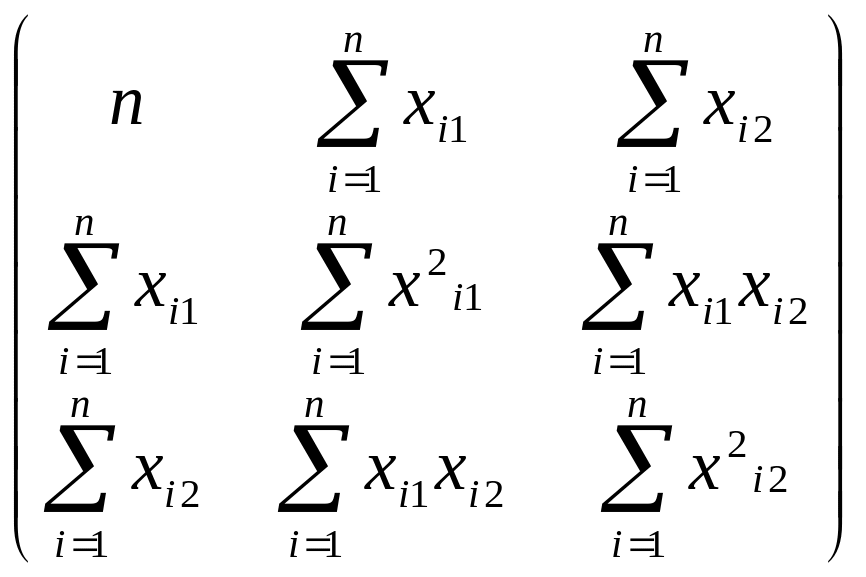

Найдем произведение X У= .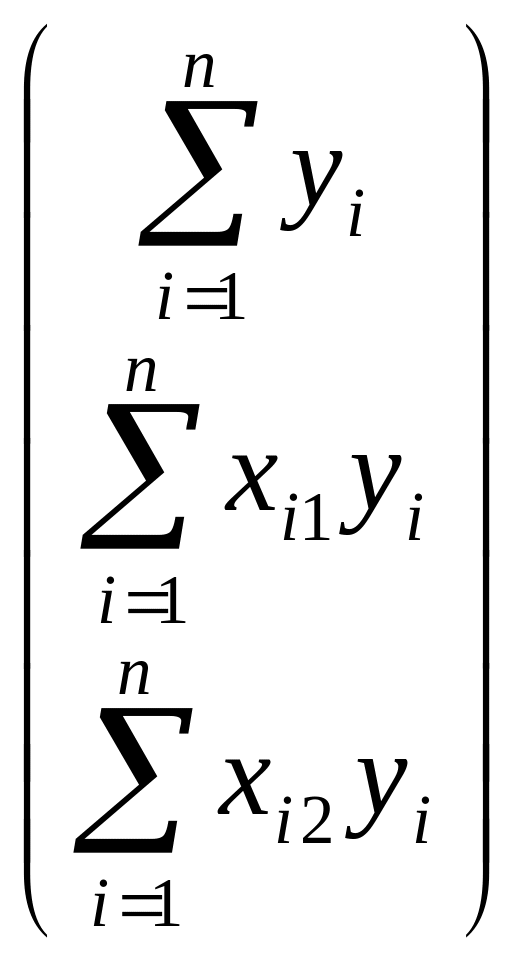

Т.о. систему нормальных уравнений можно записать

X X = X У

Если матрица X X обратима, то, умножив слева на ( X X) получим = ( X X) (X У).

Вычислив X X , ( X X) ,(X У), ( X X) ( X У), найдем значения а , а ,а .

Выражение X X можно записать для любого числа объясняющих переменных.

Оценка точности линейного множественного регрессионного анализа

Результаты различных выборок имеют различное рассеяние. Поэтому может случится, что построенная регрессионная зависимость одного итого же смысла по данным двух выборок из одной и той же генеральной совокупности приведет к различным уравнениям. Степень соответствия уравнений опытным данным может быть различна, поэтому для оценки степени соответствия регрессии имеющимся эмпирическим данным можно выбрать коэффициент детерминации. Коэффициент детерминации отражает, в какой мере функция регрессии определяется объясняющими переменными, содержащимися в ней.

Коэффициент множественной детерминации В - показывает какая часть общей дисперсии может быть объяснена зависимостью переменной Y от объясняющих переменных х ,х ,…,х .

В = .

Свойства коэффициента множественной детерминации

1. 1. 0 В 1

2. 2. Если В = 1, то y =у .

3. 3. Если В = 0, то y = отсутствует линейная зависимость.

Проверка значимости коэффициента множественной детерминации

При выполнении процедуры (проверки значимости коэффициента детерминации) выдвигается нулевая гипотеза H и альтернативная H .

H : существенного различия между выборочным коэффициентом детерминации и коэффициентом детерминации генеральной совокупности B=0 нет.

Эта гипотеза равносильна тому, что

a = a = a =…= a =0,

т.е. ни одна из объясняющих переменных, включенных в регрессию, не оказывает существенного влияния на зависимую переменную.

H : выборочный коэффициент детерминации существенно больше коэффициента детерминации генеральной совокупности B=0. Гипотеза H означает, что, по крайней мере, одна из m объясняющих переменных, включенных в регрессию, оказывает существенное влияние на переменную Y.

Оценка значимости коэффициента множественной детерминации производится с помощью F статистики

F= (1)

Которая имеет F- распределения Фишера с f =m и f =n-m-1 степенями свободы, где n – число наблюдений, m-количество объясняющих переменных включенных в модель. Вычисленное значение F статистики (1) по эмпирическим данным сравнивается с табличным F при заданном уровне значимости =0.05 или =0.01и соответствующем числе степеней свободы.

Если F F то вычисленный коэффициент детерминации значимо отличается от нуля. Этот вывод обеспечивается с вероятностью 1- .