Реализация аф нижних частот
Передаточная функция (5) может быть реализована в схеме, состоящей из звеньев с передаточными функциями первого и второго порядка. Количество звеньев будет определяться порядком проектируемого фильтра. Например, фильтр пятого порядка любого типа будет состоять из одного звена первого порядка и двух звеньев второго порядка. Передаточная функция такого фильтра имеет вид
.
(15)
Звено первого порядка может быть построено по схеме рис. 2. Найдем его передаточную функцию. При расчете будем пользоваться идеализированными характеристиками ОУ. Идеализация сводится к двум правилам: 1) напряжение между входами ОУ, охваченного отрицательной обратной связью, равно нулю (так называемый принцип виртуального замыкания входов); 2) на входы ОУ ток не поступает (виртуальный обрыв входных цепей). Используя оба правила, составим уравнение
,
где
.
Из уравнения находим
,
.
(16)
Для построения звеньев второго порядка используем схему, изображенную на рис.5.
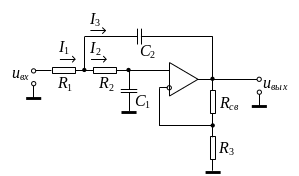
Рис. 5. Схема звена АФ второго порядка.
Выведем выражение для передаточной функции. Из схемы следуют уравнения
,
,
,
где
.
Из первых двух уравнений найдем
и подставим в третье. Из него получим
,
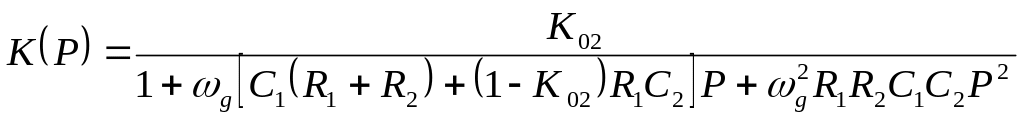где
.
Расчеты звена можно упростить, положив
и
.
Тогда
.
(17)
Отметим, что при
схема становится генератором сигналов
с частотой
.
В частности, значения коэффициента
усиления близкие к «3» возникают в
звеньях фильтров Чебышева высоких
порядков. В этом случае требуется
тщательная настройка, не допускающая
возникновения генераторного режима.
Передаточные функции (16) и (17) служат
основой для расчета номиналов резисторов
и емкостей в схемах фильтров. Реализуя
отдельные звенья с помощью схем рис. 2
и рис. 5, получаем передаточную функцию
в виде произведения выражений (16), (17).
Сопоставляя с передаточной функцией
(5), можно составить уравнения для
нахождения в i-том
звене значений
по значениям
.
Для звена первого порядка будет одно
уравнение
.
(18)
Для звеньев второго порядка после простых преобразований получим два уравнения
,
.
(19)
Из способа расчета следует, что фильтры различных типов могут быть реализованы с помощью одних и тех же схем, отличающихся лишь номиналами входящих в них элементов.
Пример расчета схемы фильтра
Выполним следующее задание:
построить схему фильтра нижних частот
Чебышева пятого порядка с неравномерностью
АЧХ в полосе пропускания не более
,
усилением
(40 дБ) и частотой среза
.
Расчет разделим на несколько этапов.
1. Согласно таблице 1, коэффициенты передаточной функции будут иметь следующие значения
,
,
,
,
.
2. Найдем коэффициенты усиления
отдельных звеньев. Используем второе
уравнение (19) и значение общего коэффициента
усиления фильтра:
.
Тогда
,
,
.
3. Выполним расчет элементов схемы
первого звена (обозначения по рис. 2).
Как следует из (18), номинал одного из
элементов
можно
задать, а другой рассчитать. Пусть
,
тогда
.
Ближайшее номинальное значение из
стандартного ряда Е24 будет
.
Для симметрии входных цепей ОУ по постоянному току (симметрия существенно уменьшает смещение нуля ОУ) необходимо выполнить условие
.
Отсюда находим
и
.
и
.
4. Выполним расчет элементов схемы
второго звена (схема рис. 5 с
и
).
Согласно первому уравнению (19) можно
выбрать С и рассчитать R.
Пусть
,
тогда
,
.
Условие симметрии входных цепей ОУ дает
(с учетом, что
)
.
Отсюда
и
.
и
.
5. Аналогично рассчитаем элементы
третьего звена. Выберем
.
Тогда
,
.
и
.
и
.
В результате расчета получена схема, изображенная на рис. 6 (с точными значениями рассчитанных сопротивлений). В задании по КНИРС необходимо построить и исследовать модели фильтров Чебышева и Бесселя как с точными, так и с округленными до номиналов ряда Е24 значениями сопротивлений.
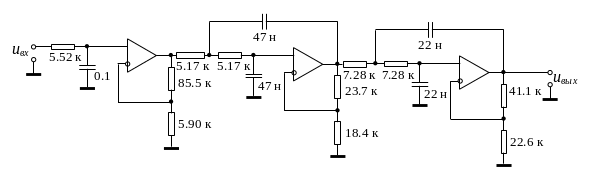
Рис. 6. Схема фильтра Чебышева 5-го порядка с неравномерностью АЧХ 1 дБ, усилением 40 дБ и частотой среза 1 кГц.