КНИРС 20

Государственное образовательное учреждение высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана» (МГТУ им. Н.Э. Баумана) Калужский филиал

В.В. Шагаев

Построение и исследование моделей активных фильтров Методические указания по выполнению книрс по специальности 210201

«Проектирование и технология радиоэлектронных средств»

(6-й семестр)

Калуга, 2013

Обсуждено и одобрено на заседании кафедры

«Конструирование и производство электронной аппаратуры»,

протокол № от « » 20 г.

Оглавление

Введение 4

Основные понятия теории фильтров 4

Активные фильтры нижних частот 6

Фильтры Баттерворта 6

Фильтры Чебышева 7

Фильтры Бесселя 10

Реализация АФ нижних частот 11

Пример расчета схемы фильтра 13

Принципы построения активных фильтров верхних частот и

полосовых фильтров 14

Моделирование фильтров с помощью программы Electronics Workbench 15

Литература 18

Контрольные вопросы 18

Задание по КНИРС 19

Введение

Основу пассивных частотных фильтров составляют LC- или RC-цепи. Схемы простейших фильтров нижних частот показаны на рис. 1.

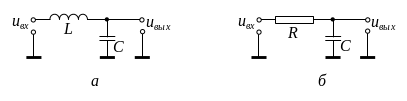
Рис. 1. Пассивные фильтры.

Пассивные фильтры обладают существенным недостатком – их свойства зависят от нагрузки. В активных фильтрах (АФ) в качестве элемента схемы используется операционный усилитель (ОУ). На рис. 2 изображена схема АФ, являющаяся совмещением обычной интегрирующей цепи и неинвертирующего усилителя. Введение в схему ОУ позволяет сравнительно просто решить проблему согласования фильтра с нагрузкой, и, кроме того, появляется возможность усиления сигнала.

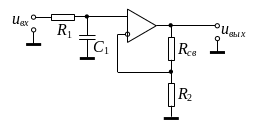
Рис. 2. Простейший активный фильтр.

Потребность в АФ возникает и в тех случаях, когда необходимо отфильтровать сигнал от помех, близких по частоте, не используя при этом катушек индуктивности. Стремление исключить катушки индуктивности связано в первую очередь с их большими габаритами, особенно на низких частотах. Вместе с тем схемы АФ могут быть спроектированы на основе достаточно жестких требований к их частотным и фазовым характеристикам.

Основные понятия теории фильтров

Для описания свойств фильтров используется коэффициент передачи. По определению, это отношение напряжения на выходе к напряжению на входе для гармонического комплексного сигнала с частотой f

. (1)

Здесь - входной сигнал; – круговая частота; функция называется амплитудно-частотной характеристикой (АЧХ), а – фазочастотной характеристикой (ФЧХ) фильтра. Например, для фильтра, изображенного на рис. 1б, имеем

, , . (2)

Если ввести безразмерную частоту и сделать замену переменной

,

то коэффициент передачи преобразуется в передаточную функцию

.

Как правило, в фильтрах нижних частот (ФНЧ) в качестве «обезразмеривающего» параметра выбирают верхнюю границу интервала , на котором уменьшается в раз (примерно на 3 дБ). В этом случае называют частотой среза фильтра. Очевидно, что выбор граничной частоты условен, поэтому везде ниже будет оговариваться критерий выбора этой частоты. Функция является аналитическим продолжением коэффициента передачи с мнимой оси на всю плоскость комплексных частот . На основе функции реализуется наиболее общий подход к исследованию радиотехнических цепей (метод преобразования Лапласа). Изучение этого подхода, однако, не входит в нашу задачу. Тем не менее, наряду с будем использовать функцию – это позволит упростить запись некоторых выражений и сделает изложение теоретического материала близким к общепринятому. В качестве примера приведем передаточную функцию RC-фильтра (рис. 1б, )

.

Из выражений (2) следует, что при будет . Такая зависимость приводит к снижению коэффициента передачи на 20 дБ на декаду. Если же необходимо получить более быстрое уменьшение коэффициента передачи, можно последовательно включить n фильтров. Тогда при больших значениях коэффициент передачи уменьшается на (20n) дБ на декаду. В общем случае передаточная функция цепочки из RC-фильтров имеет вид

. (3)

Далее будет показано, что АФ с требуемым уменьшением коэффициента передачи могут быть построены из звеньев с передаточными функциями двух видов

, , (4)

где – действительные положительные числа, – коэффициенты передачи постоянного сигнала ( ). Подчеркнем, что элементарными звеньями АФ могут быть как звенья с линейными, так и звенья с квадратичными полиномами в знаменателе. Причем, последние не имеют действительных корней. Данное обстоятельство означает, что звенья с передаточными функциями не могут быть реализованы с помощью пассивных цепей. В наиболее общем случае передаточная функция АФ описывается выражением

. (5)

При перемножении в знаменателе всех выражений в скобках образуется полином по переменной P. Степень полинома определяет порядок фильтра. Для нечетных порядков . Например, формулы (4) соответствуют фильтрам первого и второго порядка. Значения коэффициентов выбирают, исходя из критериев оптимизации характеристик проектируемого фильтра. Следующий раздел посвящен рассмотрению способов задания оптимальных характеристик ФНЧ.