4.12. Вплив температури на швидкість біохімічних реакцій

Швидкість хімічних реакцій значною мірою залежить від температури. У загальному вигляді швидкість реакції можна записати таким чином:

v = k(T)c^m, (4.84)

де k(T) – константа швидкості реакції, яка залежить від температури; c – концентрація; m – порядок реакції. Проаналізувавши експериментальні температурні залежності, Я. Вант-Гофф, а пізніше С. Арреніус (1889) запропонували емпіричну залежність швидкості реакції від температури:

(4.85)

де E_a – енергія активації; А – передекспоненційний множник, який відображає ймовірність перебігу реакції. Рівняння (4.85) називається рівнянням Арреніуса. Енергія активації Е_а – це енергетичний бар’єр, який переборюють молекули для здійснення реакції (рис. 4.34).

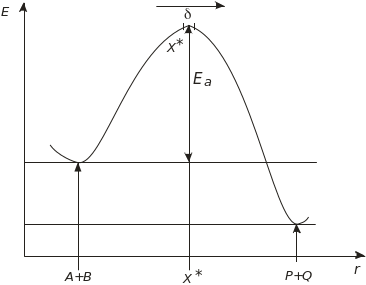
Рис. 4.34. Енергетична крива хімічної реакції:

Е – енергія; Е_а – енергія активації; r – координата реакції; Х^ – активований комплекс. Передекспоненційний множник А – це частота зіткнень реагуючих молекул

Тоді експоненційний множник (множник Больцмана) визначає частку ефективних зіткнень співударів, які приводять до хімічної реакції.

Рис. 4.35. Графік Арреніуса:

k – постійна швидкості реакції; Т – температура;  - кут нахилу прямої

Для визначення Е_а експериментальні дані подаємо у координатах Арреніуса (рис. 4.35):

. (4.86)

Отримуємо лінійну залежність . З нахилу прямої знаходимо Е_а:

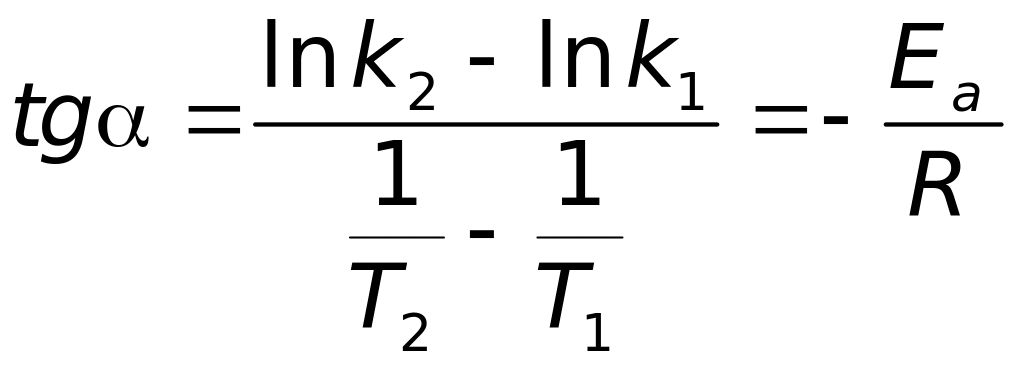. (4.87)

Перше пояснення температурної залежності швидкості реакції було зроблено на базі теорії співударів молекул у газовій фазі (В. Мак-Люіс, 1910). Пізніше було розроблено теорію абсолютних швидкостей реакцій (теорію перехідного стану) (Г. Ейрінг, 1935), яка пояснює хімічні реакції й ферментативні реакції в розчині. Ця теорія зв’язує швидкість реакції з термодинамічними характеристиками реагуючих молекул. Теорія абсолютних швидкостей реакцій на відміну від теорії співударів розглядає хімічну реакцію як складний багатоступеневий процес взаємодії ядер та їхніх електронних оболонок, а не просто співударів двох “кульок”. За теорією абсолютних швидкостей реакцій, перехід реагуючих молекул у продукти реакції відбувається через проміжний стан зі збільшеною енергією, який називається активованим комплексом. Утворення такого комплексу лімітує швидкість проходження будь-якої хімічної реакції. Утворення й розпад активованого комплексу зручно описувати через залежність потенційної енергії Е реагуючих молекул від координати реакції r (рис. 4.34). Координата реакції визначає таку траєкторію перебігу реакції, коли елементарні переходи реагуючих молекул від одного стану до іншого відбуваються з мінімальними енергетичними ефектами. На цій траєкторії існуватиме така критична координата r₀, коли всі реагуючі атоми зближені й утворюють активований комплекс Х. Активований комплекс з максимальною енергією перебуває в нейстійкому, перехідному стані.

За теорією перехідного стану, швидкість реакції визначається швидкістю проходження через вершину  потенціального бар’єра. Припускається, що в реакції

. (4.88)

Є певна концентрація активованих комплексів , які перебувають у “квазірівновазі” з початковими реагентами. Константу рівноваги можна записати цього процесу як:

. (4.89)

Швидкість прямої реакції (в напрямку, показаному стрілкою) визначається середньою швидкістю проходження через бар’єр шириною  (рис. 4.34). За розподілом Максвелла знаходиvj за формулою

(4.90)

де m – маса молекули; Т – температура; k₀ – стала Больцмана. Середній час проходження через бар’єр становить:

(4.91)

За квантовою статистикою:

(4.92)

де h – стала Планка. Тоді

(4.93)

У загальному вигляді кінетичне рівняння для реакції (4.88) буде таким:

v = k[A][B], (4.94)

де k – константа швидкості реакції. Разом з тим швидкість реакції – це зміна концентрації за час  проходження через потенційний бар’єр

(4.95)

Порівнюючи (4.94) і (4.95) і підставивши  (4.93), отримуємо рівняння:

,

з якого знаходимо константу швидкості реакції k

. (4.96)

Після підстановки константи рівноваги К_р (4.89) маємо

. (4.97)

Відповідно до рівняння Вант-Гоффа (1.38),

де G⁰ – зміна стандартної вільної енергії хімічного перетворення. Тепер можна пов’язати k зі зміною термодинамічних величин, а саме:

. (4.98)

Оскільки G⁰ = H⁰ - TS⁰, тоді (4.98) буде таким:

(4.99)

Це рівняння Ейрінга.

Знайдемо зв’язок між Н й енергією активації E_a. Для цього прологарифмуємо, а далі знайдемо диференціал по Т від емпіричного рівняння Арреніуса (4.85):

,

(4.100)

і теоретичного рівняння (4.99)

,

. (4.101)

Порівнюючи (4.100) і (4.101), отримаємо:

E_a = H⁰ + RT.

Теплова енергія RT реагуючих молекул за Т = 300 К становить 2,5 кДж  моль^-1, тоді як енергії активації Е_а для багатьох хімічних реакцій досягають 100 кДж  моль^-1. Тому можна вважати, що у формулі Ейрінга (4.99) зміна ентальпії H⁰ з точністю до RT дорівнює енергії активації Е_а.

Термодинамічні величини Н⁰ і S⁰ надають інформацію про природу перехідного стану системи й вказують на те, що при активації молекул відбувається значна деформація хімічних зв’язків. Ентропія активації характеризує ймовірність утворення перехідного стану. Коли S⁰ є великою за значенням й від’ємною, і для утворення перехідного стану реагуючі молекули повинні мати точну просторову орієнтацію й певну конформацію, що для некаталітичних реакцій є мало ймовірно. Фермент значно змінює Н⁰ і S⁰, збільшуючи на багато порядків швидкість реакції.

Незважаючи на певні успіхи, теорія абсолютних швидкостей реакцій має низку обмежень. Зокрема, теорія перехідного стану постулює, що енергетичний бар’єр є статичним і його подолання відбувається тільки через енергію співударів атомів. Але білки характеризуються динамічністю своєї структури, й атомні групи постійно зміщуються на 0,05 нм. У щільно упакованій білковій глобулі рухомість атомних груп великого розміру поєднується з колективним зміщенням оточуючих груп. Рухома група співударяється з іншими групами, що створює ефект внутрішнього тертя й сповільнює швидкість переходу через енергетичний бар’єр. За теорією Крамерса (1940), яка базується на моделі руху через бар’єр під дією випадкової сили, постійна швидкості реакції становитиме:

, (4.102)

де  – в’язкість мікросередовища.