4.11. Кінетика ферментативних реакцій

Кінетика вивчає механізми й закономірності перебугу хімічних реакцій за часом залежно і від концентрації реагуючих речовин, і від умов їх перебігу (температури, тиску, рН тощо). Кількісною характеристикою, за якою описуються кінетичні процеси, є швидкість реакції v. Нехай відбувається проста хімічна реакція:

А + В  Р . (4.54)

Швидкість реакції v є зміна в часі концентрації продуктів реакції [Р]:

. (4.55)

Кінетичне рівняння для цієї реакції запишеться як

(4.56)

де k –константа швидкості реакції. Швидкість хімічної реакції, яка спостерігається на початку реакції, коли суттєві зміни концентрації реагуючих речовин не відбулися, називається початковою швидкістю хімічної реакці v₀; v₀ – це тангенс кута нахилу дотичної, проведеної з початку координат до експериментальної кривої [P] = f(t).

У загальному випадку швидкість реакції залежить від концентрації реагуючих речовин:

v = k[X]^m , (4.57)

де m – порядок реакції. Залежно від значення m реакції можуть мати різний порядок: реакція нульового порядку, m = 0 (швидкість не залежить від концентрації реагуючих речовин: v = k = const; реакція першого порядку, m = 1: v= k[X]; реакція другого порядку, m = 2 і т. д.

Для реакції (4.54) зменшення концентрації [A] проходить як реакція першого порядку

. (4.58)

Знайдемо, як змінюється із часом концентрація речовини А. Розділимо змінні в (4.58) й отримаємо диферинціальне рівняння першого порядку:

. (4.59)

Проінтегруємо (4.59) і отримаємо:

ln [A] – ln [A₀] = - k t, (4.60)

де [A₀] – початкова концентрація речовини А. Зміна із часом речовини А для реакції першого порядку буде такою:

[A] = [A₀]_e^-kt. (4.61)

Кінетичне рівняння (4.56) описує реакцію другого порядку. Реакції третього й більш високих порядків зустрічаються рідко.

Константа k є одією з важливих кінетичних характеристик. Вона відображає частоту активних співударів між молекулами реагуючих речовин. Розмірність k для реакції першого порядку становить [c^-1], другого – моль^-1·с^-1.

На початку ХХ ст. вивчалася кінетика ферментативних реакцій; зокрема, було досліджено реакцію гідролізу сахарози, яка каталізувалася дріжджовою інвертазою. Виявилося, що залежність початкової швидкісті ферментативної реакції v від концентрації субстрату [S], коли був надлишок субстрату над концентрацією фермента [E], описувалась гіперболою й не перевищувала певного максимального значення v_m. Ці факти було використаніо для створення першої теорії ферментативної реакції (Міхаеліс, Ментен, 1913). У цій теорії поступлювалося утворення коротживучого фермент-субстратного комплексу ES у простій реакції:

(4.62)

де E₁ – вільний фермент; Р – продукт реакції. Схематично таку взаємодію представлено на рис.4.29, а. Загальна концентрація ферменту [E] становитиме:

[E] = [E₁] + [ES]. (4.63)

Кінетичне рівняння швидкості утворення й розпаду фермент-субстратного комплексу можна записати таким чином:

. (4.64)

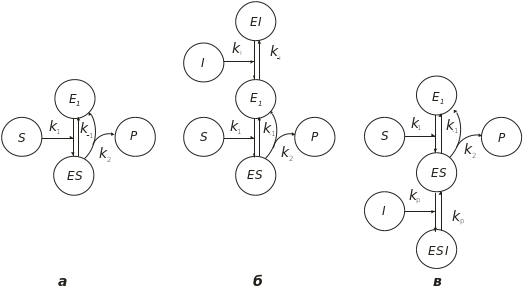
Рис. 4.29. Схема фермент-субстратної взаємодії:

а – без інгібіторів; б і в – за участю конкурентного й неконкурентного інгібіторів, відповідно; Е₁ – вільний фермент; S – субстрат; Р – продукт; І – інгібітор; k – константа швидкості реакції

Після запуску ферментативної реакції sз часом настає стаціонарний стан, в якому v₁ = 0. За умови стаціонарності з рівняння (4.64) з урахуванням v (4.63) знаходимо:

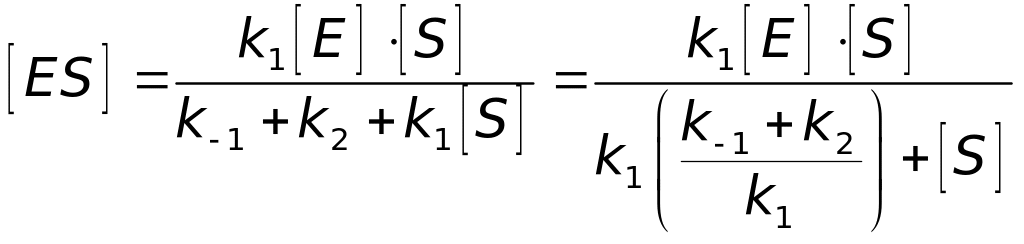. (4.65)

Відношення констант швидкості називається константою Міхаеліса:

(4.66)

Швидкість ферментативної реакції за рівнянням (4.62) і схемою (рис. 4.29, а) можна записати таким чином:

. (4.67)

Рівняння (4.67) може мати такий вигляд:

, (4.68)

де v_М = k₂[E]  максимальна швидкість ферментативної реакції. Рівняння (4.68) називається рівнянням Міхаєліса–Ментен. Залежність швидкості ферментативної реакції v від концентрації [S] представлено на рис. 4.30, а. За достатньо малих концентрацій субстрату ферментативна реакція відбувається як реакція першого порядку: . За великих концентрацій субстрату, коли , ферментативна реакція проходить як реакція нульового порядку: v = v_M. Як видно з рис. 4.30, а, константа Міхаеліса К_М відповідає такій концентрації субстрату, коли .

Для визначення двох важливих кінетичних характеристик К_M і v_M пропонується лінеаризувати рівнняння Міхаеліса–Ментен у такому вигляді:

. (4.69)

Відповідно до (4. 69), будується графік залежності 1/v від 1/[S] (графік Лайнуівера–Берка) (рис.4.30, б). З нахилу прямої отримуємо величину , а відрізок, який відсікається на jсі ординат, дорівнює 1/v_M.

Рис. 4.30. Кінетичні залежності фермент-субстратної взаємодії:

а – швидкості v від концентрації субстрату; v_max – максимальна швидкість ферментативної реакції; К_M – константа Міхаеліса; б – графік Лайнуівера–Берка; 1 – без інгібітора; 2 – з конкурентним інгібітором; 3 – з неконкурентним інгібітором

Параметр називається числом обертів прямої реакції. Для ферментативних реакцій число обертів змінюється в широких межах – від 10² до 10⁶ с^-1: для карбонатдегідрогенази , уреази k₂ = 10⁴ с^-1, карбоксипептидази k₂ = 10² с^-1. Це число визначає нижню межу константи швидкості реакції першого порядку, оскільки кожна елементарна стадія має відбуватися зі швидкістю не меншою, ніж максимальна швидкість загальної реакції. Величина, обернена числу обертів, визначає верхню межу часу життя будь-якої проміжної (інтермедіатної) форми ферменту. Якщо , тоді ферментний інтермедіат існує не більше 10^-2 c.

Речовини, які зменшують швидкість ферментативної реакції, називаються інгібіторами. Найпоширенішим типом інгібування є конкурентне інгібування. У цьому випадку інгібітор зв’язується з тим же самим активним центром ферменту, що й субстрат, утворюючи неактивний комплекс EI (рис. 4.29, б). За цим рисунком кінетичні рівняння будуть такими:

;

. (4.70)

Концентрацію загального ферменту можна записати таким чином:

. (4.71)

Використовуючи умову стаціонарності v₁ = 0 i v₂ = 0, із (4.70) і (4.71) знаходимо концентрацію [ES] за наявності конкурентного інгібітора:

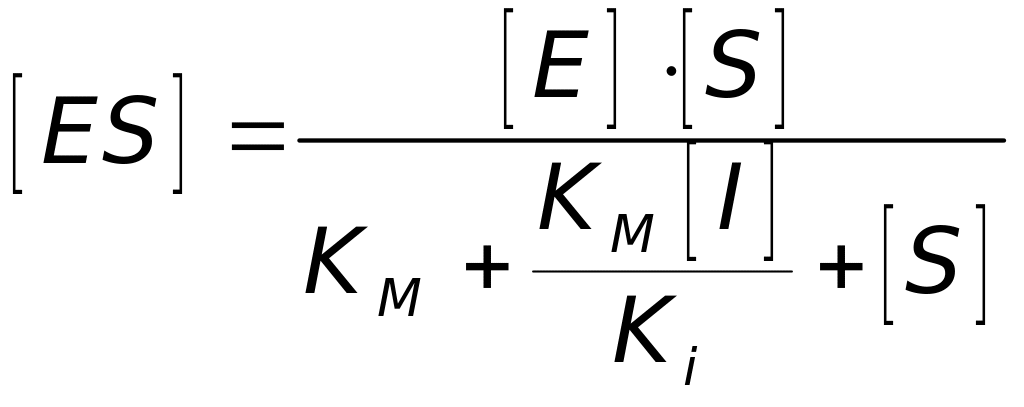, (4.72)

де – константа інгібування. Швидкість ферментативної реакції становитиме:

. (4.73)

На рис. 4.30, а представлена залежність v від [S] за наявності конкурентного інгібітора [I]. Видно, що конкурентний інгібітор не змінює v_M, але збільшує К_М, тому для досягнення максимальної швидкості необхідно значно збільшувати концентрацію сустрату. Рівняння (4.73) в координатах графіка Лайнуівера-Берка буде таким

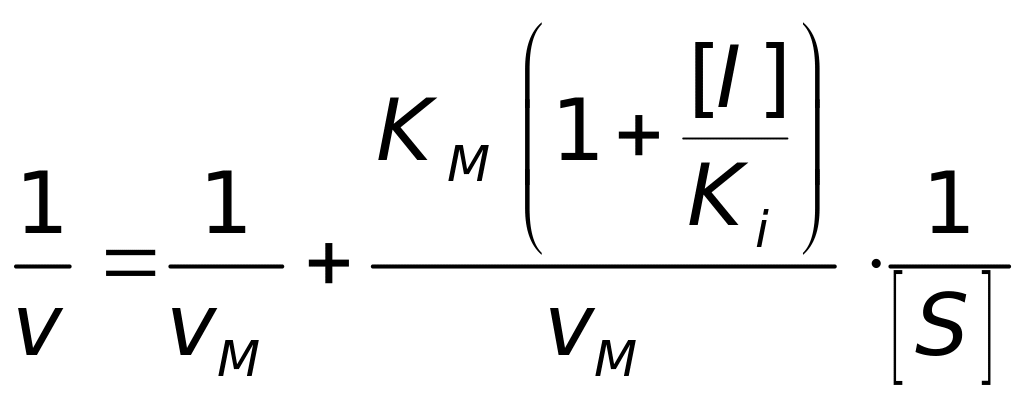. (4.74)

У присутності конкурентного інгібітора зростає нахил прямої й К_М збільшується в разів (рис. 4.30, б).

Неконкурентний інгібітор не зв’язується з активним центром, а зв’язується в іншому місці, й утворюється неактивний комплекс ESI (рис. 4.29, в). У цьому разі швидкість реакції визначається таким чином:

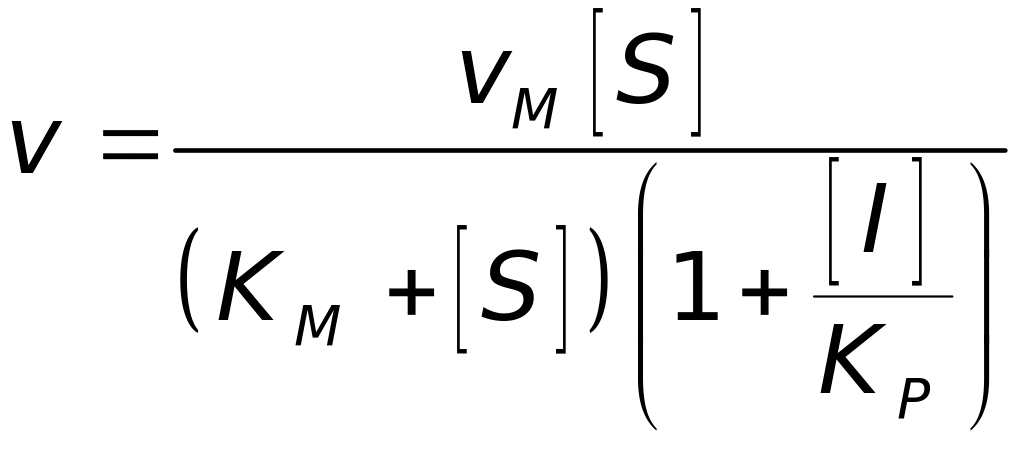, (4.75)

де – константа інгібування. Рівняння (4.75) у координатах графіка Лайнуівера–Берка буде таким:

. (4.76)

Неконкурентний інгібітор значно зменшує v_M (рис. 4.30, б).

Для визначення констант інгібування кінетичні залежності представляють у координатах графіка Діксона. Для конкурентного інгібітора:

, (4.77)

і неконкурентного інгібітора

. (4.78)

Будується графік залежності 1/v від [I] за двох фіксованих концентрацій субстрату [S] (рис. 4.31).

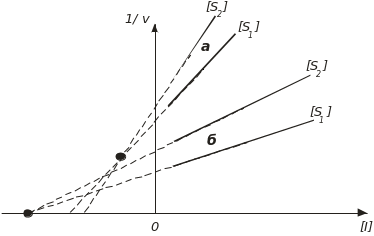
Рис. 4.31. Графік Діксона:

а і б – конкурентне й неконкурентне інгібування, відповідно; [S] і [І] – концентрація субстрату і інгібітора, відповідно

Із графіків Діксона легко визначаються константи інгібування К_і і К_р і тип інгібування. При неконкурентному інгібуванні прямі для різних [S] сходяться на осі абсцис в одній точці, якій відповідає константа інгібування К_р.

Методи дослідження нестаціонарної кінетики. Методи хімічного аналізу достатньо інерційні й дозволяють вивчати ферментативні реакції тільки в їх стаціонарній стадії. Значний інтерес становить дослідження реакцій на стадіях, які передують стаціонарному стану, тобто в передстаціонарному стані. Дослідження ферментативних реакцій у передстаціонарному режимі потребує спеціальної експериментальної техніки, оскільки мають реєструватися дуже швидкі стадії реакції, для чого необхідна достатньо висока роздільна здатність у часі. “Мертвий” час експериментальної методики повинен бути меншим за час перебігу реакції в передстаціонарному режимі. Час життя фермент-субстратних комплексів лежить у межах від 10^-2 до 10^-6 с. Це значить, що для дослідження передстаціонарної кінетики необхідні установки, які працюють у мілі- і мікросекундному інтервалі.

Широке застосування знайшов метод зупиненого струменя. У цьому методі використовується механічний пристрій для швидкого змішування ферменту із субстратом, що дозволяє реєструвати кінетичні криві в мілісекундному інтервалі. На рис. 4.32 наведено спрощену блок-схему установки для вивчення швидких реакцій.

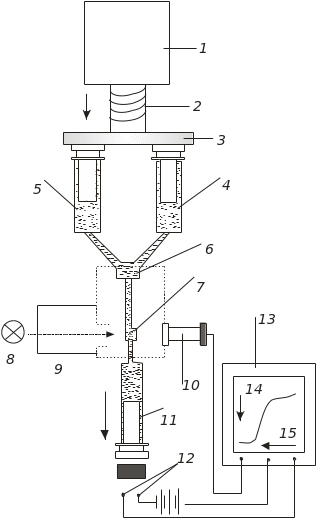
Рис. 4.32. Блок-схема приладу для вивчення кінетики ферментативних реакцій методом зупиненого струменя:

1 – мотор; 2 – шток; 3 – пластина вштовхування шпрців для розчину ферменту 4 і субстрату 5; 6 – камера змішування; 7– камера спостереження; 8 – джерело світла; 9 – монохроматор; 10 – ФЕП; 11 – шприц для зупинення потоку; 12 – тригерна контактна група; 13 – осцилограф; 14 – запуск установки; 15 – час зупинення потоку

Вирішальне значення має швидкість змішування ферменту із субстратом так, щоб час між змішуванням і заповненням камери спостереження мав бути значно коротшим за час передстаціонарної стадії. Безперервний перебіг реакції реєструється оптичною системою, яка включає джерело світла 8, монохроматор 9 і фотопомножувач (ФЕП) 10. Кінетика ферментативної реакції реєструється на екрані дисплея зразу ж після зупинки струменя. Швидка зупинка струменя проводиться шприцем 11 і тригерною контактною системою 12, за допомогою якої вимикається мотор. З моменту зупинки струменя тригерний механізм вмикає запис кінетики реакції. На змішування розчинів, заповнення камери спостереження, зупинку струменя й вмикання тригера витрачаються десяті частки мілісекунди.

Швидкі реакції у клітині, які відбуваються за участю ферментних і рецепторних білків, досліджуються методом імпульсного флеш-фотолізу. У цьому методі використовується лазер, який генерує дуже короткі (менше мікросекунди) імпульси УФ-світла ( = 330–360 нм) і освітлює ними розчин ферменту чи суспензію клітин. Ферментативна реакція запускається дією потужного світлового спалаху (флеш) лазера, й оптичний прилад реєструє швидку кінетику. Значні успіхи в цьому методі досягнуто завдяки використанню специфічних речовин, які дістали назву кейджед-зонди (англ. сaged – ув’язнений). Ці зонди легко проникають у клітину, але там вони біологічно неактивні, тому що їхні реактивні групи хімічно екрановані певними атомними групами. Після дії спалаху УФ-світла розривається хімічний зв’язок екрануючої групи, і кейджед-зонд перетворюється на активний субстрат ферментативної реакції.

Зараз синтезовані різні кейджед-зонди. Кейджед-АТФ (NPE-caged ATP, NMNPE-caged ATP) використовується для дослідження у клітині роботи міозинової АТФази м’яза, Na⁺-K⁺- i Ca²⁺-насосу мембран, кейдж-іонофори (ДМNPE-caged A-23187, ДМNPE-caged BrA-23187)  транспорту іонів Са²⁺ через плазматичну мембрану або звільнення Са²⁺ з внутрішньомолекулярних депо. Широко використовуються вторинні месенджери: кейдж-цАМФ (NPE-caged АМР) і кейдж-Са²⁺ (NP-EGTA i ДМ –нітрофен). Спорідненість NP-EGTA до Са²⁺ зменшується в 12 500 разів після фотолізу (константа дисоціації K_d = 80 нмоль/л до спалаху УФ-світла зростає до К_d = 1 ммоль/л після спалаху) (рис. 4.33), і звільнені іони Са²⁺ дуже швидко включаються у функцію починають виконувати функцію вторинних посередників у внутрішньоклітинних процесах.

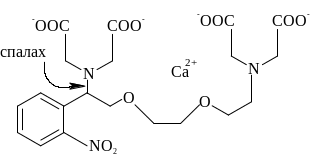
Рис. 4.33. Фотодисоціація caged-Ca²⁺ (NP-EGTA) через спалах УФ-світла

Для аналізу механізму ферментативних реакцій широко використовуються методи релаксаційної кінетики, які базуються на тому, що через швидке зовнішнє збурення системи (зміна температури, тиску, електричного поля) для досягнення нової рівноваги потрібен певний час. Перехід системи до нових рівноважних концентрацій реагуючих речовин називається хімічною релаксацією.

Нехай досліджується реакція (4.62). На початку за температури Т₀ система перебуває в рівновазі, яка характеризується рівноважними концентраціями і константою рівноваги К₀. Припустимо, що в системі різко змінюється температура Т = Т₀ + Т. Це спричиняє зміну константи рівноваги К = К₀ + К і рівноважних концентрацій:

. (4.79)

Кінетичне рівняння запишеться як:

,

а з урахуванням (4.79) матиме такий вигляд:

.

У стані рівноваги , і при температурному збуренні відхилення від рівноваги є настільки незначним, що , крім того, зберігається баланс по масі реагуючих компонент, коли , тоді

(4.80)

Це неоднорідне диференційне рівняння відносно [ES]. Розв’язок рівняння (4.80) дає зміну за часом концентрації фермент-субстратного комплексу до досягнення нової рівноваги:

(4.81)

де [ES]_M max – максимальна зміна концентрації фермент-субстратного комплексу при досягненні нової рівноваги. Час, коли [ES] зростає на 63,2 %, називається часом релаксації системи:

(4.82)

Дослідження релаксаційної кінетики і вимірювання часу релаксації проводиться за допомогою методу температурного стрибка. У цьому методі швидка зміна температури Т забезпечується діює розряду високовольтного конденсатора в невеликій за об’ємом реакційній камері (0,1 мл). Це дозволяє за мікросекунди підвищити температуру на 10⁰ і після цього досліджувати, як ферментативна система релаксує до нового рівноважного стану. Оптична система реєструє невеликі зміни в часі концентрацій проміжних реагентів, що дозволяє знайти кінетичні параметри системи. Якщо за методом зупиненого струменя реєструються кінетичні характеристики в мілісекундному інтервалі, то за допомогою методу температурного стрибка досліджується кінетика в мікросекундному інтервалі.

Використання швидких методів реєстрації засвідчило, що на відміну від простих моделей взаємодії ферменту із субстратом за схемою (4.62), коли вивчаються тільки стаціонарні стани реакції, в реальних ситуаціях існує велика кількість швидких проміжних стадій ферментативних реакцій:

, (4.83)

де – проміжні конформації (інтермедіати) ферменту.