Тема 7 індекси

Індекс – це відносна величина, яка характеризує зміну явища в часі, просторі чи порівняно з певним стандартом (нормативом). Залежно від характеру порівнянь індекси поділяють на динамічні, територіальні та досягнення певного стандарту.

За ступенем охоплення елементів сукупності, тобто за агрегованістю інформації, індекси поділяються на індивідуальні та зведені. Індuвідуальні індекси характеризують зміну в часі чи співвідношення у просторі одного якогось індивідуального явища. Зведені індекси являють собою співвідношення рівнів складного явища, до якого входять різнорідні елементи.

Якщо вивчається відносна зміна якогось показника по сукупності, поділеній на групи, то зведений індекс може бути груповим (субіндексом) або загальним.

Зведені індекси як узагальнені характеристики дають змогу не лише вивчати зміну якогось агрегованого показника в часі чи просторі, а й кількісно оцінювати вплив окремих факторів, тобто вони виконують як синтетичну, так і аналітичну функцію.

За формою індекси поділяються на агрегатні, середньозважені та індекси середніх величин. Вибір того чи іншого індексу залежить від мети дослідження, економічної суті показника, що вивчається, та наявної інформації.

Будь-який індекс – це співвідношення двох однойменних показників. Той, з яким здійснюється порівняння, називають базою порівняння. Так, в індексах динаміки базою порівняння є показник якогось попереднього періоду (моменту) часу, у територіальних індексах – показник певного регіону (об'єкта).

Застосовуючи індексний метод, дотримуються відповідних умовних позначень, загальноприйнятих у теорії та практиці статистики. Основні з них:

q – кількість проданого товару чи обсяг виробленої продукції певного виду в натуральному виразі;

р – ціна одиниці товару чи продукції;

z – собівартість одиниці продукції;

t – затрати робочого часу на одиницю продукції (трудомісткість) і т. ін.

Виходячи з цих позначень, можна записати:

pq – вартість товару певного виду (товарооборот) або вартість виготовленої продукції;

zq – грошові витрати на виробництво;

tq – затрати робочого часу на виробництво і т. ін.

Показники базисного періоду мають у формулах підрядковий знак «0», а поточні – «1». Показник, зміна якого вивчається, називається індексованим. Підрядковий знак самого індексу вказує на індексовану величину.

Наприклад, індивідуальні індекси:

іq = q1 / q0 – індекс фізичного обсягу товару (виготовленої продукції);

іp = p1 / p0 – індекс ціни;

іpq = p1q1 / p0q0 – індекс вартості (товарообороту) конкретного виду продукції.

Індивідуальні індекси, що характеризують зміну явищ, поєднаних між собою як співмножники, мають такий взаємозв'язок: добуток індексів співмножників дорівнює індексу добутку. Наприклад, індекс товарообороту дорівнює добутку індексу ціни та індексу фізичного обсягу (i_pq = іріq). Такі індекси мають назву сполучених, спряжених, співзалежних. Взаємопов'язані також індекси прямих і обернених показників.

Соціально-економічні явища й ті показники, що їх характеризують, можуть бути порівнянними, якщо вони мають якусь спільну міру, і не порівнянними. Так, не можна безпосередньо додавати фізичний обсяг товарів, які мають різні одиниці виміру (кг, м, мг тощо) та різну споживчу вартість. При агрегуванні таких елементів їх фізичні обсяги q зводяться до порівнянного (зіставного) вигляду за допомогою таких сумірників, як ціна, собівартість чи трудомісткість одиниці продукції. Перемноживши, наприклад, ціни на відповідну кількість проданих товарів і додавши добутки, дістанемо загальний товарооборот. Відносну його зміну в динаміці характеризує зведений індекс товарообороту у фактичних цінах:

Jpq = Ʃp1q1 / Ʃp0q0.

Формули індексів загальних витрат (грошових та трудових) на виробництво продукції мають такий вигляд:

Jzq = Ʃz1q1 / Ʃz0q0; Jtq = Ʃt1q1 / Ʃt0q0.

Кожний із поданих зведених індексів характеризує зміну показника, що являє собою результат добутку двох факторів-співмножників. Очевидно, що зміна такого показника зумовлюється зміною кожного з цих факторів зокрема.

Так, зміна товарообороту у фактичних цінах може бути викликана як зниженням чи підвищенням цін на окремі товари, так і зміною кількості (фізичного) обсягу реалізованих товарів. Щоб виявити окремий вплив якогось одного з цих факторів-співмножників на зміну товарообороту в поточному періоді порівняно з базисним, слід інший умовно вважати незмінним, тобто зафіксувати на рівні одного періоду. Кожний з незмінних співмножників при побудові індексів відіграє властиву йому роль. Якщо незмінним є екстенсивний показник, то він відіграє роль статистичної ваги, а якщо інтенсивний – то він використовується як сумірник. Таке розмежування показників необхідне лише при побудові зведених індексів і саме тоді, коли індекс має характеризувати зміну якогось агрегату за рахунок окремого фактора.

Так, в індексі цін індексується, тобто змінюється саме ціна кожного з проданих товарів (інтенсивний показник), а кількість реалізованих товарів (екстенсивний показник) фіксується на рівні одного й того самого періоду; а в індексі фізичного обсягу індексується кількість проданих товарів і фіксується ціна. Кожен із факторів-співмножників можна фіксувати на рівні як базисного, так і поточного періоду.

Далі при побудові зведених індексів застосуємо таку систему зважування: інтенсивні показники (сумірники) фіксуємо на рівні базисного періоду, а екстенсивні (ваги) – на рівні поточного періоду. За цих умов відносну зміну товарообороту у фактичних цінах за рахунок зміни цін та за рахунок зміни фізичного обсягу характеризуватимуть відповідно такі індекси:

Jp = Ʃp1q1 / Ʃp0q1; Jq = Ʃp0q1 / Ʃp0q0.

Індекси факторів-співмножників та індекс агрегованого результативного показника мультиплікативно пов'язані між собою: Jpq = Jp * Jq. Знаючи будь-які два індекси цієї системи, можна визначити третій. Цей зв'язок забезпечується тоді, коли один з індексів-співмножників обчислюється за поточною вагою, а другий – за базисним сумірником або навпаки.

Індексна система співзалежних (спряжених) індексів дає змогу оцінити не лише відносний, а й абсолютний вплив факторів-співмножників на результативний показник. Абсолютний приріст на підставі індексів визначається як різниця між чисельником і знаменником відповідного індексу.

Абсолютний приріст товарообороту у фактичних цінах:

Δpq = Ʃp1q1 – Ʃp0q0,

у тому числі за рахунок зміни:

цін:

Δp = Ʃp1q1 – Ʃp0q1;

фізичного обсягу:

Δq = Ʃp0q1 – Ʃp0q0.

Очевидно, що

Δpq = Δp + Δq.

Подані формули зведених індексів називають агрегатними.

В окремих випадках виникає потреба у використанні середньозважених індексів, тотожних агрегатній їх формі. Якщо, скажімо, за низкою реалізованих товарів відомі індивідуальні індекси ціни іp та товарооборот поточного періоду, то зведений індекс цін за таких умов визначають за формулою середньозваженого гармонійного індексу:

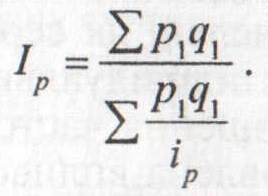
Цей індекс тотожний зведеному агрегатному індексу, що випливає з таких перетворень:

Зведений індекс фізичного обсягу на підставі індивідуальних індексів іq та товарообороту базисного періоду визначається за формулою середньозваженого арифметичного індексу:

Шляхом аналогічних перетворень легко довести тотожність цього індексу агрегатній його формі:

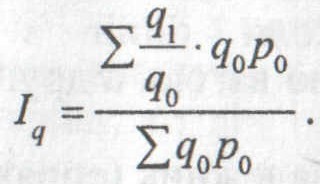
У статистико-економічному аналізі нерідко доводиться порівнювати такі узагальнюючі характеристики, як середня ціна, середня собівартість, середня кредитна ставка тощо. У даному разі йдеться про середні, що обчислені як середньозважені. Рівень такої середньої залежить як від індивідуальних значень осереднюваної ознаки, так і від співвідношення частот (ваг). Тому і зміна такої середньої в динаміці зумовлена впливом тих самих факторів, від яких залежить сама середня. Аналіз динаміки середнього рівня будь-якого інтенсивного показника здійснюють за допомогою таких взаємозв'язаних індексів: змінного складу фіксованого складу та структурних зрушень .

Індекс змінного складу характеризує відносну зміну середнього рівня в цілому за рахунок обох факторів:

Індекс фіксованого складу характеризує зміну середнього рівня за рахунок лише значень ознаки, тобто варіант, за незмінної структури сукупності:

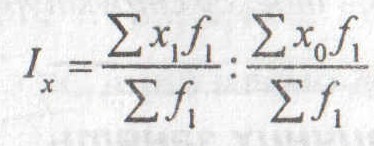
Індекс структурних зрушень характеризує зміну середнього рівня за рахунок змін, що відбулись у структурі сукупності:

Між індексами середніх величин існує такий взаємозв'язок:

ТЕРМІНОЛОГІЧНИЙ СЛОВНИК

Динамічний індекс – характеризує зміну явища в часі.

Територіальний індекс – оцінює результат порівняння явища у просторі (за різними об'єктами, регіонами).

Індексована величина – показник, відносна зміна якого вивчається в часі чи просторі.

Інтенсивний показник – один з факторів співмножників, що відбиває певною мірою його якісну суть.

Екстенсивний показник – один із факторів співмножників, що відбиває суто обсягову його характеристику.

Сумірник – показник, який дає змогу звести до порівнянного вигляду сукупність різнорідних елементів.

ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. У чому полягає суть індексу?

2. Назвіть критерй; за якими класифікуються індекси.

3. Чим відрізняється зведений індекс від індивідуального?

4. Які з показників, як правило, відіграють роль сумірників?

5. Поясніть аналітичну функцію систем спряжених індексів.

6. Як визначuти абсолютний приріст результативного показника за рахунок окремих факторів-співмножників?

7. За яких умов застосовуються середньозважені індекси?

8. Чим відрізняються індекси змінного та фіксованого складу?

9. Поясніть економічну сутність індексу структурних зрушень.