Тема 5 середні величини та показники варіації

Середня величина – це узагальнююча міра варіювальної ознаки, що характеризує її рівень в розрахунку на одиницю сукупності. Умовами застосування середніх величин наявність якісно однорідної сукупності та достатньо великий її обсяг.

У статистичній практиці використовують кілька видів середніх: середню арифметичну, середню гармонічну, середню геометричну, середню квадратичну і т. ін. Кожна із зазначених середніх може набирати двох форм: простої і зваженої. Проста застосовується в разі обчислення середньої за первинними (незгрупованими) даними, а зважена – за вторинними (згрупованими) даними.

Використання того чи іншого виду середніх залежить від двох обставин. По-перше, від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні). По-друге, від характеру алгебраїчного зв'язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, ступінь, квадратичний корінь). Цей зв'язок є визначальною властивістю сукупності і відбивається в логічній формулі осереднювальної ознаки. На підставі логічної формули обирається вид середньої.

Середня арифметична застосовується для осереднення прямих значень ознак їх підсумуванням. Логічна формула середньої арифметичної має вигляд:

Чисельник цієї формули середньої являє собою визначальну властивість, яка є реальною абсолютною чи відносною величиною і має самостійне значення в аналізі.

Якщо дані не згруповані, використовується середня арифметична проста

де х – окремі значення ознаки; п – обсяг сукупності.

За формулою середньої арифметичної простої обчислюються також середні у хронологічному ряду, якщо інтервали часу, за який подаються значення ознак, рівні.

Якщо у хронологічному ряду наведено моментні показники, то для обчислення середньої вони замінюються півсумами значень на початок і кінець періоду. Якщо моментів більш ніж два і інтервали між ними рівні, то середня обчислюється за формулою середньої хронологічної:

де п – кількість моментів.

У великих за обсягом сукупностях окремі значення ознаки – варіанти можуть повторюватись. У такому разі їх можна об’єднати у групи (j = 1,2,...,m), а обсяг значень ознаки визначити як суму добутків варіант xj на відповідні їм частоти fj, тобто як . Такий процес множення у статистиці називають зважуванням, а кількість елементів сукупності з однаковими варіантами – вагами. Значення ознаки осереднюються за формулою середньої арифметичної зваженої

Вагами можуть бути частоти або частки (відносні величини структури) dj:

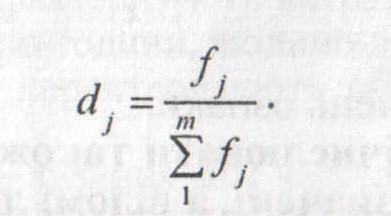
У структурованій сукупності під час розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні , кожна з яких має відповідну вагу у вигляді групових частот fj:

Обчислену так середню називають загальною.

Вагою може бути також абсолютна величина, яка логічно пов'язана з осереднюваним показником. Ваги вибирають за допомогою логічної формули показника. Оскільки середня величина обчислюється з розрахунку на одиницю сукупності, то вага завжди міститься у знаменнику логічної формули.

Користуються таким практичним правилом: за наявності інформації про значення знаменника логічної формули (ваги) застовується середня арифметична зважена. За відсутності даних про ваги беруть середню гармонічну зважену.

Середня гармонічна застосовується для обчислення середньої з обернених показників їх підсумуванням. Для незгрупованих даних береться середня гармонічна проста

Якщо дані згруповані, то використовується середня гармонічна зважена

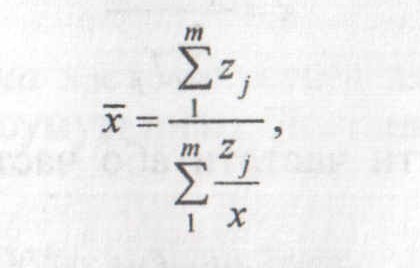
де zj = xj fj – обсяг значень ознаки.

Середню можна обчислювати також тоді, коли окремі значення варіантів не зазначені, а відомі лише підсумки (сумарні значення чисельника та знаменника) логічної формули.

Середня геометрична визначається як добуток відносних величин динаміки xі, що є кратним відношенням і-го значення показника до попереднього (і-1)-го. Формула середньої геометричної простої:

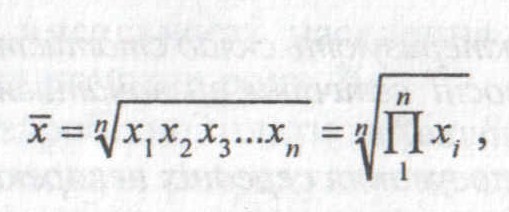
де П – символ добутку; xі – відносні величини динаміки, виражені кратним відношенням і-го значення показника до попереднього (і-1)-го.

Якщо часові інтервали різні, використовують середню геометричну зважену:

де nj – часовий інтервал, Ʃnj = n.

Ряд розподілу характеризує склад і структуру сукупності за певною ознакою. Він утворюється з двох елементів: варіант – значень групувальної ознаки хj та частот (часток) fj. Співвідношенням варіант і частот подається закономірність розподілу.

Залежно від статистичної природи варіант ряди розподілу поділяються на атрибутивні та варіаційні. Частотними характеристиками будь-якого ряду є абсолютна чисельність j-ї групи – частота fj, відносна частота j-ї групи – частка dj, для варіаційних рядів також кумулятивна частота Sjі – частка Sdі.

Звідси, , або 100 %. Кумулятивні характеристики визначаються послідовним об'єднанням груп і підсумовуванням відповідних їм частот (часток).

Аналіз закономірностей розподілу грунтується на характеристиках: а) центру розподілу; б) варіації; в) форми розподілу (асиметрії, концентрації).

До характеристик центру розподілу відносять середню, моду та медіану. Середня величина характеризує типовий рівень ознаки в сукупності. За даними ряду розподілу середня обчислюється як арифметична зважена, де вагами є частоти fj або частки dj:

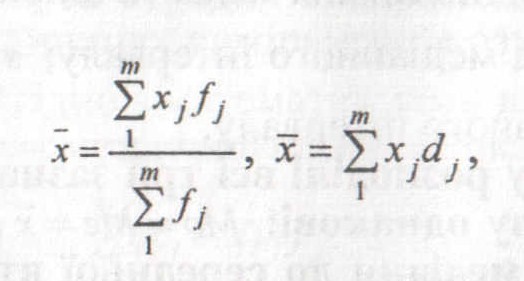
де j – номер групи; т – кількість груп.

В інтервальних рядах, припускаючи рівномірний розподіл елементів сукупності в межах j-гo інтервалу, за варіанту хj беруть середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою самою, як і сусіднього закритого інтервалу.

Модою (Мо) називають найпоширеніше значення ознаки. У дискретному ряді її визначають візуально за найбільшою частотою (часткою). В інтервальному ряді за таким принципом знаходять модальний інтервал, всередині якого конкретне модальне значення обчислюють за інтерполяційною формулою:

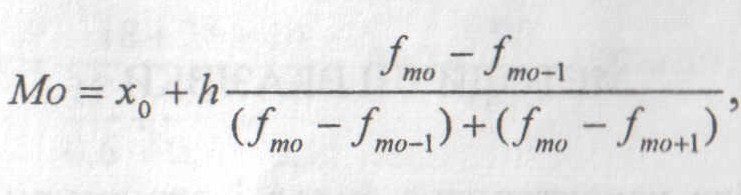
де х0 та h – відповідно нижня межа та ширина модального інтервалу; fmo, fmo-1, fmo+1 – частота (частка) відповідно модального, передмодального та післямодального інтервалу.

Медіана (Ме) – це таке значення ознаки, що варіює, яке припадає на середину впорядкованого ряду, поділяючи його на дві рівні за обсягом частини. Для визначення медіани використовують кумулятивні частоти Sfj або частки Sdj. У дискретному ряді медіаною є значення ознаки, кумулятивна частота якої перевищує половину обсягу сукупності, тобто (для кумулятивної частки Sdj ≥ 0,5). В інтервальному ряді за цим принципом визначають медіанний інтервал, а значення медіани всередині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:

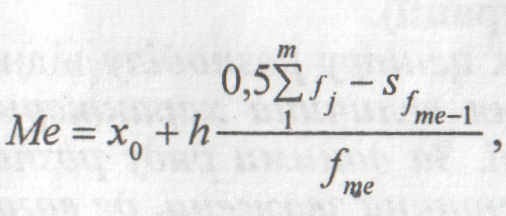
де х_о та h – відповідно нижня межа та ширина медіанного інтервалу; fme – частота медіанного інтервалу; Sfme-1 – кумулятивна частота передмедіанного інтервалу.

У симетричному розподілі всі три зазначені характеристики центра розподілу однакові: , у помірно асиметричному відстань медіани до середньої втричі менша за відстань середньої до моди, тобто .

В одних сукупностях індивідуальні значення ознаки щільно групуються навколо центра розподілу, в інших – значно відхиляються, варіюють. Чим менша варіація, тим однорідніша сукупність, більш надійні й типові характеристики центра розподілу, передусім середня величина. Для вимірювання та оцінювання варіації використовують абсолютні та відносні характеристики.

Найпростішою з таких характеристик є варіаційний розмах R, що характеризує діапазон варіації і визначається як різниця між максимальним і мінімальним значеннями ознаки:

Більшість характеристик варіації визначають, усереднюючи відхилення індивідуальних значень ознаки від центра розподілу, поданого середньою величиною. Оскільки алгебраїчна сума відхилень дорівнює нулю , то усереднюються модулі або квадрати відхилень. Середній з модулів відхилень називають середнім лінійним відхиленням , середній квадрат відхилень – дисперсією , корінь квадратний з дисперсії – середнім квадратичним відхиленням Ϭ:

За первинними, незгрупованими даними наведені характеристики обчислюють за принципом незваженої середньої:

Середнє лінійне та середнє квадратичне Ϭ відхилення – іменовані числа (в одиницях вимірювання ознаки), за змістом вони ідентичні, проте згідно з математичними властивостями Ϭ > .

Дисперсію для ознак метричної шкали обчислюють за формулою:

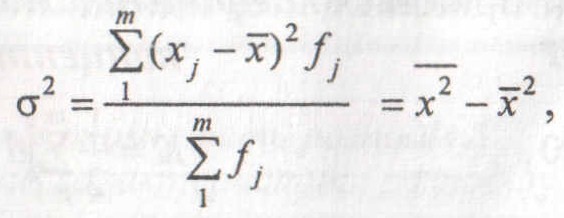
де – середній квадрат значень ознаки; – квадрат середньої величини.

Дисперсія альтернативної ознаки обчислюється як добуток·часток: = d1d0, де d1 – частка елементів сукупності, яким притаманна ознака, d0 – частка решти елементів (d0 = 1 – d1).

Порівнюючи варіації різних ознак або однієї ознаки в різних сукупностях, використовують коефіцієнти варіації V. Вони визначаються відношенням абсолютних іменованих характеристик варіації до центра розподілу і найчастіше виражаються у процентах. Отже, маємо коефіцієнти варіації:

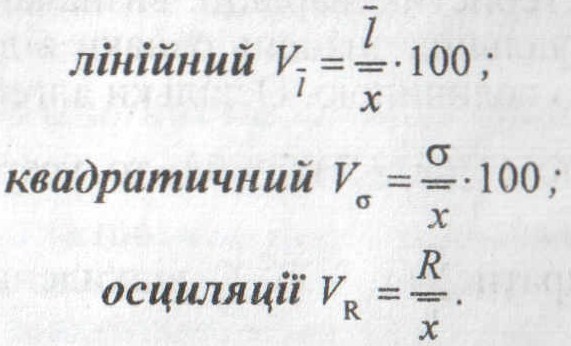
Аналіз закономірностей розподілу передбачає оцінку ступеня однорідності сукупності та симетричності розподілу. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації, значення якого в симетричному розподілі становить VϬ = 0,33.

Найпростішою мірою асиметричності розподілу є відхилення між характеристиками центра розподілу. Чим помітніша асиметрія, тим більше відхилення . Стандартизоване відхилення називають коефіцієнтом асиметрії . У разі правосторонньої асиметрії А > О, у разі лівосторонньої – А < О.

Оцінка нерівномірності розподілу між окремими складовими сукупності гpунтується на порівнянні часток двох розподілів - за кількістю елементів сукупності d_J і обсягом значень ознаки D_J. Якщо розподіл значень ознаки в сукупності рівномірний, то d_J = D_J, а відхилення часток свідчать про певну неоднорідність, яка вимірюється коефіцієнтами:

Коефіцієнт локалізації визначається для кожної складової сукупності, коефіцієнт концентрації є узагальнюючою для сукупності характеристикою відхилення розподілу від рівномірного.

Порівняння структур на основі відхилень часток – ефективний спосіб вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та атрибутивних рядів. У разі рівномірного розподілу всі значення L_j = 1, а К = 0. Чим помітніша диференціація, тим більше значення цих коефіцієнтів відхиляються, відповідно, від 1 та 0.

Структура будь-якої статистичної сукупності динамічна. Зміна часток окремих складових сукупності свідчить про структурні зрушення. Мірою інтенсивності структурних зрушень (у процентних пунктах – п. п.) є середнє лінійне або середнє квадратичне відхилення часток:

де dj0 та dj1 – частки відповідно базисного та поточного періодів; т – кількість складових сукупності.

ТЕРМІНОЛОГІЧНИЙ СЛОВНИК

Логічна формула середньої арифметичної – словесна формула; що розкриває сутність осереднювальної ознаки та відбиває характер алгебраїчного зв'язку між індивідуальними значеннями ознаки та її загальним обсягом.

Кумулятивна частота (частка) характеризує обсяг сукупності зі значеннями варіант, які не перевищують хj.

Абсолютні міри варіації: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії.

Відносні міри варіації: коефіцієнти варіації, локалізації, концентрації.

Однорідна сукупність – це така сукупність, елементи якої мають спільні властивості і належать до одного типу. В однорідних сукупностях розподіли одновершинні (одномодальні).

ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. За яких умов застосування середніх некоректне?

2. Які види середніх використовуються за відсутності інформації про ваги або в разі, коли замість окремих значень осереднювальної ознаки наведено лише сумарні значення складових логічної формули?

3. Як виявляється закономірність розподілу?

4. Назвіть частотні характеристики розподілу їх особливості.

5. Поясніть сутність характеристик центра розподілу. Як вони співвідносяться?

6. Середня величина ознаки у двох сукупностях однакова. Чи може бути різною варіація цієї ознаки?

7. Поясніть сутність середнього лінійного і середнього квадратичного відхилень. Чи ідентичні вони за змістом і чи однакові за значенням?

8. Як порівняти варіацію різних ознак або однієї ознаки в різних сукупностях?

9. На яких засадах грунтується оцінка нерівномірностізподілу? Поясніть зміст і особливості розрахунку коефіцієнтів локалізації та концентрації.

10. Які характеристики варіації застосовують для оцінювання інтенсивності структурних зрушень?