3.3.4 Интервальные оценки случайной величины (результатов измерений)

В общем случае определение СКО не является лучшим способом оценки погрешностей. Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Чаще всего его используют на потому, что это единственная оценка, легко рассчитываемая в аналитическом виде. Принимая точечную оценку   за истинное значение измеряемой величины, надо убедиться в ее точности. В качестве меры точности рассматривают интервальную оценку – симметричный интервал (-ΔX1,+ ΔX2 ), между границами которого с заданной доверительной вероятностью находится истинное значение измеряемой величины.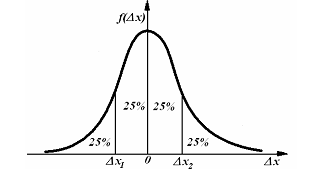

Интервальная оценка - оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется доверительным интервалом, а задаваемая исследователем вероятность называется доверительной вероятностью.  В практике статистических вычислений применяются стандартные значения доверительной вероятности: 0,95, 0,98 и 0,99 (95%, 98% и 99% соответственно). Очевидно, что чем выше доверительная вероятность, тем выше точность оценки, но шире доверительный интервал. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений.

Квантильные оценки распределения случайных погрешностей

При таких оценках исходят из того, что площадь, заключенная под кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы этих линий называют квантилями. Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. Абсцисса (-Δ1) есть 25%-ная квантиль, так как площадь под кривой р(Δ) слева от нее составляет 25 % всей площади. Абсцисса (+Δ1) соответствует 75%-ной квантили. На практике 25%- и 75%-ный квантили принято называть сгибами, или квантилями распределения.  Между ними заключено 50 % всех возможных значений случайной погрешности измерений. Интервал значений случайной погрешности между Δ=005 и Δ=0,95 охватывает 90 % всех возможных значений.

Для получения интервальной оценки нормально распределенной случайной величины необходимо:

• определить точечную оценку МО х и СКО S_x случайной величины;

• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

• найти верхнюю Xmin и нижнюю Xmax границы;

Xmin = X - T(ν,P) Xmax = X + T(ν,P)

где: Xmin, Xmax - нижняя и верхняя границы интервала;    X - среднее арифметическое (точечная оценка МО);      n - объем выборки;      T(ν,P) - поправочный коэффициент, называемый T-статистика, величина которого определяется значением задаваемой доверительной вероятности P и числом степеней свободы ν ;

     - оценка СКО случайной величины X.

На графике нормального распределения погрешностей по оси абсцисс отложены интервалы с границами ±σ, ±2σ, ±3σ, ±4σ. Доверительные вероятности для этих интервалов приведены в таблице.

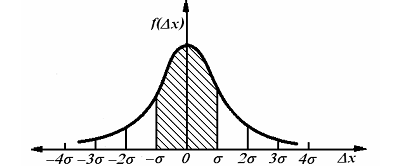
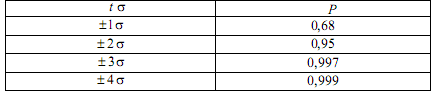
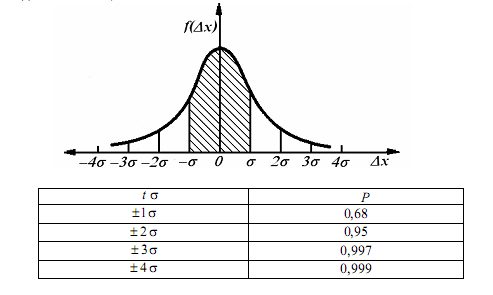
Как видно из этой таблицы, оценка случайной погрешности группы наблюдений интервалом ±1σ соответствует доверительной вероятности 0,68. Такая оценка не дает уверенности в высоком качестве измерений, поскольку 32% от всего числа наблюдений может выйти за пределы указанного интервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3σ соответствует Ρ = 0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.

В целях единообразия в оценивании случайных погрешностей интервальными оценками при технических измерениях доверительная вероятность принимается равной 0,95. Лишь для особо точных и ответственных измерений (важных, например, для безопасности и здоровья людей) допускается применять более высокую доверительную вероятность.