3) Визначити статус ресурсів, що використовуються для виробництва продукції, та рентабельність кожного виду продукції
Праві частини системи обмежень вважатимемо ресурсами Ri (i = 1 .. 5) – відповідно потужність заводу, коштів для доставки до Києва та значення попиту в інших містах, оптимальне використання яких максимізує цільову функцію.
Проаналізуємо одержані результати. За даного плану виробництва невикористаним залишається 10 од. ресурсів R5 – тобто потреби Яготина, куди масло реалізувати невигідно через низьку ціну.
Розв'язок двоїстої задачі виписуємо з 6 рядка останньої симплекс-таблиці, де y1 = x5, y2 = x6, y3 = x7, y4 = x8, y5 = x9, тобто y1 = 40, y2 = 20, y3 = 40, y4 = 0, y5 = 0.
Змінні y1, y2, y3 означають умовні двоїсті одиниці ресурсів відповідно 1, 2, 3 виду. Двоїста оцінка 4 та 5 ресурсу рівна 0. Ці ресурси не повністю використовуються при оптимальному плані виробництва, тому є недефіцитними – тобто попит Харкова та Яготина.
Оцінка рентабельності продукції, що постачається в міста, виконується за допомогою двоїстих оцінок та обмежень двоїстої задачі, що характеризують кожний вид поставок. Підставимо Y = (40, 20, 40, 0, 0) у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то доставка в таке місто для заводу недоцільне. Якщо співвідношення виконується як рівняння, то доставка рентабельна.
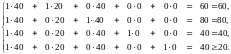
Аналогічні результати можна дістати, проаналізувавши двоїсті оцінки додаткових змінних, значення яких показують, на скільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо y ≠ 0, то відповідна доставка нерентабельна. Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс-таблиці у стовпчиках "x1" – "x4". Отже, доставка в перші три міста – рентабельна – їх оптимальні значення рівні x1 = 0, x2 = 0, x3 = 0. Оскільки x4 = 20, тому доставка по Яготину – нерентабельна.
4) Інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів
За знайденим розв'язком задачі проведемо аналіз стійкості двоїстих оцінок [АКУ, c.100] відносно змінної bi. Це, в свою чергу, дасть змогу проаналізувати стійкість оптимального плану задачі відносно зміни вільних членів, оцінити ступінь впливу зміни граничного значення ресурсу певного виду на максимальне значення цільової функції. Також дає можливість визначити найбільш доцільний варіант можливих змін bi. Для цього знайдемо компоненти вектора b*:
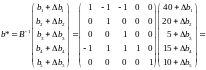
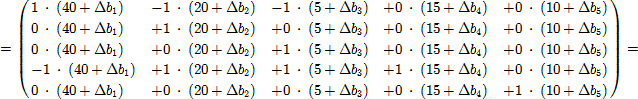
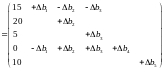
Тут матриця B–1 відповідає виділеному фрагменту останньої симплекс-таблиці. Умова невід'ємності компонент вказаного вище вектора задає систему нерівностей:
Якщо Δb2 = 0, Δb3 = 0, Δb4 = 0, Δb5 = 0, то:
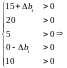
і інтервал зміни Δb1 наступний: –15 < Δb1 < 0, звідки 25 < b1 < 40.
Це означає, що якщо кількість ресурсів 1 типу буде змінено в знайдених межах, то, незважаючи на це, оптимальним планом двоїстої задачі залишиться Y = (40, 20, 40, 0, 0).
Згідно з цим, максимально можливий дохід підприємства перебуватиме в межах:
2200 –15 · 40 < zmax < 2200 +0 · 40
1600 < zmax < 2200
Якщо Δb1 = 0, Δb3 = 0, Δb4 = 0, Δb5 = 0, то:
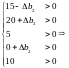
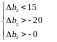
і інтервал зміни Δb2 наступний: 0 < Δb2 < 15, звідки 20 < b2 < 35.
Це означає, що якщо кількість ресурсів 2 типу буде змінено в знайдених межах, то, незважаючи на це, оптимальним планом двоїстої задачі залишиться Y = (40, 20, 40, 0, 0).
Згідно з цим, максимально можливий дохід підприємства перебуватиме в межах:
2200 +0 · 20 < zmax < 2200 +15 · 20
2200 < zmax < 2500
Якщо Δb1 = 0, Δb2 = 0, Δb4 = 0, Δb5 = 0, то:
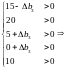
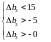
і інтервал зміни Δb3 наступний: 0 < Δb3 < 15, звідки 5 < b3 < 20.
Це означає, що якщо кількість ресурсів 3 типу буде змінено в знайдених межах, то, незважаючи на це, оптимальним планом двоїстої задачі залишиться Y = (40, 20, 40, 0, 0).
Згідно з цим, максимально можливий дохід підприємства перебуватиме в межах:
2200 +0 · 40 < zmax < 2200 +15 · 40
2200 < zmax < 2800
Якщо Δb1 = 0, Δb2 = 0, Δb3 = 0, Δb5 = 0, то:
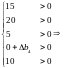
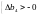
і інтервал зміни Δb4 наступний: 0 < Δb4 < ∞, звідки 15 < b4 < ∞.
Це означає, що якщо кількість ресурсів 4 типу буде змінено в знайдених межах, то, незважаючи на це, оптимальним планом двоїстої задачі залишиться Y = (40, 20, 40, 0, 0).
Згідно з цим, максимально можливий дохід підприємства перебуватиме в межах:
2200 +0 · 0 < zmax < 2200 +M · 0
2200 < zmax < 2200
Якщо Δb1 = 0, Δb2 = 0, Δb3 = 0, Δb4 = 0, то:
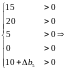
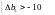
і інтервал зміни Δb5 наступний: –10 < Δb5 < ∞, звідки 0 < b5 < ∞.
Це означає, що якщо кількість ресурсів 5 типу буде змінено в знайдених межах, то, незважаючи на це, оптимальним планом двоїстої задачі залишиться Y = (40, 20, 40, 0, 0).
Згідно з цим, максимально можливий дохід підприємства перебуватиме в межах:
2200 –10 · 0 < zmax < 2200 +M · 0
2200 < zmax < 2200 → тобто кількість ресурсів 5 типу на розв’язок задачі не впливає.
Таким чином, якщо кількість одного з типів ресурсів належить відповідному інтервалу, а кількість інших ресурсів залишиться початковим, то план двоїстої задачі не зміниться.