1.2. Проста лінійна економетрична модель: побудова і аналіз

1.1. . Побудувати економетричну модель залежності урожайності зернових культур (у), ц/га від рівня внесення мінеральних добрив на 1 га (х), ц д. р. Розрахунки наводимо в таблиці 1.

Таблиця 1.1. Вихідні і розрахункові дані для побудови економетричної моделі

№	хі	уі	хі²	уі²	хіуі	yiхі2	уі -	(хі - )²	і	ui	ui²	(уі - )²
1	1,83	25,2	3,3489	635,04	46,116	84,392	0,392	0,029	23,746	1,454	2,114	0,154	1,128
2	2,44	19,7	5,9536	388,09	48,068	117,286	-5,108	0,193	27,528	-7,828	61,278	26,092	7,398
3	2,37	24,7	5,6169	610,09	58,539	138,737	-0,108	0,136	27,094	-2,394	5,731	0,012	5,226
4	1,06	18,6	1,1236	345,96	19,716	20,899	-6,208	0,886	18,972	-0,372	0,138	38,539	34,059
5	2,07	25,1	4,2849	630,01	51,957	107,551	0,292	0,005	25,234	-0,134	0,018	0,085	0,181
6	1,66	21,1	2,7556	445,21	35,026	58,143	-3,708	0,116	22,692	-1,592	2,534	13,749	4,477
7	2,39	28,3	5,7121	800,89	67,637	161,652	3,492	0,151	27,218	1,082	1,171	12,194	5,808
8	1,01	18,2	1,0201	331,24	18,382	18,566	-6,608	0,982	18,662	-0,462	0,213	43,666	37,773
9	2,47	32	6,1009	1024	79,04	195,229	7,192	0,220	27,714	4,286	18,370	51,725	8,445
10	1,6	30,1	2,56	906,01	48,16	77,056	5,292	0,161	22,320	7,780	60,528	28,005	6,190
...	...	...	...	...	...	…	...	...	...	...	...	...	...
23	1,75	23	3,0625	529	40,25	70,438	-1,808	0,063	23,250	-0,250	0,063	3,269	2,427
24	1,96	26,2	3,8416	686,44	51,352	100,650	1,392	0,002	24,552	1,648	2,716	1,938	0,066
25	2,45	30,9	6,0025	954,81	75,705	185,477	6,092	0,201	27,590	3,310	10,956	37,112	7,740
∑	50,03	620,2	105,8725	15906,6	1276,92	2763,373	0	5,751	620,186	0,014	242,3441	520,718	221,086

Виходячи з методу найменших квадратів, для знаходження невідомих параметрів â₀ , â₁ , запишемо систему нормальних рівнянь:

nâ₀ + â₁∑х_i =Σ y_i 25â₀ +50,03 â₁ = 620,2

â₀ ∑х_i + â₁∑х_i ²= Σ y_i x_i 50,03â₀ + 105,872â₁=1276,921

Поділимо кожне рівняння системи на коефіцієнти при параметрі â₀

â₀ +2,0012 â₁ = 24,808

â₀ +2,1162 â₁ = 25,5231

Віднімемо від другого рівняння перше і одержимо:

0,115 â₁ =0,7151. Звідси â₁=6,2. Підставимо це значення в перше рівняння останньої системи і знайдемо â₀ : â₀= 24,808 – 2,0012×6,2183=12,4. Отже економетрична модель має вид (для фактичних значень залежної змінної)

Y = 12,4 + 6,2 x + u.

Оскільки, вільний член моделі â₀ ≠ 0, то урожайність зернових культур не є строго пропорційною до рівня внесення мінеральних добрив, â₁ = 6,2 показує, що при додатковому внесенні на 1 га 1 ц д. р. мінеральних добрив урожайність збільшиться на 6,2 ц/га.

Еластичність урожайності щодо рівня внесення мінеральних добрив визначається коефіцієнтом еластичності :

Е = = = 0,5 %.

Значення цього коефіцієнта слід тлумачити так : при збільшенні внесення мінеральних добрив на 1% урожайність зернових культур зросте на 0,5%.

Залишки обчислюються згідно з рівністю :

u_i = y_i – ŷ_i..

Оцінка дисперсії залишків подається так :

= =10,5367, =3,246.

Для залишків u_i можна задати певну функцію закону розподілу, наприклад функцію нормального розподілу.

Оцінкою фактичного коефіцієнта кореляції є вибірковий коефіцієнт кореляції, який можна обчислити за формулою :

,

= , = 0,4797;

= , =4,5637 ;

= =0,6537.

Вибірковий коефіцієнт кореляції є точковою оцінкою фактичного коефіцієнта кореляції і тому потребує перевірки на суттєвість. Вона базується на критерії Стьюдента за формулою :

t= , r −вибірковий коефіцієнт кореляції, n-m− число ступенів вільності.

Якщо t › t_табл. , де t_табл. − відповідне табличне значення t розподілу з (n –m) ступенями вільності та рівнем значущості α, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежною змінними моделі. Для нашого прикладу :

t= = = =4,1424.

Табличне значення t − критерія для рівня значущості α =0,05 і n−m=23 ступенів свободи дорівнює 2,0687. Оскільки t › t_табл. робимо висновок, що коефіцієнт кореляції є значущим і зв’язок між x та y є суттєвим.

Для аналізу якості опису існуючої залежності між двома ознаками часто використовують індекс кореляції. Він розраховується за формулою :

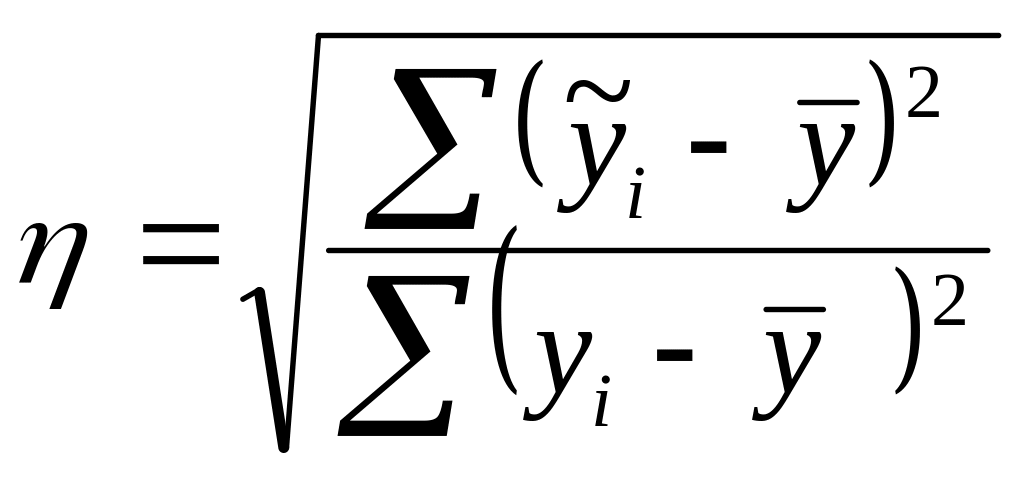= =0,6516≈0,65.

Перевірку гіпотези про значущість параметрів економетричної моделі можна виконати згідно з t- критерієм:

t_j= .

Обчислене значення t- критерію порівнюється з табличним для вибраного рівня істотності і n-m ступенів свободи. Якщо t_факт> t_табл, то відповідний параметр економетричної моделі є достовірним.

Дисперсії параметрів економетричної моделі можна визначити за формулами:

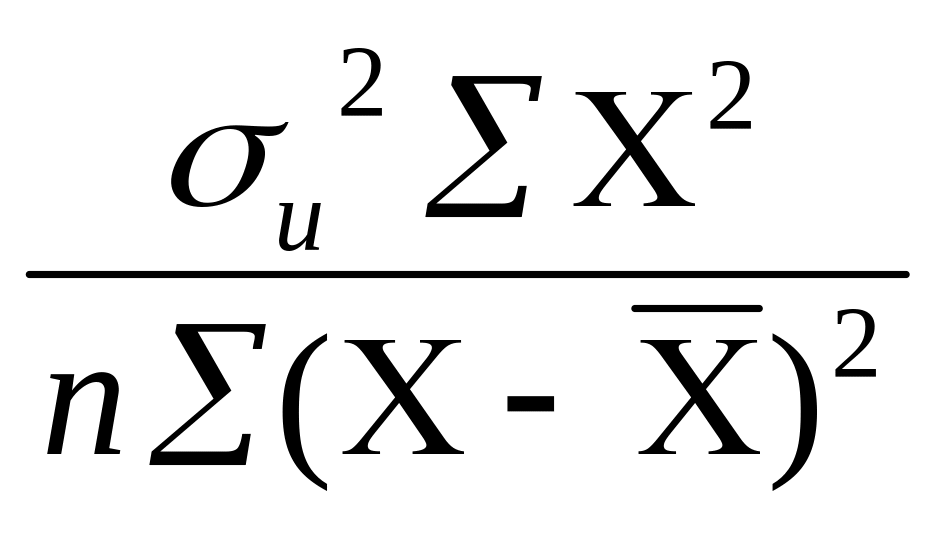= = =117,62, =10,85;

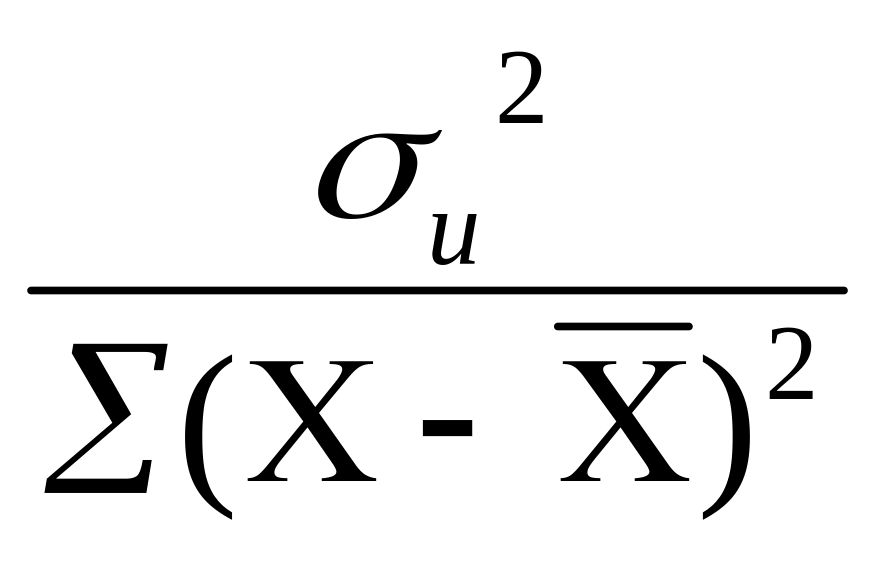= = ⁼0,00098, =0,031.

Отже, перевіримо гіпотези про значущість оцінок параметрів моделі, побудованої на основі вихідних даних, наведених у табл. 1

t₁= = =16,13;

t₀= = =0,35.

Нехай число ступенів свободи n-m =25-2=23 і рівень значущості α=0,05, тоді t_табл=2,0687. Оскільки t_1факт> t_табл , то параметр â₁є значущий, t_0факт < t_{табл ,} то параметр â₀ є незначущим.

Для подальшого аналізу побудованої економетричної моделі визначимо коефіцієнт детермінації. Він показує, на скільки відсотків варіація результативної ознаки y визначається варіацією чинника х :

D = r²×100% = 0,65²×100% =42,25%. Це означає, що варіація урожайності на 42,25 % пояснюється дією мінеральних добрив і на 57,75 % впливом інших неврахованих випадкових чинників.

Перевірити на значущість коефіцієнт детермінації можна за допомогою F-критерію:

F_k-1,n-k= : .

Фактичне значення F-критерію порівнюється з табличним при ступенях свободи k-1 і n-k і при вибраному рівні значущості. Якщо F_факт > F_табл, то гіпотеза про значущість коефіцієнт детермінації підтверджується , у противному разі – відхиляється. У нашому випадку :

F_k-1,n-k= : = F_2-1,25-2= : =16,827.

Табличне значення F-критерію при ступенях свободи 1 і 23 і при рівні значущості 0,05 (F_1,23(0,05)) дорівнює 4,28. Оскільки F_факт >F_табл , можна зробити висновок про значущість коефіцієнта детермінації.

Перевірити модель на адекватність можна також за допомогою також F-критерію :

F_k-1,n-k= .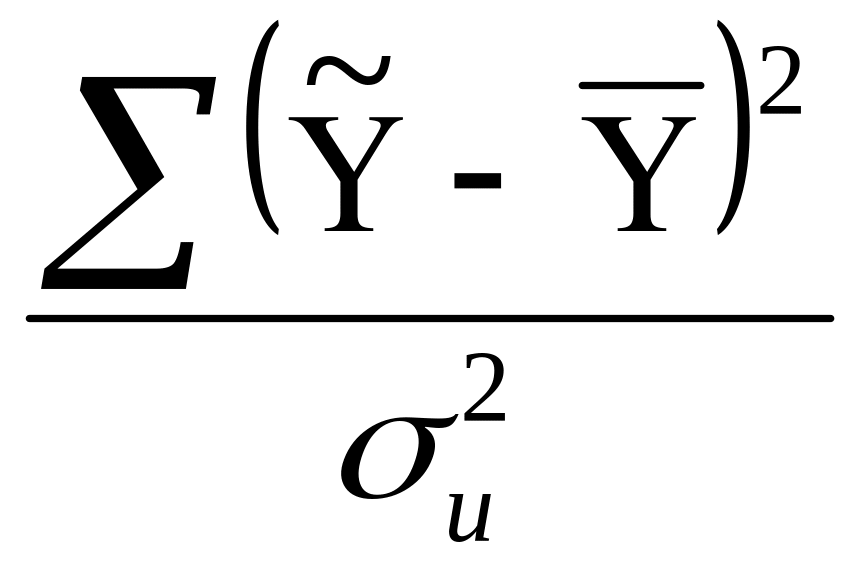

За даними табл. 1 фактичне значення критерія Фішера буде дорівнювати:

F_1,23= = = 20,982.

Оскільки F_факт >F_табл , можна зробити висновок, що побудована модель адекватна реальній дійсності.

Одним з важливих завдань економетричного моделювання є оцінка прогнозного значення результативної ознаки за умови, що значення чинника задано на перспективу. На основі побудованої економетричної моделі можна отримати точковий прогноз результативної ознаки на перспективу. Нехай x_прогн=3 ц д. р., тоді y_прогн=12,4 + 6,2 x_прогн= 12,4 + 6,2 3=31 ц/га.

На основі точкового прогнозу можна побудувати інтервальний прогноз скориставшись формулою:

y_прогн ± t_табл .

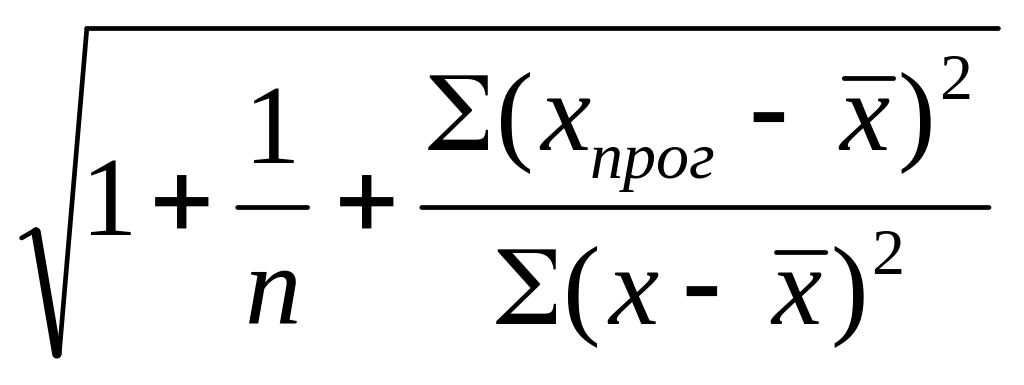Для нашої моделі за даними табл. 1 інтервальний прогноз для залежної змінної буде такий:

31 ± 2,0687 3,246 =31 ± 12,4692 1,1017=31±13,74 .

Отже з імовірністю 1-α = 0,95 можна стверджувати, що при рівні внесення мінеральних добрив в розмірі 3 ц д. р. врожайність зернових культур будеь коливатись в межах від 17,26 (31 - 13,74=17,26) до 44,74 ( 31 + 13,74=44,74) ц/га.