Условные обозначения
Пусть f(z) — многочлен Гурвица над комплексными числами. f не имеет комплексных коэффициентов и все корни f лежат в левой полуплоскости. Разложим f в положительную пару:
f(z) = g(z2) + zh(z).
Обозначим
коэффициенты g
как
,
а h
— как
.
Внимание! Они пронумерованы «с конца»,
то есть ведущим коэффициентом многочлена
g
является
.
Определим матрицу Гурвица как выстроенные «лесенкой» нечётные и чётные коэффициенты:
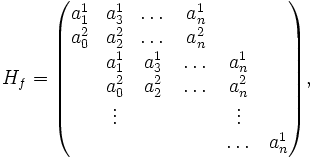
в зависимости от степени многочлена, в последней строке будут чётные или нечётные коэффициенты. Все главные миноры этой матрицы положительны, если f — многочлен Гурвица, и наоборот.
Критерий устойчивости Рауса
Цепочка
Штурма,
начинаюшаяся многочленами g
и h,
определяет последовательность
ведущих
коэффициентов многочленов цепочки. Все
элементы этой последовательности имеют
строго одинаковый знак, если f
— многочлен Гурвица, и наоборот.
Существует более общая версия критерия Рауса: количество корней в правой полуплоскости равно количеству перемен знака в цепочке.
Обратите также внимание, что в записи
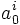число
i
— индекс, а не степень.
Критерии Гурвица и Рауса эквивалентны. Они оба характеризуют стабильные по Гурвицу многочлены.
Применив
метод
Гаусса
к матрице Hf
, мы получим диагональную матрицу
.
Однако теперь критерий Гурвица
соответствует требованию «все элементы
трансформированной
матрицы имеют одинаковый знак». Если
же подробно рассмотреть, как метод
Гаусса трансформирует матрицу Hf,
мы получим условия генерации цепочки
Штурма. Убедившись, что коэффициенты
соответствуют
коэффициентам
,
мы и получим критерий Рауса.
6.2. Примеры выполнения заданий контрольной работы
Задание 1.
Характеристическое уравнение замкнутой автоматической системы имеет вид 0,005p6 + 0,1p5 + 2,5p4 + 20p3 + 50p2 + 60p + 150 = 0.
C помощью критерия Рауса определить устойчивость данной системы.
Решение.
Критерий Рауса формулируется так:
Для того чтобы система была устойчивой, необходимо и достаточно, чтобы все величины (элементы) первого столбца таблицы Рауса были положительными при положительном коэффициенте ап характеристического уравнения (табл.6).
Таблица 6
Значения |
№ стр |
Номер столбца |
|||
I |
II |
III |
IV |
||
|
1 |
0,005 |
2,5 |
50 |
150 |
|
2 |
0,1 |
20 |
60 |
0 |
r0= |
3 |
c13=2,5-0,05*20=1,5 |
c23=50-,05*60=47 |
c33= 150 |
0 |
r1= |
4 |
c14=20-0,067*47=16,85 |
c24=60-0,067*150 =49,95 |
0 |
0 |
r2= |
5 |
c15=47-0,089*49,95= =42,55 |
c25= 150 |
0 |
0 |
r3= |
6 |
c16=49,95-0,4*150= =-10,05 |
0 |
0 |
0 |
r4= |
7 |
c17= 150 |
0 |
0 |
0 |
Ответ:
Так как не все величины первого столбца таблицы положительные (c16 = -10,05), то эта система будет неустойчивой.
Задание 2.
Характеристическое уравнение системы имеет вид
20p3 + 25p2 + 10p + 10 = 0.
C помощью критерия Гурвица определить устойчивость данной системы.
Решение.
Составим таблицу Гурвица.
25 |
10 |
0 |
20 |
10 |
0 |
0 |
25 |
10 |
Определитель
1
= 25 > 0.
Определитель
|
25 |
10 |
|
|
|
|
=25*10 - 20*10 = 50 > 0. |
|
20 |
10 |
|
Определитель
|
25 |
10 |
0 |
|
3 = |
20 |
10 |
0 |
= 25*10*10 - 20*10*10 = 500>0. |
|
0 |
25 |
10 |
|
Критерий Гурвица формулируется следующем образом:
Система
устойчива, если
и все определители Гурвица больше нуля,
т.е.
,
где
.
Ответ:
Так
как определители
>0,
то данная система устойчива.
Задание 3.
C помощью критерия Михайлова определить устойчивость системы, характеристическое уравнение которой имеет вид.
3*10-4p5 + 5*10-3p4 + 0,1p3 + 0,5p2 + 0,9p + 1 = 0
Решение.
Kритерий Михайлова можно сформулировать так:
Вектор кривой Михайлова D(jω) устойчивой системы при изменении w от 0 до 00 начинает своё движение на вещественной положительной (т.е. в порядке 1-2-3-4-1….) n квадрантов координатной плоскости. Функция D(jω) на комплексной плоскости изображается вектором, начало которого расположено в точке 0, а конец определяется координатами U(ω) и V(ω).
C увеличением w модуль (длина) и фаза вектора изменяются и конец его описывает кривую, называемую годографом Михайлова (кривой Михайлова).
D(p) = 3*10-4p5 + 5*10-3p4 + 0,1p3 + 0,5p2 + 0,9p + 1.
Заменив p= jω, получим функцию:
D(jω) = 3*10-4(jω) 5 + 5*10-3(jω) 4 + 0,1(jω) 3 + 0,5(jω) 2 + 0,9(jω) + 1.
Для построения кривой Михайлова определяем вещественную U(ω) и мнимую V(ω) части функции D(jω):
U(ω) = 1 - 0,5ω 2 + 5*10-3ω 4,
V(ω) = 0,9 - 0,1ω 3 + 3*10-4ω 5.
Вычислим U(ω) и V(ω) для ряда значений частоты ω. Результаты вычислений сведём в таблицу (табл.7) и отобразим на графике (Рис. 1):
Таблица 7
ω |
0 |
5 |
10 |
12 |
15 |
18 |
20 |
|
U |
1 |
-8,4 |
1 |
32,7 |
141,6 |
363,8 |
601 |
+ |
V |
0,9 |
-10,7 |
-69,1 |
-97,2 |
-108,8 |
-15,4 |
161,9 |
+ |
jV(w)
U(w)
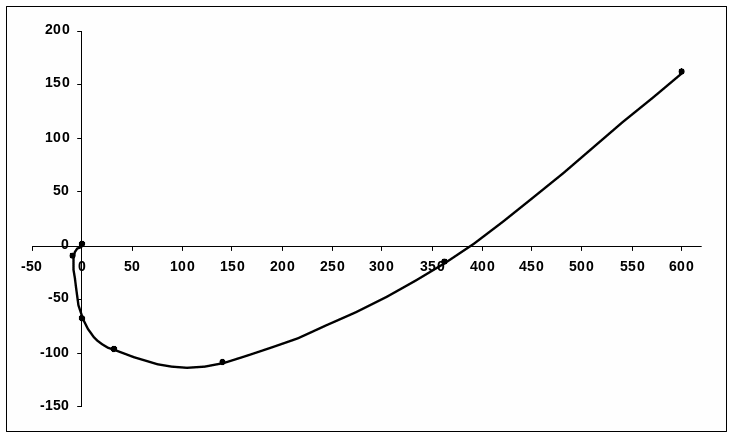
Рис. 1 Результат вычислений U(ω) и V(ω) для ряда значений частоты ω
Ответ:
Система устойчива, так как кривая Михайлова последовательно проходит через три квадранта в положительном направлении.