
- •Теория информационных процессов и систем
- •230201 - «Информационные системы и технологии» направления 654700 – «Информационные системы»
- •Научный редактор ю.М.Казаков
- •Введение
- •Дидактические единицы
- •Объем дисциплины и учебной нагрузки
- •Рабочая программа дисциплины содержание дисциплины
- •Тематический план лекций (18 часов)
- •Пояснения к изучению дисциплины
- •Перечень лабораторных работ (4 часа)
- •Задания на контрольные работы
- •6. Методические указания к решению и оформлению контрольной работы
- •6.1. Общие сведения
- •Условные обозначения
- •Критерий устойчивости Рауса
- •6.2. Примеры выполнения заданий контрольной работы
- •7. Вопросы к экзамену по дисциплине
- •8. Список рекомендуемой литературы Основная
- •Дополнительная
- •Научный редактор ю.М.Казаков
- •Темплан 2010 г., п.254
6. Методические указания к решению и оформлению контрольной работы
6.1. Общие сведения
Один из методов анализа линейной стационарной динамической системы на устойчивость- это критерий устойчивости Рауса. Наряду с критерием Гурвица, критерий Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких как критерий устойчивости Найквиста-Михайлова. К достоинствам метода относятся простая реализация на ЭВМ, а также простота анализа для систем небольшого (до 3) порядка. К недостаткам можно отнести ненаглядность метода, по нему сложно судить о степени устойчивости, о её запасах.
Метод
работает с коэффициентами
характеристического уравнения системы.
Пусть
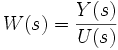 —
передаточная
функция
системы, а
—
передаточная
функция
системы, а
![]() —
характеристическое уравнение системы.
Представим характеристический полином
—
характеристическое уравнение системы.
Представим характеристический полином
![]() в
виде
в
виде
![]() .
.
Критерий Рауса представляет собой алгоритм, по которому составляется специальная таблица, где записываются коэффициенты характеристического полинома:
в первой строке записываются коэффициенты уравнения с чётными индексами в порядке их возрастания;
во второй строке — с нечётными;
остальные элементы таблицы определяется по формуле:
 ,
где
,
где
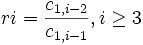 —
номер строки,
—
номер строки,
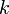 —
номер столбца;
—
номер столбца;
число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Таблица 5
Таблица Рауса
|
|
1 |
2 |
3 |
4 |
- |
1 |
|
|
|
.. |
- |
2 |
|
|
|
.. |
|
3 |
|
|
|
... |
|
4 |
|
|
|
... |
... |
.. |
... |
... |
... |
.. |
Формулировка критерия Рауса:
Для
устойчивости линейной
стационарной системы необходимо и
достаточно, чтобы коэффициенты первого
столбца таблицы Рауса
![]() были
положительными. Если это не выполняется,
то система неустойчива.
были
положительными. Если это не выполняется,
то система неустойчива.
Критерий устойчивости Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость. Наряду с критерием Рауса, критерий Гурвица является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких как критерий устойчивости Найквиста. К достоинствам метода относятся простая реализация на ЭВМ, а к недостаткам — малая наглядность.
Метод работает с коэффициентами характеристического уравнения системы. Пусть — передаточная функция системы, а — характеристическое уравнение системы. Представим характеристический полином в виде
.
Из
коэффициентов характеристического
уравнения строится определитель Гурвица
![]() по
алгоритму:
по
алгоритму:
1)
по главной диагонали слева направо
выставляются все коэффициенты
характеристического уравнения от
![]() до
до
![]() ;
;
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3)
на место коэффициентов с индексами
меньше нуля или больше
![]() ставятся
нули.
ставятся
нули.
Тогда согласно критерию Гурвица:
Для того чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.
