Маркетинг

Ситуация 1. Проанализируйте потребности человека в еде, апельсиновом со­ке, часах, детских игрушках, женских украшениях, общественном транс­порте, кабельном телевидении, подписке на газету «Ком­со­мольская прав­да» и др. При этом на основе матрицы потребностей необходимо по­­нять структуру потребности, т.е.

– понять причины возникновения потребности, её сущест­во­ва­ния, из­менения и удовлетворения;

– разобраться в иерархии ее признаков, проследить их связь;

– определить ее место и перспективы в рыночном окружении, а также коммерческие возможности её разработки.

Потребность в еде – постоянная потребность, возникает при рождение, в пирамиде маслоу находится в основании.

Потребность в апельсиновом соке не постоянная, усиливается в жару, при увеличение достатка человека увеличивается потребность.

Потребность в детских игрушках - возникает при появление детей,

Ситуация 2. Позиционирование новой торговой марки: Повседневный «Спортмастер». Вопросы и задания:

1. Проведите сегментацию рынка продукции компании «Спорт­мастер» по признакам сегментации.

Сегмент: активные люди, занимающиеся спортом

2. Выделенные целевые сегменты охарактеризуйте и сравните по критериям сегментации.

3. Какое позиционирование использует компания «Спорт­мас­тер»? Выскажите Ваше мнение по этому поводу.

4. Оцените возможность нового casual-брэнда по завоеванию до­ли на рынке.

5. Разработайте свои предложения к комплексу маркетинга фирмы для выбранного целевого рынка.

Ситуация 3. Предприятие «Норд» осваивает новые рын­­ки. Вопросы

1. Изучить информацию о товаре, целевом рынке и конку­ри­рую­щих това­рах.

2. Выявить конкурирующий товар, который следует выбрать в качестве базового.

3. Оценить показатели конкурентоспособности 3-х марок холо­диль­ников предприятия «Норд».

4. Основываясь на результатах анализа, из 3-х марок холо­диль­ников выбрать одну, которая в наибольшей степени соответствует условиям целевого рынка.

Ситуация 4. Создание телевизионного рекламного ролика. Задание:

1. Разработайте критерии оценки сценария рек­лам­ного ролика (товар по выбору).

2. Составьте варианты рекламных роликов для выбранных объек­тов.

3. После завершения работы представьте свою разработку сце­на­рия для оценки по разработанным критериям.

Макроэкономика

Задача 1. Страна с открытой экономикой характеризуется следующими дан­ными: ВНП = 1000 ден.ед.; потребит. расходы = 700 ден.ед., гос. закупки = 150 ден. ед.; функция инвестиций – I = 250 – 10r; ставка процента r = 5 %. Определите объем чистого экспорта страны.

AD = C+I_g+гос. расходы + X_n

X_n= 1000-150-20-700= 130

Задача 2. Известно, что объем потенциального ВНП, характеризующийся 6%-ным уровнем безработицы, составляет 5000 млрд. долл. В текущем году объем реального ВНП составил 4500 млрд. долл. В будущем году предполагается экономический подъем с соответствующим ростом объема реального ВНП до 4750 млрд. долл. Определите, как изменится уровень безработицы в стране в соответствии с законом Оукена (коэффициент Оукена – 2,5).

5000-4500 / 5000 *100% = 10%

10% / 2,5 = 4

4%+6%=10%

5000-4750 / 5000 *100% = 5%

5% / 2,5 = 2

2%+6%=8%

10-8 = 2%

Задача 3. Экономика страны характеризуется следующими данными: Факти­ческий доход (Y) = 4000 долл. Предельная склонность к потреблению MPC = 0,8. Равновесный доход (Y^*) = 4200 долл. Как должны изменится правительственные расходы (при прочих равных условиях) для того, чтобы экономика достигла равновесного состояния?

M_I(k) = 1/(1-MPC)= 1/(1-0,8)=5

M_k= Y/C; 4200-4000/С=5 С= 40

Задача 4. Экономисты страны А полагают, что зависимости потребительских расходов (С) и инвестиций (I) от величины ВНП (Y) выражаются в следующих уравнениях (млрд. долл.):

C = 8+0,6Y;

I = 0,1Y.

По их оценкам, правительственные расходы на покупку товаров и услуг в следующем году должны составить 50 млрд. дол., а чистый экспорт – 5 млрд. долл. Рассчитайте прогнозируемый на следующий год уровень ВНП.

ВНП= С+I+G+X_n

Y=8+0,6 Y+0,1Y+50+5

0,3Y=63

Y=210

Ответ 210 млрд$

Задача 5. Валовой национальный продукт в условиях полной занятости со­став­ляет 20 млрд. долл. Фактический объем ВНП равен 16 млрд. долл. Сумма налогов составляет 10 % от величины ВНП. Государственные расходы на товары и услуги равны 1,8 млрд. долл.

а) Определите, сводится ли государственный бюджет с дефицитом или излишком и установите его размеры.

б) Определите, как изменится сальдо государственного бюджета в условиях достижения полной занятости.

Решение:

А. Налоговые поступления составляют 16млрд. долл. * 10% = 1,6 млрд. долл. Дефицит бюджета составляет 1,8 – 1,6 = 0,2 млрд. долл.

Б. При полной занятости налоговые поступления от ВНП составили бы 20 млрд. долл * 10% = 2 млрд. долл. Тогда госбюджет имел бы профицит в размере 2 – 1,8 = 0,2 млрд. долл.

Микроэкономика

Задача 1. Спрос на землю описывается уравнением Q=100-2R, где Q – площадь используемой земли, R – ставка ренты (в тыс. руб. за га). Какова будет равновесная ставка ренты, если площадь доступных угодий составляет 90 га? Какова будет цена 1 га земли, если ставка банковского процента составит 12%.

Равновесный уровень 100-2R=90 R=5т.р.

Цена земли = рента/ставка банковского % = 5/0,12= 41,6 т.р.

Задача 2. К концу года бухгалтер говорит вам, что ваша прибыль 50000 долл. Управляя своей собственной фирмой, Вы упускаете зарплату в 30000 долл., которую Вы могли бы получить, работая в другом месте. 10000 личных средств Вы вложили в свой бизнес. Предполагая, что Вы упускаете 15 % с этих фондов подсчитайте экономическую прибыль. Останетесь ли Вы в этом бизнесе на следующий год?

1. Прибыль = выручка – издержки

2. Бух. Прибыль = выручка – внешние(явные) издержки

3. Экон. Прибыль = выручка – внешние(явные) издержки – внутр.издержки

Бух. Прибыль =50000 долл

Экон. Прибыль =50000долл-30000долл-10000*0,15 = 1850долл

В бизнесе следует остаться так как прибыль положительная

Задача 3. Предприятие находится в условиях совершенной конкуренции. Функция общих затрат от выпуска продукции представлена в таблице:

Выпуск продукции в единицу времени (Q), шт.	Общие затраты (ТС), ден. ед.
0	16
1	24
2	34
3	46
4	60
5	76

Если цена товара 9 ден. ед., какой объем производства следует выбрать? Ниже какого уровня должна снизиться цена, чтобы прекратилось производство? Проанализируйте полученный результат.

Выпуск продукции в единицу времени (Q), шт.	Общие затраты (ТС), ден. Ед.	Пределные издержки (MC).	Валовая выручка (TR).	Прибыль (TR-TC)	Перменные издержки (VС)	Средние переменные издержки (AVC)	Постоянные издержки (FС)	Предельная выручка (MR)
0	16	---	0	-16	0	---	16	9
1	24	8	9	-15	8	8 min	16	9
2	34	10	18	-16	18	9	16	9
3	46	12	27	-19	30	10	16	9
4	60	14	36	-24	44	11	16	9
5	76	16	45	-31	60	12	16	9

Если цена товара 9 ден. ед., какой объем производства следует выбрать? Ниже какого уровня должна снизиться цена, чтобы прекратилось производство? Проанализируйте полученный результат.

MC 8=24-16, 10=34-24, 12=46-34 и т.д.

TR из условия = 9 и по возрастающей 9+9=18, 18+9=27 и т.д.

FC = TC при 0 выпуске продукции

TC=FC+VC => VC=TC-FC

В условиях совершенной конкуренции MR=Pe=9 ден.ед. (из условия)

Фирма прекратит производство при цене ниже 8 ден.ед., т.е. AVC-min

Задача 4. Рыночный спрос на труд описывается формулой L = 70-W (L – объем использования труда, тыс. чел. – час; W – ставка заработной платы, долл. за час). Рыночное предложение труда описывается формулой L = 4W – 30. Государство устанавливает уровень минимальной заработной платы 30 долл. за час. Определите влияние этой меры на состояние рынка труда (вызовет ли она безработицу, и если да, то какого масштаба).

L_D=L_S

70-W_E = 4 W_E - 30

5 W_E = 100

W_E = 20$

L_D(30)=70-30=40

L_S(30)=120-30=90

Объем безработицы = L_S -L_D=90-40=50 тыс. чел/час

W_min≥ W_E? следов. Безработица

Задача 5. По данным таблицы рассчитайте средние валовые, средние постоянные, средние переменные и предельные издержки, изобразите данные величины графически и проанализируйте их динамику в зависимости от объемов выпуска.

Выпуск, шт.	Общие издержки ден.ед. (TC)
0	40
1	120
2	160
3	220
4	300
5	400
6	520
7	660
8	820

Выпуск, шт.	Общие издержки ден.ед. (TC)	Средние общие издержки АТС	Сред. премен. издерж АVC	Сред. пост. издерж АFC	MC
0	40	--	-	-	-
1	120	120	0	40/1=40	120-40/1-0 = 80
2	160	80	60	40/2=20	40
3	220	73	60	13,3	60
4	300	75	65	10	80
5	400	80	72	8	100
6	520	87	80	6,6	120
7	660	91	88	6	140
8	820	103	98	5	160

FC	VC	MC	ATC	AVC	AFC
40	-	-	--	-	40
40	80	80	120	0	20
40	120	40	80	60	13,3
40	180	60	73	60	10
40	260	80	75	65	8
40	360	100	80	72	6,6
40	480	120	87	80	6
40	620	140	91	88	5
40	780	160	103	98

АТС = TC/Q

АFC = FC/Q

АVC = VC/Q = АТС – АFC

VC = TC – FC

MC = ∆ TC/∆Q Графики по этим данным, по оси Х – ATC, AVC, AFC, MC; по оси У - Q

Менеджмент

Задача 1. Два экскаватора, имеющие разную производительность способны вырыть котлован за 8 часов фактически сначала 4 часа работал первый экскаватор, затем 8 часов – второй. Они выполнили лишь 60% работы по рытью котлована. За сколько часов каждый экскаватор может вырыть котлован самостоятельно? 10 и 40 часов.

8(x+y) – 100%

4x+8y – 60%

8(x+y)*60/10=(4x+8y)*100/10

48х+48у=40x+80y

8x=32y

x=4y

8(x+y)=100

8(4y+y)=100

40y=100

Y=2,5

X=10

100/2,5=40 часов y экскаватор

100/10=10 часов х экскаватор

Задача 2. На строительство типового здания строительное предприятие №1 тратит 3 года, предприятие №2 – 2 года, предприятие №3 – 4 года а предприятие №4 – 1 год. За какое время построят дом четыре предприятия совместно?

№1 1 здание – 3 года; 1 – 1/3=0,33

№2 1 здание – 2 года; 1 год – 1/5=0,5

№3 1 здание – 4 года; 1 год – 1/4=0,25

№4 1 здание – 1 года; 1 год – 1/1=1

За 1 год они вместе строят 0,33+0,5+0,24+1=2,07

Следовательно 1 здание они построят за 1/2,07=0,48

Находим, какие доли дома строительные организации строят за один год, и суммируем эти доли: 7, + 72 + 74 + 1 = 25/12 дома.

Исходя из того, что эта суммарная доля строится за 365 дней, рассчитываем (из пропорции), за сколько дней строится единица дома:

365*12/25 = 175 дней

Задача 3. На собрании трудового коллектива число отсутствующих равнялось 20% от числа присутствующих. Уход с собрания еще 10 человек привел к тому, что процент отсутствующих вырос до 30. Сколько всего членов в трудовом коллективе?

Принимая число присутствующих на собрании за х, мож­но написать:

0,2х+ 10 = 0,3(х- 10), откуда х = 130 человек.

Всего в коллективе 130 = 0,2 • 130 = 156 человек.

Задача 4. Двое партнеров по товариществу Семенов и Федоров, договорились иметь общий счет в банке, с которого будут снимать в течение каждого месяца по определенной постоянной сумме. Рассчитано, что если счетом станет пользоваться только Семенов, т он исчерпает его за год, а если и Семенов, и Федоров вместе – за 8 месяцев. За сколько времени израсходовал бы деньги один Федоров?

Если бы у партнеров было 8 общих счетов, Семенов израсходовал бы их за 12 мес. • 8 = 96 мес. А Семенов и Федоров за 96 месяцев израсходовали бы 2 счетов.

Теперь понятно, что за эти же 96 месяцев Федоров израсхо­довал бы 12 счетов - 8 счетов = 4 счета.

Отсюда понятно, что один счет Федоров способен израсходовать за 96/4=24 месяца.

12х=8(х+у)

12х=8х+8у

X=2y, если сумма, которую снимает Федоров в два раза меньше, чем сумма Семенова, то Федоров израсходует деньги за 2 года.

Задача 5. Три работника внесли рационализаторские предложения по экономике ресурсов: первое – экономит 35% ресурсов, второе – 50%, третье – 15%. Сколько процентов ресурсов экономят все три предложения вместе?

Предположим, рассматривается экономия энергетичес¬ких ресурсов, эквивалентных 100 т топлива. Тогда в результате реализации первого предложения можно будет обойтись 65 т топ¬лива (100 - 35), после реализации второго предложения - 32,5 т (65 - 50 % от 65), после реализации третьего - 27,7 т (32,5 - 15 % от 32).

Таким образом, общая экономия составит: 100-27,7 = 72,3%.

Задача 6. Решение принимаются группой из двух лиц. Возможны два альтернативных варианта решения: а1 и а2. Оценки полезности этих вариантов даны в таблицах. Оценить матрицу средней полезности для группы.

Матрица полезности для 1-го лица.						Матрица полезности для 2-го лица.
Варианты решения	Вероятности исходов				Варианты решения		Варианты решения
	0,4	0,8					0,2	0,6
а1	- 8	+ 12				а1		- 2	+ 4
а2	+ 20	- 3				а2		+ 40	- 7

Поскольку 1-е лицо оценивает выше полезность перво­го варианта, а 2-е лицо - второго, при принятии группового реше­ния прийти к общему мнению невозможно. В этом случае теория решений обычно предлагает основываться на средних величинах: средних вероятностях исходов и средних полезностях (табл. Р.5.2). Теперь видно, что группа должна избрать вариант а₂.

Варианты решения	Средние вероятности исходов		Полезность по двум исходам
	0,3	0,7
а» а2	-5 +30	+8 -5	-5-0,3 + 8 0,7 = +4,1 +30-0,3-5-0,7 = +5,5

Задача 7. Ваш автомобиль снабжен двумя противоугонными приспособлениями: механическим и электрическим. Механическое приспособление имеет вероятность срабатывания 0,9 (из 10 раз оно срабатывает 9), а у электрического вероятность срабатывания = 0,8. Какова вероятность того, что Ваш автомобиль не угонят?

Решение

Расчет вероятности угона автомобиля. Р1 = 0,1 и Р2 = 0,2. По условию не очевидно, что данные устройства зависимы. По определению независимости 0.1*0.2 = 0,02

Вероятность не угона = 1- 0,02 = 0,98.

Задача 8. Вы располагаете 100 млн. рублей, которая решаете потратить на лотерею. Количество выпущенных лотерейных билетов – 10 млн. шт. Стоимость одного лотерейного билета 1 тыс. рублей. Величина выигрыша на «счастливый» билет -1 млн. рублей. Какова будет вероятность выигрыша при покупке 1 билета лотереи с учетом того, что Вы рассчитываете на прибыль от вложения равную 30%? 0,1

Всего – 100 000000

Кол-во билетов – 10 000 000

Стоимость 1 билета 1000

Величина выигрыша 1 000 000

Вероятность прибыль от вложения – 30%

Максимум мы можем купить 100 000 билетов

Мы рассчитываем, на прибыль в 30%, то есть на прибыль в 130 000 000. руб.

Если мы рассчитываем на такую прибыль, то в наших 100 000 билетов должно оказаться 130 000 000 / 1000 000  - 130 билетов выигрышных

Какова же вероятность, что в купленных нами 100 000 билетов 130 будут выигрышными?

P=0,0013*0,01=

130/100 000=0,0013

100000/10 000 000=0,1

Задача 9. При найме менеджера на работу в контракте было указано, что за год ему будет оплачиваться зарплата в размере 500 тыс. д.ед. и премия в виде телевизора или другой вещи подобной стоимости, которая выдается авансом в начале года. Менеджер разорвал контракт, проработав 7 месяцев. При увольнении он получил часть стоимости подарка 240 т.е.ед. В какую сумму была оценена выданная в начале года премия.

Средняя месячная оплата труда менеджера составляет:

260 тыс. у.д.ед./ 5 мес. = 52 тыс. у.д.ед. в месяц.

За 7 месяцев зарплата в деньгах составит:

52 тыс. у.д.ед. • 7 = 364 тыс. у.д.ед. Но за это время менеджер уже получил 240 тыс. у.д.ед. Следовательно, премия оценена в 364 - 240 = 124 тыс. у.д.ед.

Задача 10. На ферме в качестве корма для животных используются два продукта М и Н. Сбалансированное питание предполагает, что в день одно животное должно получать не менее 200 калорий, но особое внимание надо обратить на то, что бы потребление при этом количество жира не должно превышать 14 единиц. Рассчитано, что в одном кг. каждого продукта содержится:

В продукте М – 100 калорий и 4 единицы жира;

В продукте Н - 200 калорий и 4 единицы жира;

Как разработать максимально дешевый рацион откорма животных, отвечающий условиям дешевизны и сбалансированности питания, если:

Стоимость 1 кг. продукта М – 1,5 д.ед.;

Стоимость 1 кг. продукта Н – 2,5 д.ед.

Обозначая через х, и х₂ дневные нормы продуктов М и Н соответственно, можно по условию задачи составить следую­щие неравенства:

Условие жирности: 14jc, + 4х₂ < 4. (1)

Условие калорийности: 150х, + 200х₂ > 200. (2)

При этом очевидно, что х_{ >0,х₂> 0.

Требование минимизации расходов может быть записано так: \,5х_] + 2,5jc₂ - как можно меньше. (3)

Соотношения (1), (2) и (3) могут быть наглядно показаны на графике (рис. Р. 12).

Оптимальное решение о рационе соответствует точке В на графике, полученной при совместном решении неравенств (1) и (2). Этой точке соответствует:

дневное количество продукта М, равное 0,9 кг,

и дневное количество продукта Н, равное 0,32 кг.

С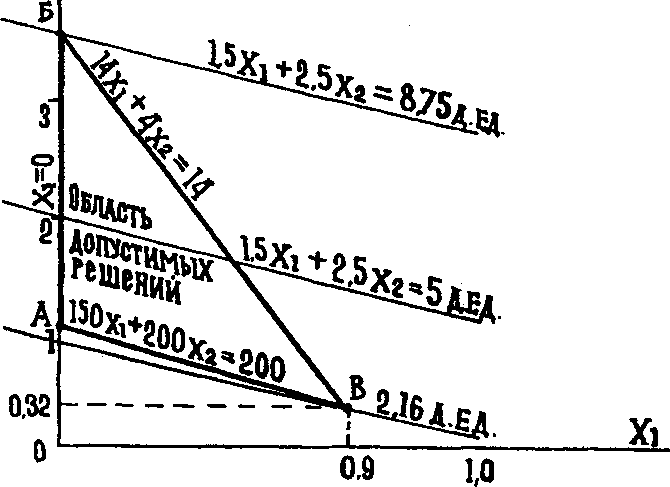 тоимость дневного рациона будет при этом минимальной и составит 2,16 у.д.ед.