Задача 2.2

Руководство птицефабрики имеет возможность закупать корма трех видов. Из этих кормов птицы должны получать питательные вещества (П1, П2, П3 и П4), требуемое количество которых и содержание в кормах (в ед.) приведены в таблице:

Питательные вещества	Корма			Нормы потребления
	К1	К2	К3
П1	3	5	0	равно 16
П2	2	2	4	не менее 24
П3	8	1	2	не менее 25
П4	4	3	5	не менее 33, но не более 40

Цены за 1 т кормов составляют соответственно 1000, 900 и 800 рублей.

Какие корма и в каком количестве следует закупать, чтобы затраты птицефабрики оказались минимальными?

Задача 2.3

Пищевой комбинат производит фруктовые джемы из персиков, абрикосов и апельсинов.

Дневной запас фруктов составляет 100 кг персиков, 80 кг абрикосов и 60 кг апельсинов. Кроме фруктов в джем входит сахар, запас которого считается неограниченным.

Цены на фрукты и их содержание в джемах указаны в таблице:

Джем	Содержание фруктов (в %)
	персики	абрикосы	апельсины
Д1	20	30	0
Д2	30	10	20
Д3	10	40	10
Цена за 1 кг (руб.)	40	30	30

Килограмм сахара стоит 15 рублей. Затраты на изготовление килограмма каждого джема составляют 20 рублей.

Готовый джем Д1 завод продает по 50 рублей за 1 кг, Д2 и Д3 - по 60 рублей за 1 кг.

Какова максимальная дневная чистая прибыль комбината?

Задача 2.4

Предприятие производит хлопья для завтрака "Три злака" №1, №2 и №3, в состав которых входят овсяные, пшеничные и кукурузные хлопья. Всего в распоряжение предприятия в неделю поступает 450 кг овсяных, 300 пшеничных и 800 кг кукурузных хлопьев по цене 20, 25 и 22 рубля за 1 кг соответственно.

Рецептура хлопьев "Три злака" требует соблюдения при смешивании следующих пропорций:

	Требуемые пропорции	Продажная цена (руб. за 1 кг)
"Три злака" №1	не менее 50% кукурузных, не более 30% овсяных	40
"Три злака" №2	не менее 60% кукурузных	60
"Три злака" №3	не более 40% пшеничных, не более 20% овсяных	50

Какова максимальная чистая прибыль предприятия в неделю?

Оптимальный раскрой

Общая постановка задачи: выбрать один или несколько способов раскроя и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов.

Такая задача решается в два этапа. На первом этапе определяются рациональные способы раскроя материала, на втором этапе формулируется и решается задача линейного программирования.

Рациональным (парето-оптимальным) называют такой способ раскроя, при котором увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида. Именно с нахождения всего множества рациональных способов раскроя начинают решение любой задачи этого типа.

На втором этапе, в зависимости от вопросов, поставленных в условии задачи, обычно применяют одну из трех основных моделей линейного программирования:

Модель с минимизацией расхода материалов:

(9)

Модель с минимизацией отходов:

(10)

Модель с максимизацией комплектов:

(11)

где: i - индекс способа раскроя;

k - индекс вида заготовки;

a_ik - количество заготовок вида k, полученных при раскрое единицы материала i-м способом;

b_k - число заготовок вида k в комплекте;

d - количество материала;

x_i - количество единиц материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя);

c_i - величина отхода, полученного при раскрое единицы материала по i-му способу;

y - число комплектов заготовок.

Пример решения задачи:

При изготовлении парников используются металлические стержни. Материал для их изготовления поставляется в виде исходных стержней длинной 220 см. Из них необходимо получить 80 стержней длиной 120 см, 120 стержней длиной 100 см и 102 стержня длиной 70 см.

Какое минимальное количество материала следует разрезать?

Решение:

Найдем все рациональные способы раскроя исходного материала на стержни длиной 120, 100 и 70 см. Таких способов пять:

Способы раскроя	120 см	100 см	70 см	Отходы, см
1	1	1	0	0
2	1	0	1	30
3	0	2	0	20
4	0	1	1	50
5	0	0	3	10

Обозначим за x₁ количество исходных стержней, разрезаемых по способу 1, за x₂ - количество исходных стержней, разрезаемых по способу 2 и т.д.

Используя модель линейного программирования с минимизацией расхода материала, получим:

(12)

Подготовим таблицу в Microsoft Excel, содержащую исходные данные задачи, введем формулы для расчета целевой функции и левой части ограничений, заполним форму модуля Поиск решения:

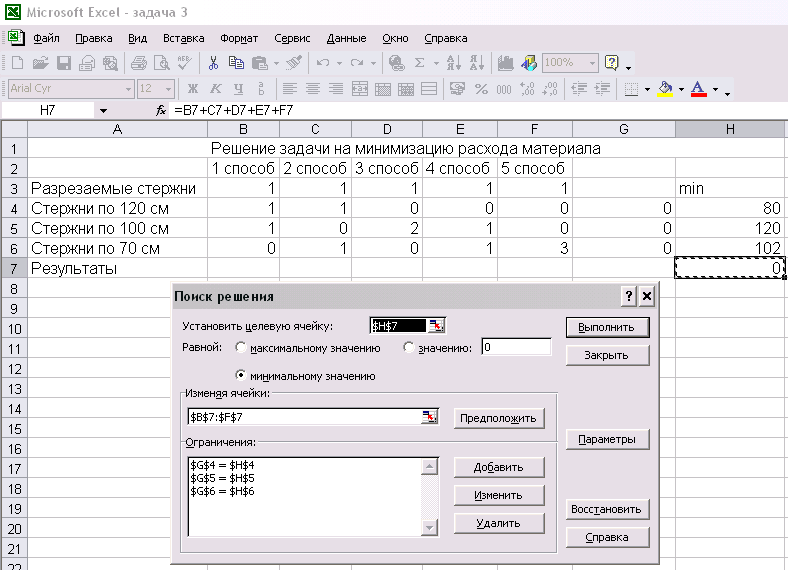
Рис. 17

С помощью модуля Поиск решения найдем, что для получения необходимого количества различных стержней нужно разрезать 134 исходных стержня, причем 80 исходных стержней нужно разрезать по 1-му способу, 20-по третьему и 34 по пятому способу:

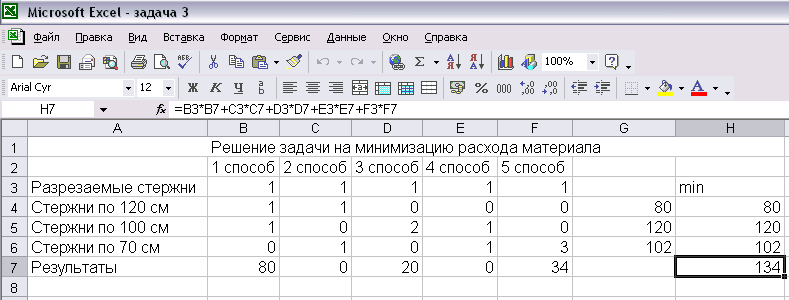
Рис. 18

Те же результаты можно получить, используя для расчетов систему Mathcad. В этом случае решение будет записано как показано на рис. 19.

Необходимо обратить внимание, что ограничения-равенства, встречающиеся в данном примере, содержат знак =, вводящийся с панели операторов отношений. Этот знак нельзя путать со знаками = (вывод результатов вычисления) и := (оператор присваивания).

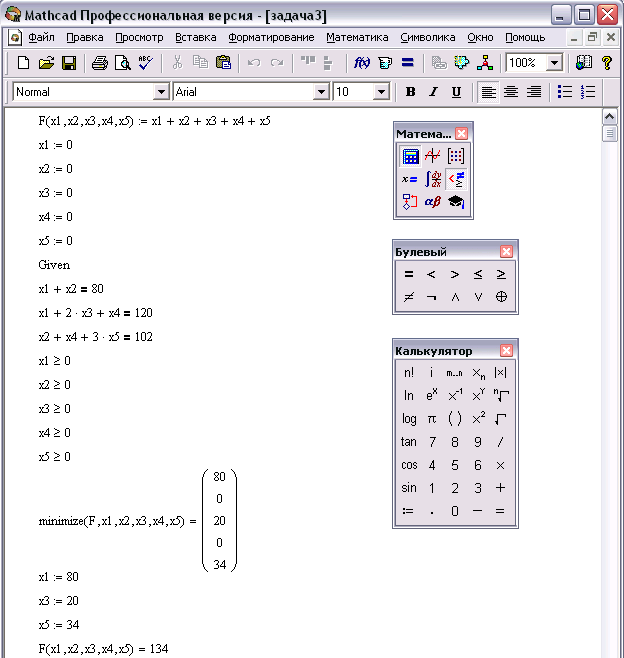
Рис. 19

Задачи

Задача 3.1

Один из цехов фабрики по пошиву изделий из кожи раскраивает поступающие заготовки для получения 5 видов деталей одним из трех возможных способов. Из одной заготовки получают:

Способ раскроя	Детали
	A	B	C	D	E
I	10	5	3	7	2
II	6	8	4	5	2
III	4	7	5	3	4

Требуется получить не менее 48 деталей вида А, не менее 32 деталей вида В, не менее 45 деталей вида С, не менее 17 деталей вида D и не менее 24 деталей вида Е.

Какое минимальное количество заготовок нужно раскроить?