Международный институт "ИНФО-Рутения"

89062951151

Н.А. Филина

Математические методы исследования в экономике

Методическое пособие

для студентов заочной (дистанционной) формы обучения

Под ред. д.т.н., проф. Н.Т. Катанаева

Москва 2006

Ф 53

Филина Н.А. Математические методы исследования в экономике: Методическое пособие. Под ред. д.т.н., проф. Н.Т. Катанаева. – М.: МИИР, 48 с., 2006.

В сборник методических пособий включен материал по основным разделам курса "Математические методы исследования в экономике" - оптимизации плана производства, оптимальному смешению, оптимальному раскрою, оптимальному финансированию, транспортным задачам и задачам о назначении.

По каждой теме даются теоретический материал и примеры решения задач при помощи программы Microsoft Excel пакета Microsoft Office и математической системы Mathcad.

Автором подробно изложены и показаны на примерах принципы решения оптимизационных задач в Microsoft Excel и Mathcad.

Рекомендуется для студентов экономических специальностей.

Подготовлено и издается по заказу Международного института "ИНФО-Рутения"

Печатается в авторской редакции.

Подписано в печать 11.05.2006. Сдано в производство 11.05.2006.

Формат бумаги 6090/16 Бум. множ. Гарнитура Times.

Усл.печ.л. 3,25 Уч.изд.л. 3,0 Тем. план 2006 г.

Тираж 500 Заказ № 1980

Ооп миир, 109280, Москва, ул. Автозаводская, д. 16.

© Филина Н.А., 2006.

© МИИР, 2006.

Содержание

Оптимизация плана производства 4

Оптимальное смешение 18

Оптимальный раскрой 25

Оптимальное планирование финансов 30

Транспортная задача 37

Задача о назначениях 45

Литература 51

Оптимизация плана производства

Общая постановка задачи:

Необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия - максимума прибыли, минимума затрат и т.д.

Модель:

(1)

(2)

(3)

где: n - количество выпускаемых видов продукции;

m - количество используемых видов ресурсов;

a_ij - объем затрат i-го ресурса на выпуск единицы j-й продукции;

b_i - имеющееся количество i-го ресурса;

c_j - прибыль от реализации единицы j-й продукции;

x_j - объем выпуска j-го вида продукции.

Выражение (1) является целевой функцией и отражает максимизацию прибыли предприятия от реализации продукции. Выражение (2) - система специальных ограничений, в данном случае - на фактически имеющиеся объемы ресурсов. Выражение (3) - система общих ограничений на неотрицательность переменных.

В случае, если требуется решить задачу на минимизацию затрат на производство и реализацию продукции, целевая функция модели будет выглядеть так:

(4)

где: n - количество выпускаемых видов продукции;

c_j - затраты на производство и реализацию единицы j-й продукции;

x_j - объем выпуска j-го вида продукции.

Пример решения задачи:

Предприятие производит 2 вида продукции с использованием двух видов ресурсов - сырья и рабочей силы. Затраты ресурсов на изготовление 1 т каждого вида продукции и запасы ресурсов указаны в следующей таблице:

Ресурс	Расход ресурса на продукцию 1	Расход ресурса на продукцию 2	Запас ресурса
Сырье, т	3	5	120
Трудозатраты, ч	14	12	400

Прибыль, получаемая предприятием от реализации 1 т первого и второго вида продукции составляет соответственно 30 и 35 руб./т.

Требуется найти максимальную прибыль предприятия.

Решение:

Пусть x₁ - объем выпуска продукции вида 1 в тоннах, x₂ - объем выпуска продукции вида 2 в тоннах. Тогда задача может быть описана в виде следующей модели линейного программирования:

(5)

Такую задачу можно решить при помощи надстройки Поиск решения программы Microsoft Excel пакета Microsoft Office.

В целях нахождения решения задачи с помощью этого модуля необходимо предварительно составить в книге Microsoft Excel таблицу, содержащую исходные данные.

Для этого необходимо сначала загрузить программу Microsoft Excel, а затем внести в таблицу имеющиеся данные следующим образом:

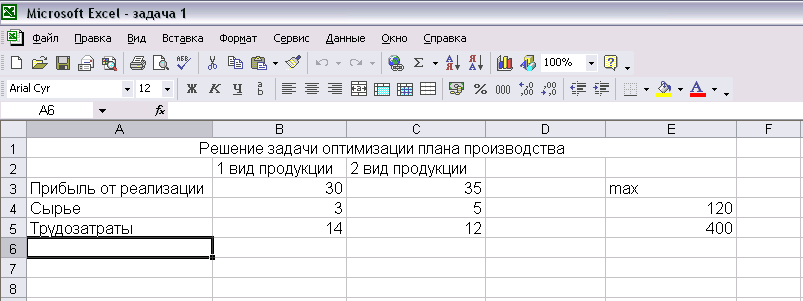
Рис. 1

Далее необходимо сохранить книгу под каким-либо именем, например, "задача 1.xls".

Добавим в таблицу еще одну строку (например, строку 6), в которую будут вноситься получаемые в ходе решения результаты. Объем выпуска продукции вида 1 будем предполагать получить в ячейке В6, продукции вида 2 - в ячейке С6, а искомую прибыль - в ячейке Е6.

Для решения задачи необходимо также выделить столбец (в данном примере - столбец D), в который будут введены формулы для расчета значений левой части ограничений. Формула вводится также и в ячейку, в которой будет рассчитана прибыль предприятия (ячейка Е6). Нужно обратить внимание на то, что в формулах используются не числа или символьные обозначения, а координаты ячеек таблицы, в которых хранятся эти числа и переменные.

Рис. 2

Для запуска процедуры оптимизации в меню Сервис необходимо выбрать пункт Поиск решения.

В поле Установить целевую ячейку вводятся координаты ячейки (Е6), которую необходимо максимизировать, минимизировать или установить равной какому-либо числу. Поле нужного варианта оптимизации необходимо выделить указателем.

В поле Изменяя ячейки вводятся координаты ячеек (разделенные запятыми или объединенные в интервал двоеточием), в которых содержатся значения переменных - объемов выпуска продукции вида 1 и вида 2. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Можно использовать автоматический поиск таких ячеек с помощью кнопки Предположить.

В поле Ограничения необходимо ввести все граничные условия задачи:

Рис. 3

При этом ограничения на неотрицательность переменных можно ввести путем установки флажка Неотрицательные значения в окне Параметры. В случае, если решаемая задача является задачей линейного программирования, лучше отметить это в окне Параметры соответствующим флажком:

Рис. 4

Запуск процесса оптимизации производится нажатием кнопки Выполнить. По окончании счета появляется диалоговое окно Результаты поиска решения. Нажав в нем соответствующую кнопку, можно сохранить найденное решение или восстановить исходные значения. Изменения при этом коснутся как целевой ячейки, так и влияющих ячеек. В этом же диалоговом окне можно указать необходимые типы отчетов, которые будут размещены на отдельных листах книги.

Отчет Результаты отражает исходные и результирующие значения целевой и влияющих ячеек, а также сведения о наложенных ограничениях.

Рис. 5

Отчет Пределы отражает наибольшее и наименьшее значения влияющей ячейки при фиксированных и удовлетворяющих всем ограничениям остальных.

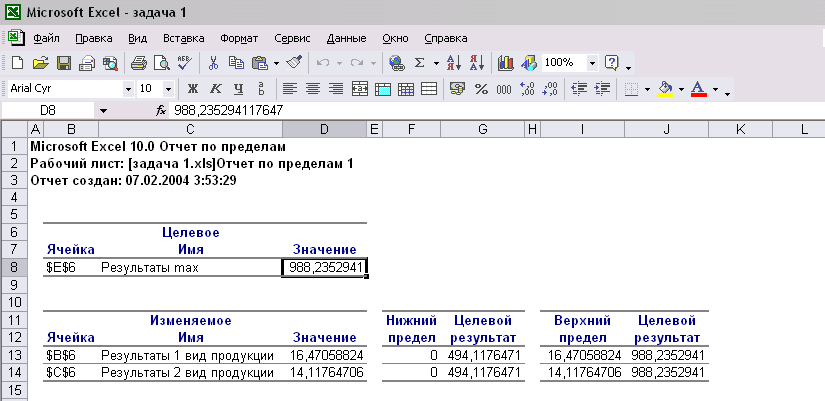
Рис. 6

Отчет Устойчивость содержит информацию о двойственных оценках для каждого ограничения, а так же о границах устойчивости по значениям коэффициентов целевой функции и правых частей ограничений.

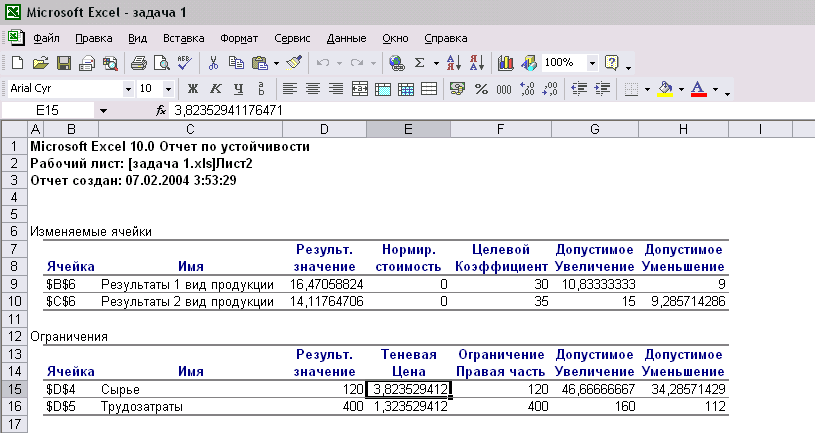
Рис. 7

В рассматриваемом примере двойственные оценки 1-го и 2-го видов ресурсов составляют соответственно 3,82 и 1,32. Это означает, что при увеличении запаса первого ресурса на 1 т максимальное значение целевой функции увеличится на 3,82 тыс. руб., при увеличении на 1 т запаса второго ресурса - на 1,32 тыс. руб.

Поскольку допустимое уменьшение коэффициента целевой функции 1-го вида продукции составляет 9 тыс. руб., а его допустимое увеличение - 10,83 тыс. руб., границы устойчивости по этому коэффициенту составляют интервал от 21 до 40,83 тыс. руб. Это означает, что если прибыль, получаемая от реализации 1 т продукции вида 1, будет являться любым числом, принадлежащим этому интервалу, количество этого вида продукции в оптимальном плане не изменится.

Таким же образом можно определить границы устойчивости по имеющимся количествам ресурсов: если количество второго ресурса (трудозатрат) попадет в интервал от 288 до 560 часов, двойственная оценка этого ресурса не изменится.

При необходимости, установив флажок Показывать результаты итераций в окне Параметры, можно приостанавливать процесс оптимизации после каждой итерации и просматривать ее результаты. Окно Параметры позволяет варьировать также максимальное время, предельное число итераций, относительную погрешность, допустимое отклонение, тип модели, метод поиска и т.д. Такая необходимость может возникнуть в случае, если по каким-либо причинам найти оптимальное значение целевой ячейки сразу не удается.

Полученные результаты решения рассматриваемой задачи выглядят так:

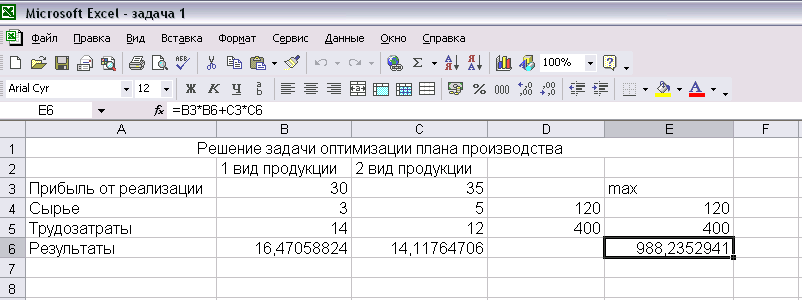
Рис. 8

Итак, максимальная прибыль предприятия будет составлять 988,24 тыс. руб. Для ее достижения предприятию необходимо производить 16,47 т продукции вида 1 и 14,12 т продукции вида 2.

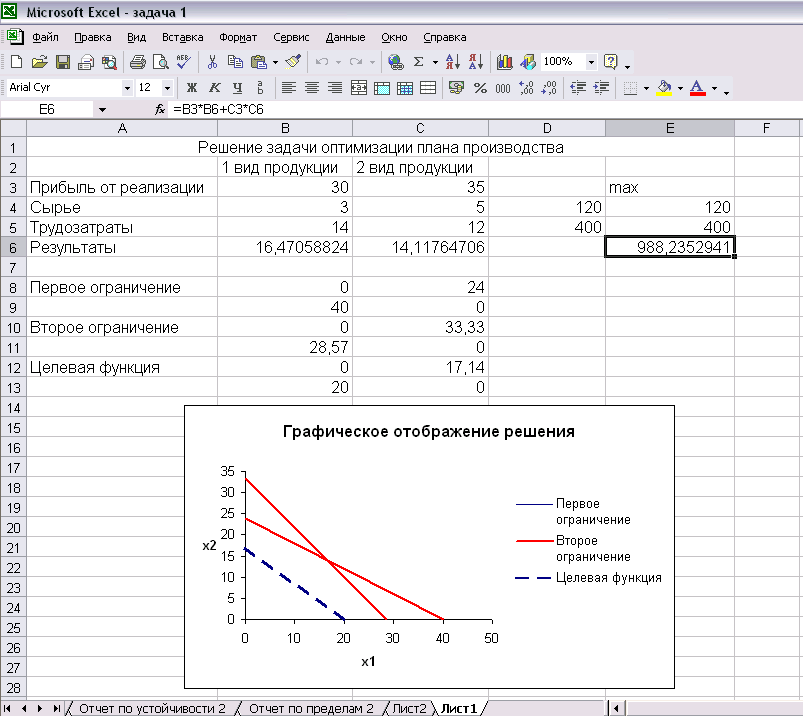
Рис. 9

Не менее удобным представляется решение этой задачи с помощью математической системы Mathcad, поскольку эта система позволяет оперировать привычными символами и формами записи математических выражений.

Для этого, запустив указанный программный продукт, необходимо в открывшемся окне документа набрать математическую модель задачи, которая для данного примера будет выглядеть так:

Рис. 10

В первой строке записано выражение для нахождения значения целевой функции F (x₁, x₂). Знаком ":=" в системе Mathcad обозначается оператор присваивания левой части функции или уравнения значения ее правой части. В отличие от него, знак "=" используется в системе Mathcad только для вывода результатов вычислений.

Вторая и третья строка обуславливают присвоение переменным x₁ и x₂ их начальных значений.

Блок ограничений в системе Mathcad открывается служебным словом Given. Далее записываются все ограничения, накладываемые на переменные условиями задачи.

В целях нахождения искомого решения задачи необходимо выбрать из списка функцию Maximize и ввести требуемые аргументы (см. рис. 11). После ввода знака выполнения вычислительных операций получим значения аргументов функции, при которых функция достигает максимума при данных условиях.

Для получения максимального значения функции нужно присвоить переменным полученные значения и выполнить процедуру вычисления. Система позволяет получить и графическое отображение решения задачи.

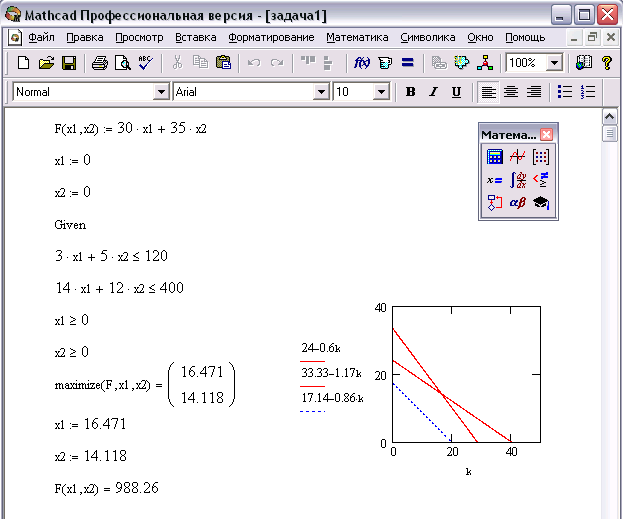
Рис. 11

Сплошной линией на рисунке отражены ограничения, а пунктирной - линия уровня целевой функции.

Задачи

Задача 1.1

Малое предприятие занимается сборкой мебели из поступающих комплектующих. В настоящее время на предприятии собирают шкафы - двух- и трехстворчатые, которые затем продаются по 3 тыс. руб. и 4 тыс. руб. соответственно.

Каждый шкаф собирается из основы, полок и дверцей. На двухстворчатый шкаф требуется 1 основа вида "А", 2 дверцы и 10 полок, на трехстворчатый - 1 основа вида "Б", 3 дверцы и 15 полок. Всего на складе имеется 110 основ вида "А", 100 основ вида "Б", 400 дверцей и 2000 полок.

Какую максимальную прибыль может извлечь предприятие от продажи собранных шкафов?

Задача 1.2

Цех хлебозавода по производству муки заключил контракт с мини-пекарней о поставке ежедневно 300 кг ржаной и пшеничной муки, причем пшеничной - не менее 50%. Зерно, поступающее в цех, проходит в нем обмолот, помол и упаковку муки. Трудозатраты (в человеко-часах) на указанные операции представлены в таблице:

Операция	Ржаная мука	Пшеничная мука	Имеющийся ресурс
Обмолот	0,1	0,1	30
Помол	0,1	0,08	27
Упаковка	0,05	0,05	200

Себестоимость одного килограмма ржаной муки составляет 14 рублей, а пшеничной - 18 рублей.

Требуется найти оптимальный план производства продукции, позволяющий цеху выполнить условия контракта с наименьшими затратами.