Теоретический материал

В общем виде мостовой схемой называют цепь, четырехполюсник или многополюсник, коэффициент передачи которой при определенных условиях равен нулю. Эти условия называют условиями баланса или равновесия моста. Ветви цепи, сопротивления которых входят в условия равновесия, называют плечами моста. В зависимости от числа плеч, входящих в схему моста, последний может быть четырехплечным, шестиплечным и т.д. в случае мостов переменного тока условия равновесия связывает комплексные сопротивления плеч. В тех случаях, когда в уравнение баланса моста переменного тока не входит частота, говорят о частотно-независимых мостах.

Мостовые схемы широко применяются в измерительной технике для определения сопротивлений, емкости, индуктивности, частоты. На основе мостовых схем строятся приборы для измерения напряжения, мощности, температуры и т.п. широкое применение мостовых схем объясняется их большой точностью, высокой чувствительностью и относительной простотой.

Основное уравнение моста. Схема наиболее распространенного одинарного четырехплечного моста изображена на рисунке 4.1, где Z₁ ... Z₄ – плечи моста, АВ – диагональ питания, CD – индикаторная диагональ. Баланс моста характеризуется отсутствием напряжения между точками С и D при наличии напряжения в точках АВ.

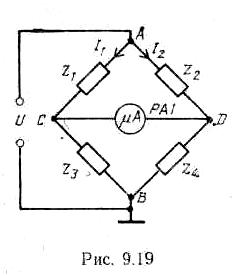
Рис. 4.1 Одинарный измерительный четырехплечный мост

Напряжение на сопротивлении Z₃ в момент баланса моста равно напряжению на Z₄ , т.е. I₁Z₃ = I₂Z₄, а значение токов

и

откуда , или

Z₂ Z₃ + Z₃ Z₄= Z₁ Z₄ + Z₃ Z₄ .

Окончательно уравнение баланса четырехплечного баланса моста записывается так:

Z₂ Z₃ = Z₁ Z₄ ,

т.е. произведения сопротивлений противоположных плеч моста равны.

Учитывая, что плечи моста – комплексные сопротивления, т.е. Z = R + jХ = z e^jφ, равенство Z₂ Z₃ = Z₁ Z₄ можно представить

z₂ z₃ e ^j(φ₂^{+ φ}₃⁾ = z₁ z₄ e ^{j(φ1+ φ4),}

отсюда z₂z₃ = z₁z₄ и φ₂ + φ₃ = φ₁ + φ₄ , т.е. произведение модулей сопротивлений и сумма величин фазовых сдвигов противоположных плеч равны.

Чувствительность мостовой схемы. Допустим, что сопротивление одного из плеч моста изменилось на величину Δz. Обозначим через Δu_и измерение напряжения в измерительной диагонали, вызванное изменением сопротивления плеча. Отношение S_ср = Δu_ин / ΔZ называют средней чувствительностью моста, а предел этого выражения при Δz→0 называют чувствительностью мостовой схемы в точке Z: S = lim_Δz→0 (Δu_и /Δz). Чувствительность моста увеличивается с увеличением чувствительности измерительного прибора и с увеличением напряжения питания моста.

Мосты для измерения сопротивлений на постоянном токе. Схема моста постоянного тока не отличается от изображенной на рисунке 4.1. Плечи моста составлены из активных резисторов, их величина может изменяться ступенчато и плавно. Одно из плеч – измеряемое сопротивление. Например, Z₄ = R_x. В момент баланса моста (равенства нулю показаний прибора) в соответствии с уравнением баланса моста

Плечо, содержащее R₂, называют плечом сравнения, а плечи, содержащие R₃, R_1, - плечами отношения.

Большими чувствительностью и точностью при измерении алых сопротивлений обладают так называемые двойные мосты, в которых влияние соединительных проводов и контактов сведено к минимуму.

Погрешность мостового метода измерения определяется качеством изготовления образцовых резисторов и чувствительностью измерительного прибора, её можно значительно увеличить, применив электронный усилитель. При достаточной чувствительности индикатора максимально возможная погрешность δ_R , %, составит

δ_R = δ₁+ δ₂ + δ₃,

где δ₁, δ₂, δ₃ – погрешности изготовления или определения известных плеч.

В ряде случаев используют разбалансированный мост. Ток в измерительной диагонали при разбалансе определяется напряжением питания моста, сопротивлением прибора и величиной разбаланса. Выражение для тока разбаланса, определяется из законов Кирхгофа:

Оно может быть упрощено при небольших, менее 20%, значениях разбаланса:

,

где ΔR₄ – абсолютное отклонение величины сопротивления R₄ от значения, при котором мост сбалансирован; U – напряжение питания моста; R_и – сопротивление измерительного прибора.

Измерение параметров конденсаторов. Существует множество мостовых схем для измерения параметров конденсаторов. Измерения проводят, как правило, на низкой частоте (50 … 1000 Гц). В качестве индикатора баланса используют телефоны или электронный вольтметр. Одна из возможных схем представлена на рисунке 4.2.

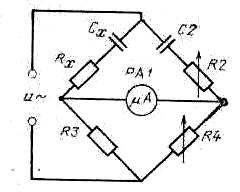
Рис. 4.2 Мост для измерения параметров конденсаторов

В этой схеме С_х – измеряемая ёмкость, R_x = R_п – сопротивление потерь исследуемого конденсатора. Условие баланса моста для данной схемы:

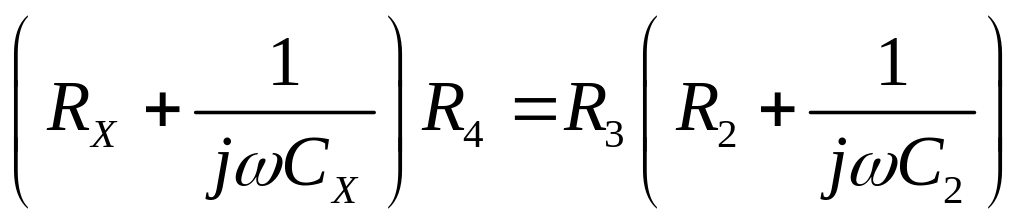
или

,

откуда R_x= R₂R₃ / R₄ и C_x = C₂ R₄ / R_3.

для балансировки моста служат резисторы R₂ и R₄ , выполненные в виде магазина сопротивлений. Магазин, изменяющий сопротивление R₄ , можно отградуировать непосредственно в значениях емкости (если С₂ и R₃ – величины постоянные), а магазин R₂ – в значениях tg δ – угла потерь конденсатора.

Измерение индуктивности. В схему моста для измерения параметров индуктивности катушек входят два плеча с активным сопротивлением, плечо с объектом измерения (комплексным сопротивлением) и плечо с реактивным сопротивлением, чаще всего в виде конденсатора переменной ёмкости (рис. 4.3).

Рис. 4.3 Мост для измерения параметров индуктивных катушек

Из условия баланса мостовой схемы с учетом того, что

Z₁ = R₁ / ( )

Z_x = , можно получить

,

откуда L_x = C₁ R₂ R₃ и

R_L = R₂ R₃ / R₁ ,

что свидетельствует о возможности раздельной балансировки моста и непосредственной оценки как величины L_x , так и R_L, причем регулировки взаимозаменяемы и позволяют быстро уравновесить мост. Для расширения пределов измерения один из резисторов R₂ или R₃ выполняется в виде магазина сопротивлений.

ВОПРОСЫ САМОКОНТРОЛЯ

1. Начертите мостовую схему измерения сопротивлений и запишите условие равновесия моста.

2. Напишите уравнение для вращающего момента логометра.