8. Циклические коды: определение, классификация, основные свойства и способы задания или построения.

Циклические коды являются подклассом в классе линейных блоковых кодов, удовлетворяющих определенным требованиям. Были предложены Прейнджом. Свое название данные коды получили по причине того, что основной операцией построения кодовых последовательностей (Fi(x)) является цикл, а точнее циклическая перестановка двоичных символов разрешенных кодовых последовательностей. На основе цикла обеспечивается как формирование код-вых последовательностей так и декодирование.

Циклическим кодом называется такой групповой линейный код, у которого в результате циклического сдвига кодовых символов в разрешенной кодовой комбинации на 1,2,…,k-1 разрядов формируются разрешенные кодовые комбинации. Циклический код может задаваться с использованием порождающей и проверочной матриц, порождающего и проверочного полиномов, а также корней порождающего полинома и остатков от деления.

Основные свойства циклических кодов:

1. Вес (w_к.п) разрешенной кодовой последовательности ≥ d₀;

2. Вес проверочной части w_пр.ч разрешенной кодовой последовательности ≥ d₀-1;

3. Сдвиг кодовых символов разрешенной кодовой последовательности влево или вправо на 1, 2,…, (k-1) символ вновь приводит к разрешенной кодовой последовательности. Если же при циклическом сдвиге всегда будет получатся новая кодовая последовательность, то такой код будет называться квазициклическим;

4. Разрешенная кодовая последовательность без ошибок F_р'(x) при делении на полином P(x) дает нулевой остаток, т.е. F_р'(x)/P(x)=R(x)=0 и R(x) не равно 0 – при наличии ошибок;

5. Сумма по модулю два символов 2, 3,…, (k-1) разрешенных кодовых последовательностей вновь образует разрешенную кодовую последовательность;

6. Двучлен вида xⁿ +1 должен делиться на порождающий полином P(x) без остатка (имеется в виду обычная операция деления многочленов);

7. Результат деления двучлена xⁿ+1 на образующий полином P(x) дает полином, который носит название проверочного полинома и обозначается как h(x), т.е. h(x)=(xⁿ+1)/P(x);

8. Если все операции над полиномами (кодовыми последовательностями) проводятся в двоичном поле Галуа (GF(2)), т.е. действия над коэффициентами полиномов осуществляется по модулю два, а умножение полиномов производитсяпо модулю образующего полинома P(x), то применение указанных операций не приводит к кодовым последовательностям, длина которых больше длины заданного кода, т.е. “n”;

Классификация циклических кодов:

1. Коды Хэмминга, как правило используемые для коррекции случайных ошибок;

2. БЧХ-коды – дальнейшее развитие кодов Хэмминга. Используются для коррекции случайных и пакетных ошибок;

3. Коды Файра. Используются для коррекции пакетных ошибок;

4. Коды Рида-Майлера. Исп-ся для коррекции ошибок (случайных и пакетных), а также для формирования сложных сигналов;

5. Коды Рида-Соломона. Исп-ся для коррекции модульных ошибок.

9. Классификация алгоритмов декодирования циклических кодов. Поясните сущность коэффициента энергетического выигрыша кодирования.

Циклические коды декодируются с помощью следующих алгоритмов:

1.мажоритарное

2. синдромное

Мажоритарное:

-Формирование системы разделенных проверок (СРП)

- Формирование системы связанных проверок (ССП)

- Формирование системы квазиразделенных проверок

СРП:

1. а_i символ должен входить во все проверки

2.а_j(i не=j) должен входить в проверки по одному разу

Кол-во уравнений: 2*t_исп+1=N

ССП:

1.а_i должен входить во все проверки

2.а_j(i не=j) должен входить в лямбда(коэффициент связности) проверок

коэффициент энергетического выигрыша кодирования:

q=(E/N0)*F*t=(Pc/Pш)*F*t=энергия сигнала/спектр. плотность мощности шума

выйгрыш от кодирования оценивается lg отношения энергия сигнала к спектр. плотности мощности шума, необходимым для обеспечения заданной вероятности ошибок в системе передачи без кодирования к аналогичному значению в системе с кодированием.

q1=(Pc/Pш)_БК*F*t

q2=(Pc/Pш)_К*F*t

ЭВК =10(lg (Р_с/Р_м) _Бк – lg(Р_с/Р_м)_к

10. БЧХ-коды: определение, способы построения, алгоритм декодирования, достоинства и недостатки.

Коды Боузе-Чоудхури-Хоквингема (БЧХ-коды) являются дальнейшим развитием линейных блоковых кодов Хэмминга, относятся к классу циклических кодов и обеспечивают коррекцию как независимых, так и группирующихся (пакетных) ошибок.

Циклический двоичный код длины n=2^ε–1 двоичных символов называется примитивным БЧХ-кодом с конструктивным кодовым расстоянием d=2·t+1, если его образующий полином равен P(x)=НОК[m₁(x), m₃(x), …, m_2t-1(x)], где m_i(x) – минимальный примитивный полином степени ε=log₂(n + 1). Максимальная степень P(x) и, следовательно, число проверочных символов не более l<ε·t_исп двоичных символов (t_исп – кратность исправляемых ошибок), а число информационных символов равно k=n–ε·t_исп двоичных символов.

Из определения БЧХ-кода следует, что корнями P(x) являются элементы α,α³,α⁵,…α^2tисп-1, а также α²,α⁴,α⁶,…α^2tисп, т.е. 2t_исп последовательных степеней α. Поэтому конструктивное кодовое расстояние кода равно 2t_исп+1.

БЧХ-коды могут задаваться с использованием порождающей и проверочной матриц, порождающего (образующего) и проверочного полиномов, а также корнями порождающего (образующего) полиномов.

Для того, чтобы выполнялось основное условие F’(x)∙H^T(x)=0, проверочная матрица БЧХ-кода должна иметь вид:

Алгоритм декодирования двоичных БЧХ-кодов, исправляющих все конфи­гурации ошибок кратности t (t>l) двоичных символов, состоит из выполнения трех этапов, а именно [3,7,8]:

-первый этап декодирования предусматривает вычисление каждого компонента синдрома S_i с нечетным номером путем деления принятой кодовой последовательности F_i(x) на минимальный полином m_j(x) элемента αⁱ и вычисление значения остатка от деления R_i(x) в точке х= αⁱ: S_i=F(αⁱ)=R(αⁱ);

-второй этап декодирования предусматривает по полученному синдрому определение полинома локаторов ошибок вида,

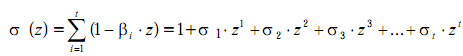
-третий этап декодирования включает коррекцию ошибок при условии, что кратность ошибок не превосходит значения t и номера позиций искаженных ин­формационных символов обратны корням полиномов (z).

При декодировании БЧХ-кодов сложность схем коррекций при t≥3 резко возрастает. Поэтому коррекция многократных ошибок с помощью БЧХ-кодов на практике используется достаточно редко.

11. РС-коды: определение, способы построения, основные параметры, алгоритмы декодирования и области применения.

Коды Рида–Соломона.

Коды, имеющие следующую структуру:

H=[hⁱ h²ⁱ h³ⁱh ⁴ⁱ…].

H_БЧХ=[aⁱ a³ⁱ a⁵ⁱa⁷ⁱ…].

РС-коды являются частным случаем БЧХ-кодов, но обеспечивают минимальную избыточность.

РС – не двоичные, групповые, циклические коды, которые задаются порождающим полиномом следующего вида P(x)=(x-a^j0)(x-a^j1)… (x-a^j+2t-1)

(x-a^ij) – двучлен определяющий максимальную длину кодовой последовательности

t – кратность исправляемых ошибок

На практике широкое применение для задания РС кода, получили проверочная матрица

Н(x)= [ h⁰ h¹ h² … h^f I_В 0] I_В – единичная проверочная матрица

[ h⁰ h² h⁴ … h^2f 0 I_В]

Код Рида — Соломона над  , исправляющий   ошибок, требует   проверочных символов и с его помощью исправляются произвольные пакеты ошибок длиной   и меньше. 

Код (РС) — это очень эффективный и удобный в реализации (k, N)-блочный код, позволяющий обнаруживать и исправлять ошибки в байтах. Входным словом для него является блок из k байтов, выходным — кодовое слово из N байтов, состоящее из k исходных и N-k проверочных байтов. При этом гарантировано, что при декодировании в кодовом слове будут обнаружены и исправлены t=(N-k)/2 байтов независимо от их расположения внутри кодового слова. Параметр t - корректирующая способность кода. Кодер РС реализуется на основе регистра сдвига с 2t байтовыми элементами памяти и обратными связями. Процесс кодирования сводится к операциям сложения и умножения по модулю 256.

Основные параметры

1) n= t _m *(2^ t _m + 1) бит (длина кодовой комбинации)

2) к= t _m *(2^ t _m – 1) бит (информационный символ)

3) d₀ = n-k+1(минимальное кодовое расстояние)

4) L=2* t _m +1 (количество проверочных символов)

Формирование кодовой комбинации

F(x)=Q(x)*G(x)

Q(x)=x^(k-1)+ x^(k-3)+…+1

S(x)=F’(x)*H^T(x)

Область применения: обеспечивает коррекцию пакетных ошибок,

Данные коды являются подмножеством БЧХ-кодов и задаются с помощью порождающего полинома:

, i – любое, t – кратность корректируемого модуля ошибок.

• Например, найдем для (15;11) PC-кода с над . Пусть , тогда .

Следовательно, r=n-k=4, k = 11 из , что эквивалентно 44 двоичным символам, а все кодовое слово является набором из 60 бит.

• Пусть , найдем для PC-кода (7;3) с над . Тогда

.

Информационный многочлен – последовательность восьмеричных символов (что эквивалентно девяти битам).

Предположим, что .

В этом случае кодовое слово неразделимого циклического кода имеет вид

что представляет собой последовательность семи восьмеричных символов (73=21 бит).

Кодирование и декодирование циклических PC-кодов осуществляется так же, как и БЧХ-кодов, и реализуется на основе регистров сдвига без и с обратными связями.

Алгоритм декодирования циклического кода, исправляющего одиночные пакеты ошибок длины , состоит в следующем.

1. Вычисляется синдром принятого сообщения .

2. Если – считаем, что ошибок не произошло.

3. При , .

4. Определяется степень многочлена .

5. Если , то считаем, что многочлен ошибок , и производится операция коррекции .

6. Если , то вычисляем и переходим к п.4 с .

Коды Рида–Соломона

Коды Рида–Соломона (PC-коды) получили широчайшее применение в различных системах передачи и хранения информации, особенно в качестве подкодов каскадных кодов для контроля зависимых ошибок.