5. Проверочная матрица группового кода: определение, назначение, классификация, основные свойства и ее взаимосвязь с порождающей матрицей.

Проверочная матрица H(x) представляет собой сокращенную форму записи кода, а именно количество строк H(x) определяет длину проверочных символов l. Количество столбцов H(x) определяет длину кодовой комбинации n.

Проверочная матрица H(x) позволяет выполнить систему проверок, а также определяет алгоритм декодирования.

В общем виде проверочная матрица может быть записана так:

Проверочная матрица H(x) в основном используется при декодировании по правилу:

где S(x)- двоичный вектор размерности (длины) l двоичных символов, который носит название синдрома: (синдром- это совокупность признаков, а для ЛКБК синдром – это совокупность нулевых и ненулевых символов). Если S(x)=0, то это означает отсутствие ошибок в принятой кодовой комбинации.

Основные свойства H(x):

- количество ненулевых символов в каждой строке должно быть не менее d₀;

- количество ненулевых символов в каждом столбце должно быть ≥ t_исп;

- проверочная матрица H(x) не должна иметь двух одинаковых строк или столбцов;

- G^T(x)*H(x)=H^T(x)*G(x)=0.

Пример:

b₁ =a₂+ a₃+ a₄

b₂ =a₁+ a₃+ a₄

b₃ =a₁+ a₂+ a₄

F(x)=1001 100

F’(x)=1101 100

S’(x)=F’(x)∙H^T(x)

F’(x)=1101 100

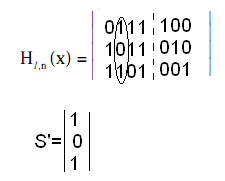
F’(x)=1001 100

S’(x)=0 нет ошибок

S’(x)≠0 есть ошибка

(6-7) 6. Порождающие полиномы групповых кодов : определение, назначение и взаимосвязь их с проверочными полиномами. 7 Проверочные полиномы групповых кодов: определение, назначение и взаимосвязь их с порождающими полиномами.

Код называется групповым, если кодовые комбинации образуют некоторую подгруппу группы всех последовательностей длины n.

Порождающие и проверочные полиномы – неприводимые примитивные полиномы, которые обладают свойством не разложения на полиномы меньшей степени и делятся только на самих себя или на единицу.

Порождающий полином должен быть неприводимым и примитивным(при делении принятой последовательности на проверочный полином давать n ненулевых остатков).

Порождающие полиномы в основном используются для формирования кодовых последовательностей. Проверочные полиномы могут использоваться как для формирования кодовых последовательностей, так и для декодирования.

P(x)=x^l+x^l-1+…1 - порождающий полином;

h(x)=x^l-1+x^l-2+…1 - проверочный полином.

P(x)*h(x)=xⁿ+1.

Проверочный полином можно получить из порождающего следующим путем:

. (Используется деление нацело)

При использовании порождающих полиномов могут использоваться разделимые и неразделимые кодовые комбинации.

Для неразделимой кодовой комбинации используется выражение:

F(x)=Q(x)*P(x), где Q(x) - блок передаваемых информационных символов в виде полинома, F(x) - полученная кодовая комбинация, P(x) - порождающий полином.

Для разделимой кодовой комбинации делаются следующие преобразования:

1) умножаем на , т.е. сдвигаем на l разрядов влево

2) деление , где R(x) – остаток от деления;

3) тогда кодовая комбинация: F(x)=

где Q(x) - блок передаваемых информационных символов в виде полинома, F(x) - полученная кодовая комбинация, P(x) - порождающий полином, =R(x) - проверочные символы.

В качестве примеров можно самому придумать 2 полинома Q(x) и P(x) и сформировать разделимую и неразделимую кодовую последовательности соответственно согласно формулам.