3. Умовний екстремум при обмеженнях типу рівність.

Нехай дано двічі безперервно диференційовні цільова функція f(х) і функції обмежень g_j(x) визначають безліч припустимих рішень U.

Потрібно досліджувати функцію f(x) на екстремум

(8)

де .

Стратегія вирішення задачі

Означення 8.

Функція зветься узагальненою функцією Лагранжа, числа – множники Лагранжа.

Класична функція Лагранжа має вигляд .

Означення 9.

Градиєнтами узагальненої та класичної функцій Лагранжа по х є вектор-стовпець з частинними похідними першого порядку

, .

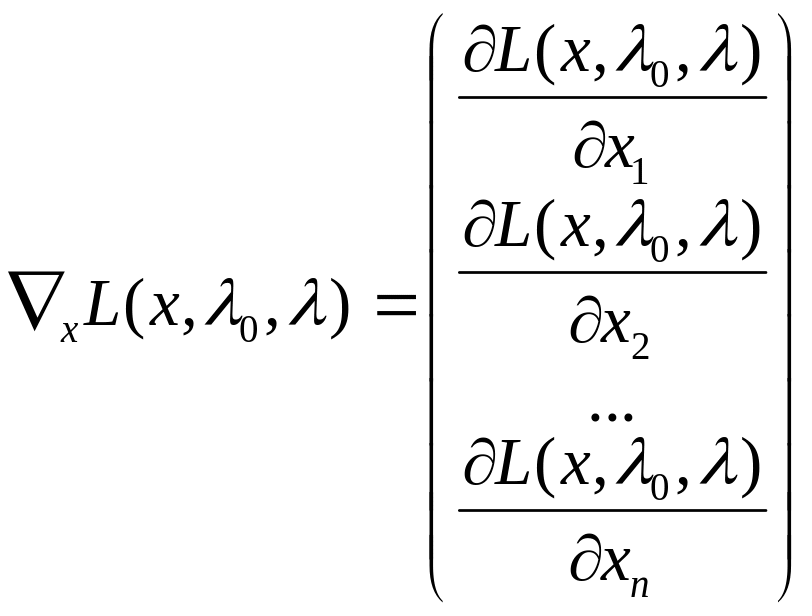Означення 10.

Другим диференціалом узагальненої та класичної функцій Лагранжа є

, .

Означення 11.

Першим диференціалом обмежень g_j(x) є функція

.

Приклад 7.

Записати функції Лагранжа для задачі пошуку екстремуму функції на множені , на заданому обмеженні

Необхідні умови екстремуму першого порядку при обмеженнях типу рівність.

Нехай точка х^* - точка локального екстремуму в задачі (8). Тоді знайдуться такі числа не рівні одразу 0 і такі, що виконуються умови:

(9.1)

(9.2)

Якщо при цьому градієнти в точці х^* лінійно незалежні, то (умова регулярності).

Система (8) має (m+n) рівнянь з (m+n+1) невідомими . Точки які задовольняють системі (9) звуться умовно стаціонарними.

При вирішенні задачі (8) перевірка умови регулярності утруднена, тому що точка х^* заздалегідь невідома. Тому розглядають два випадки:

1.

2. .

Якщо , то вважають, що . Це еквівалентно діленню системи рівнянь (9) на та заміні на . При цьому узагальнена функція Лагранжа становиться класичною функцією а сама система (9) приймає вигляд

(10.1)

(10.2)

Означення 12.

Точка екстремуму, яка задовольняє системі (9) при зветься регулярною, а при нерегулярною. При цьому в узагальненій функції Лагранжа відсутній член, який відповідає за цільову функцію, а необхідних умовах екстремуму не використовується інформація яка представлена градієнтом цільової функції.

Необхідні умови екстремуму другого порядку

при обмеженнях типу рівність.

Нехай х^* - регулярна точка мінімуму (максимуму) в задачі (8) та мається рішення цієї системи. Тоді другий диференціал класичної функції Лагранжа, обчислений в точці не від'ємний (не позитивний):

для всіх таких, що

Достатні умови екстремуму другого порядку

при обмеженнях типу рівність.

Нехай є точка в якій виконуються умови (10). Якщо в цій точці >0 (відповідно <0), для усіх не нульових dx таких, що

, то точка х^* є точкою локального мінімуму (максимуму).

Алгоритм вирішення задачі

1. Складаємо узагальнену функцію Лагранжа

2. Виписуємо необхідні умови екстремуму першого порядку

а) б)

3. Вирішуємо систему рівнянь для двох випадків

а). б) ( ).

4. Для точок перевіряємо достатні умови екстремуму:

а) записуємо другий диференціал класичної функції Лагранжа в точці

б) записуємо систему додаткових умов з системи обмежень в точці х^*

в) з останніх умов виділяємо любі m диференціалів dx_i через останні (m-n) та підставляємо їх в диференціал .

г) якщо >0 при не нульових dx, то в точці х^* умовний локальний мінімум;

якщо <0 при не нульових dx, то в точці х^* умовний локальний

максимум.

Якщо виконання додаткових умов не виконуються, слід провести виконання додаткових умов другого порядку. Якщо вони виконуються, то треба проводити додаткові дослідження, в противному випадку в точці х^* екстремуму немає.

3. Обчислення значення цільової функції в точці умовного екстремуму.

Результати досліджень локальних екстремумів в точці х^* приводимо у таблиці 1.

Таблиця 1.

№			Тип умовно-стаціонарної точки х*
1	>0	0,	Умовний локальний мінімум
2	<0	0,	Умовний локальний максимум
3	≥0	0	Може бути умовний локальний мінімум. Необхідні додаткові дослідження.
4	≤0	0	Може бути умовний локальний максимум. Необхідні додаткові дослідження.
5	=	0	Необхідні додаткові дослідження.
6	>0, <0	0	Екстремуму немає.

Приклад 8.

Знайти при обмеженнях .