Питання для самоконтролю.

• Сформулюйте задачу дробово-лінійного програмування.

• Дайте економічну інтерпретацію задачі дробово-лінійного програмування.

• Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування.

• У чому принципова відмінність геометричної інтерпретації задачі дробово-лінійного програмування?

• Навколо якої точки здійснюється поворот лінії рівня?

• Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування графічним методом.

Тема 6. Нелінійні оптимізаційні моделі економічних систем Лекція 8 Тема лекції: Задачі нелінійного програмування

Мета: ознайомити студентів з методами розв’язання задач нелінійного програмування.

План лекції

1. Постановка задачі пошуку екстремуму функції.

2. Властивості випуклих множин та випуклих функцій.

3. Необхідні та достатні умови безумовного екстремуму функції.

4. Умовний екстремум при обмеженнях типу рівність.

Література:

1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.

2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.

3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.

4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.

1. Постановка задачі пошуку екстремуму функції.

Знайти такий вектор , що належить області допустимих рішень цільова функція від якого

Зауваження:

1. Пошук максимуму функції зводиться до задачі визначення мінімуму функції шляхом заміни знака перед функцією на протилежний:

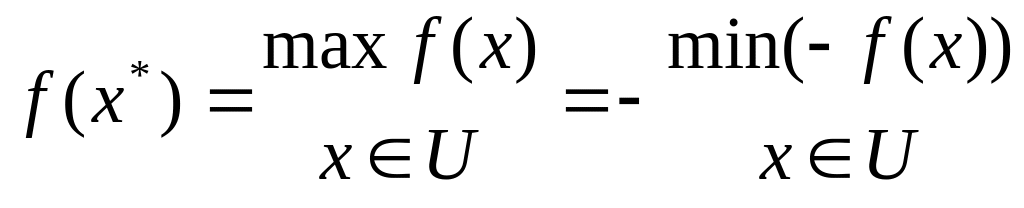
2. Задача пошуку максимуму та мінімуму цільової функції зветься задачею пошуку екстремуму:

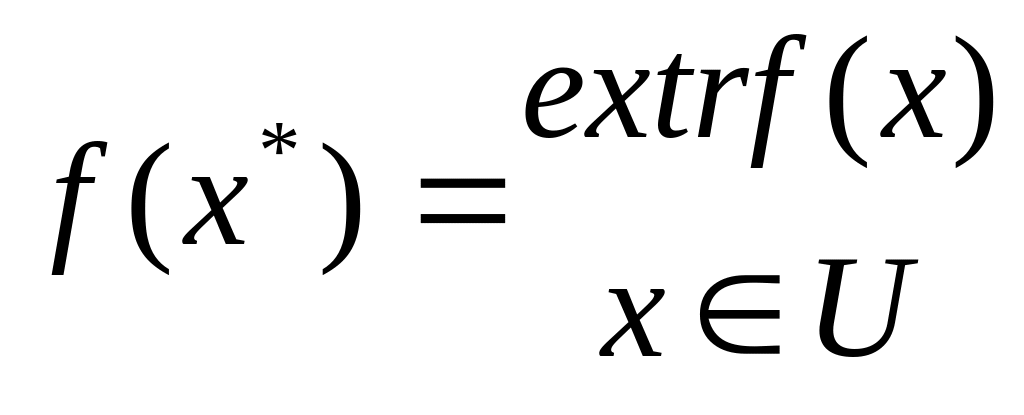
3. Якщо безліч допустимих рішень U задається обмеженнями, що накладаються на вектор х, то вирішується завдання пошуку умовного екстремуму. Якщо, обмеження на вектор х відсутні, то вирішується завдання пошуку безумовного екстремуму.

4. Рішенням задачі пошуку екстремуму є пара 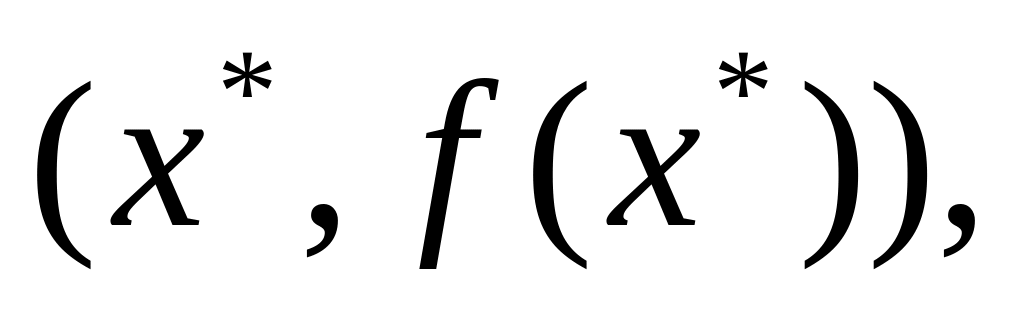яка включає точку х^* та значення цільової функції f в цій точці.

Нагадаємо, що точка зветься точкою глобального мінімуму (або просто мінімуму), якщо на множені U функція досягає свого мінімального значення, тобто

точка зветься точкою локального мінімуму функції f на множені U, якщо >0, що < то

Тут - евклідова норма вектора х.

Загальна задача нелінійного програмування полягає у знаходженні максимального(мінімального) значення функції

Z=f(x₁, x₂,….. x_n) →max/ min (1)

за умов

g_i(x₁, x₂,….. x_n) { ≤=≥}b_i, i=1,2…..m (2)

де всі функції (або їх частина) нелінійні.

Функція f з (1) – цільова функція, а умови g_i з (2) - умовами обмеження.

Сукупність змінних, що задовольняють обмеженням (2) задачі називається допустимим розв’язком або планом. Кожному допустимому розв’язку відповідає певне значення цільової функції.

Допустимий розв’язок (план), при якому цільова функція набуває найбільшого (найменшого) значення називається оптимальним планом. Найбільше (найменше) значення функції в допустимій області розв’язків називається глобальним максимумом (мінімумом).

Означення 1. Поверхнею рівня функції f(х) називається множина точок, в яких функція приймає постійне значення, тобто f(х)=const. Якщо n=2, то поверхня рівня зображується лінією рівня на площині R².

Приклад 1. Побудувати лінію рівня функцій:

a)

b)

c) .

Означення 2. Градієнтом безперервно диференційованої в точці х функції f(х) зветься вектор - стовпець, елементами якого є часткові похідні першого порядку, обчислені в точці х:

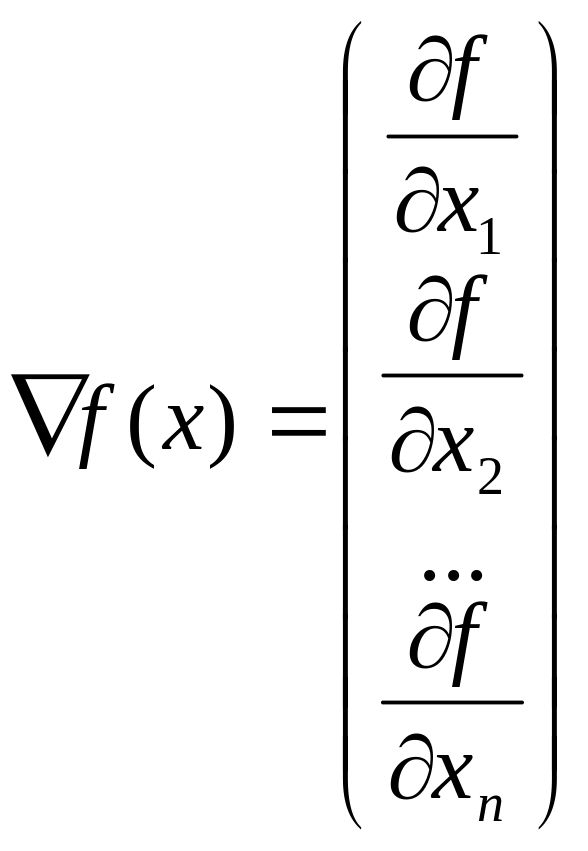
Градієнт функції направлений по нормалі до поверхні рівня, тобто перпендикулярний до дотичної площини, проведеної в точці х, у бік найбільшого зростання функції в даній точці.

Означення 3. Матрицею Гессе Н (х) двічі неперервно диференційованою в точці х зветься матриця часткових похідних другого порядку, обчислених в точці:

Н= =

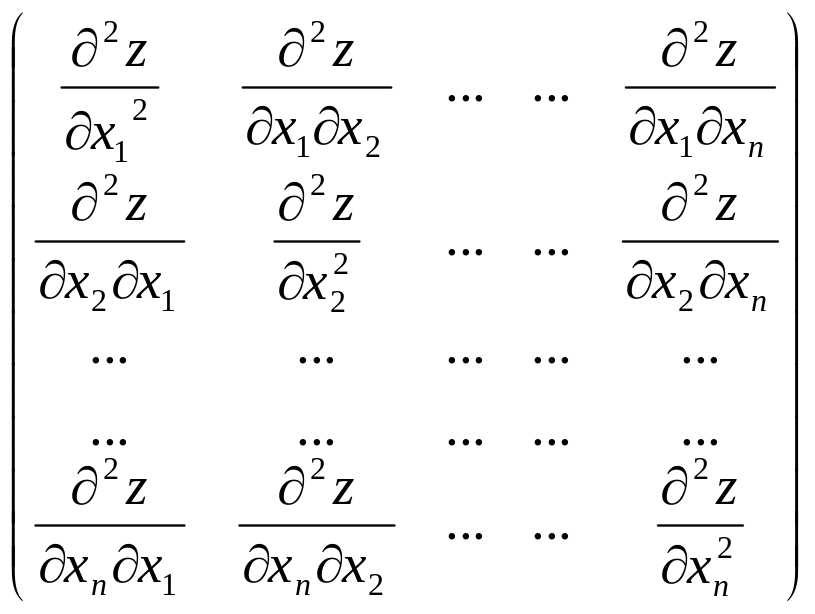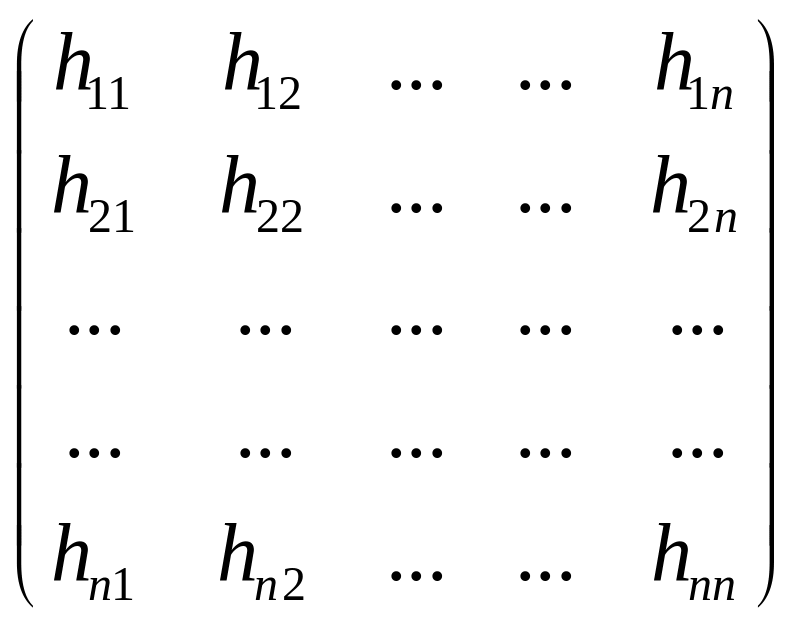
Зауваження:

1. Матриця Гессе є симетричною матрицею розміром nxn.

2. Разом з градієнтом можна визначити вектор антіградіента, рівний за модулем вектору градієнта, але протилежного за напрямком. Він вказує у бік найбільшого спуску функції в даній точці.

3. За допомогою градієнта та матриці Гессе, використовуючи розкладання в ряд Тейлора, приріст функції f(x) може бути записано у формі:

(2)

де - сума всіх членів розкладання в ряд Тейлора, які мають порядок вище другого, - квадратична форма.

Приклад 2.

Знайти значення градієнта функції в точках та матрицю Гессе.

Зауважемо, що в цьому прикладі матриця Гессе від функції не залежть від змінної х.

Приклад 3.

Для функції знайти градієнт та матрицю Гессе в точках .

Означення 4.

Квадратична форма (та відповідна їй матриця Гессе Н(х)) зветься:

• додатньо визначеною (Н(х)>0), якщо для будь-якого ненульового Δх виконується нерівність 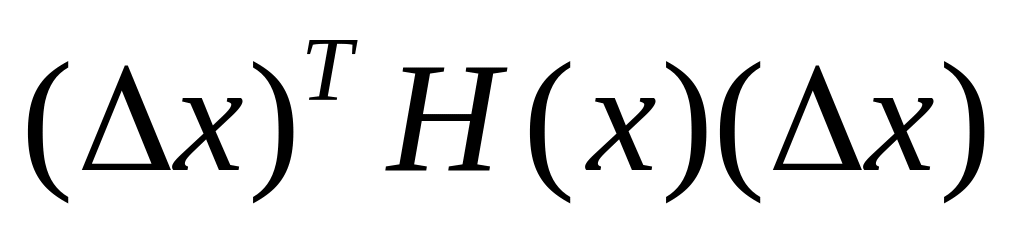>0;

• від’ємна визначеною (Н(х)<0), якщо для будь-якого ненульового Δх виконується нерівність 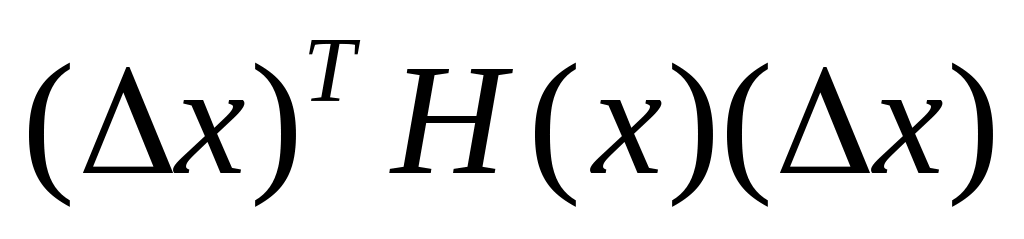<0;

• додатньо напіввизначеною (Н(х)≥0), якщо для будь-якого ненульового вектора Δх виконується нерівність ≥0 і є відмінний від нуля вектор Δх, для якого =0;

• від’ємно напіввизначеною (Н(х)≤0), якщо для будь-якого ненульового вектора Δх виконується нерівність ≤0 і є відмінний від нуля вектор Δх, для якого =0;

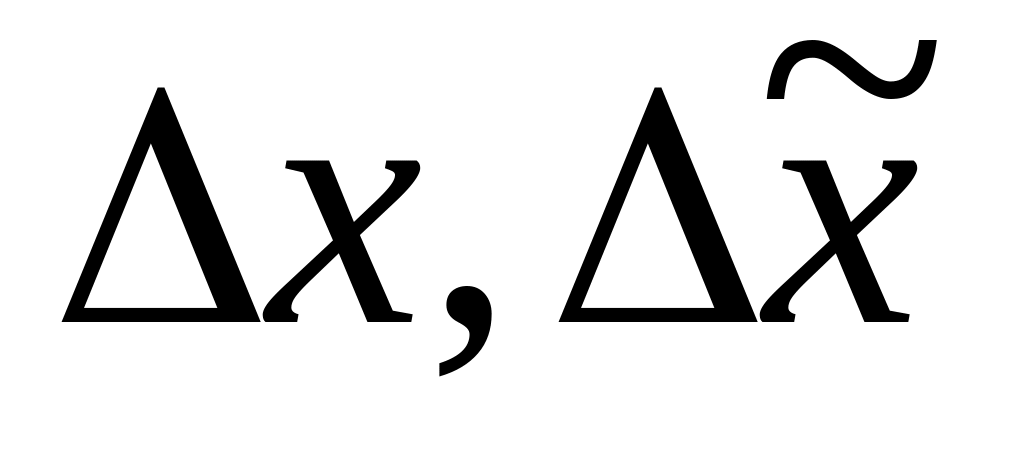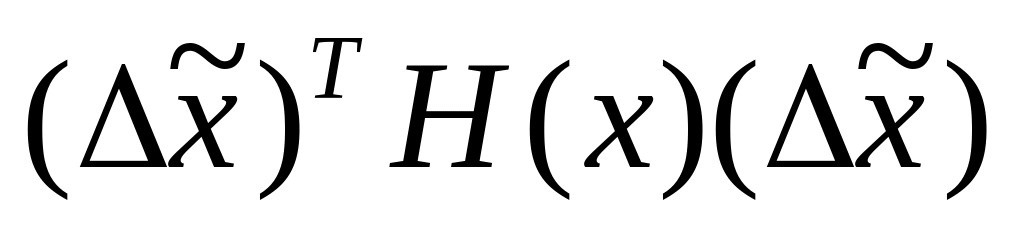• невизначеною, якщо існують такі вектора , що виконуються нерівності >0, <0;

• тотожньо рівною нулю (Н(х)≡0), якщо для будь-якого вектора Δх виконується рівність =0.

Приклад 4.

Класифікувати квадратичні форми та матриці Гессе:

а) ; б) ; в) .

Задачі НП розв’язуються значно складніше, ніж задачі ЛП. Для відшукання їх розв’язків немає універсального методу.

Лише для небагатьох типів задач НП розроблені обчислювальні методи їх розв’язання.

Найбільш вивчені задачі з нелінійною цільовою функцією певного виду і лінійними обмеженнями. Для розв’язання таких задач використовується ідея зведення до лінійного вигляду, що допускає застосування симплексного методу. Ще однією особливістю задач НП є наявність точок оптимуму, які можуть бути як граничними, так і внутрішніми точками області допустимих розв’язків.

Як згадувалось вище, найбільш вивченими є задачі з нелінійною цільовою функцією і лінійними обмеженнями, які можна класифікувати таким чином:

• Задачі дробово-лінійного програмування

Z=(∑c_ix_i)/( ∑d_ix_i) →max/ min

за умов

∑a_ijx_j =b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

• Сеперабельна задача НП

f(x₁, x₂,….. x_n) =∑f_i(x_i) →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

• Квадратична задача НП

f(x₁, x₂,….. x_n) =∑c_jx_j +∑∑d_jix_ix_j →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

Рішення задач мінімізації (максимізації) в Rⁿ, як правило, ускладнюються. Деякі з цих труднощів зникають, якщо розглядати тільки випуклі (вгнуті) цільові функції.