4. Графічне розв’язання задачі дробово-лінійного програмування.

У загальному випадку цільова функція задачі дробово-лінійного програмування має вигляд

(13)

З огляду на те, що , тобто , можна записати

(14)

З рівняння (13) виразимо змінну х₂ через х₁

(15)

або

(16)

Останнє рівняння можна розглядати як рівняння прямої з кутовим коефіцієнтом . З виду k можна зробити висновок, що при зміні значення цільвої функції z, змінюється k- кут нахилу лінії рівня. На відміну від задачі ЛП, щоб досягти оптимального значення z, лінію рівня потрібно повертати, а не переміщувати паралельно самій собі. Залишилося з’ясувати два питання:

• як повертати: за годинковою стрілкою або проти годинкової стрілки;

• навколо якої точки здійснювати поворот.

Звернемо увагу на те, що

. (17)

Кутовий коефіцієнт є функцією z. Щоб визначити, як повертати лінію рівня для досягнення z_max або z_min, необхідно дослідити функцію k(z) на монотонність.

Обчислемо похідну

(18)

• якщо то k зростає при збільшенні z;

• якщо 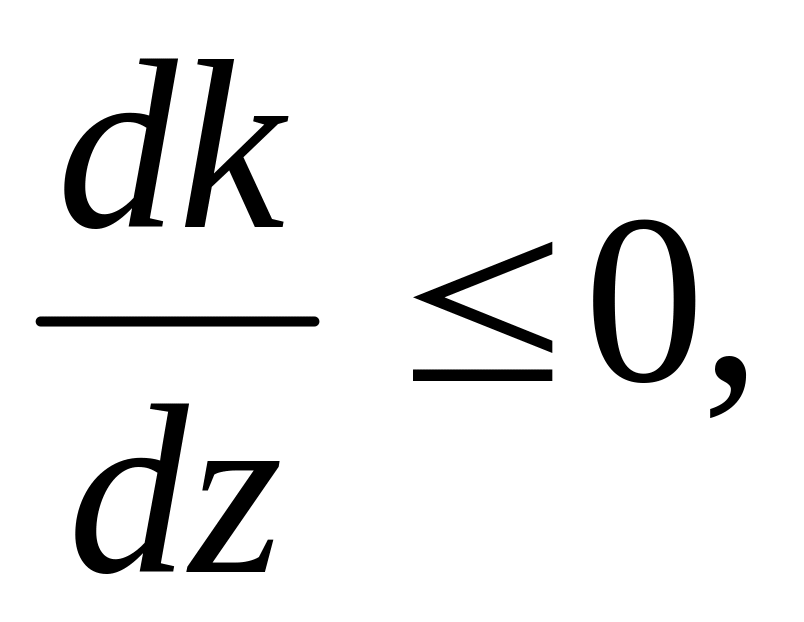то k спадає при збільшенні z..

Таким чином, якщо

(19)

то й при збільшенні z лінія рівня повертається проти годинникової стрілки.

Якщо

(20)

то й збільшенні z лінія рівня повертається за годинниковою стрілкою.

З рівняння (15) випливає, що при тобто при лінія рівня проходить через початок координат і, отже, поворот здійснюється навколо початку координат.

Якщо, й/або , то рівняння (15) визначає пучок прямих, які проходять через деяку точку Рівняння пучка прямих, які проходять через задану точку з урахуванням (15), запишеться у вигляді:

(21)

Так як з (15) маємо

(22)

То підставивши (21) в (20), одержимо

(23)

звідки

(24)

Останнє рівняння повинне виконуватися для всіх значень z. Це можливо, тільки якщо

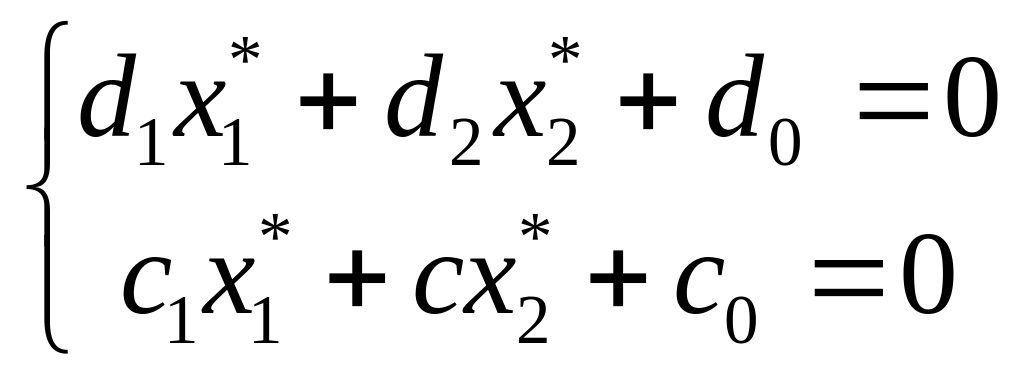(25)

Таким чином, у випадку якщо й/або , поворот лінії рівня здійснюється навколо точки з координатами , які є розв’язком системи (25).

Установивши напрям повороту, знаходимо вершину або вершини багатокутника розв’язків, у яких функція приймає екстремальне значення, або встановлюємол необмеженість значення цільової функції задачі.