1. Задачі з сідловою точкою. Задачі в чистих стратегіях.

Розглянемо парну гру:

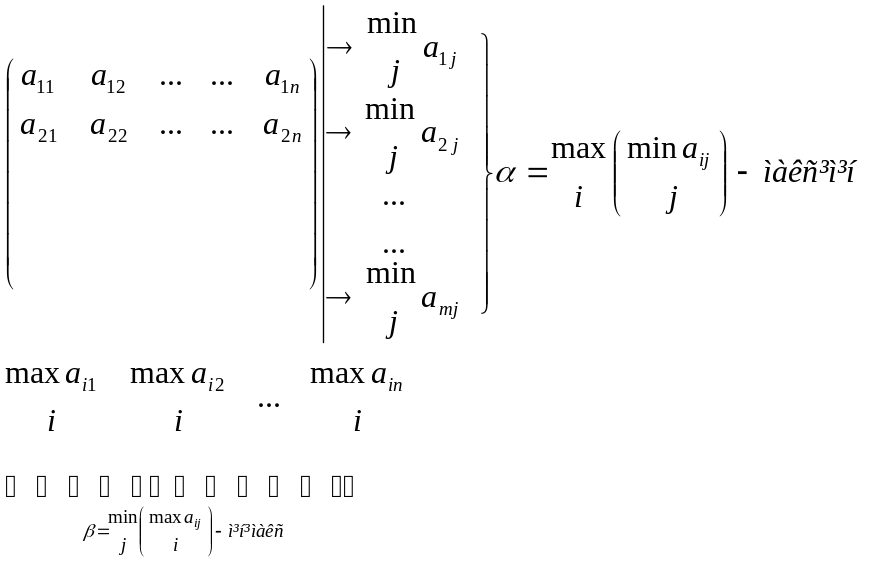
Приклад 1.Задана платіжна матриця А парної гри з нульовою сумою: А= . Знайти ціну гри, сідлову точку гри.

Приклад 2. .Задана платіжна матриця А парної гри з нульовою сумою: А= . Знайти верхнью та нижню ціну гри.

2. Ігри в мішаних стратегіях. Основна теорема теорії ігор.

Якщо немає сідловок точки, то гра ведеться в мішаних стратегіях, тобто розглядається не вибір можливої стратегії, а ймовірність з котрою обирається ця стратегія. Мішана стратегія визначається сукупністю ймовірностей різних стратегій.

Нехай гравець А для визначення своєї мішаної стратегії використав метод випадкового вибіру.

Нехай х₁ – ймовірність вибору 1-ої стратегії;

х₂ - ймовірність вибору 2-ої стратегії;

…………………………………………………

x_m - ймовірність вибору m-ої стратегії.

Означення 1. Мішаною стратегією гравця А називається упорядкований набір m чисел х₁, х₂, ….., x_m, які задовольняють умовам: 0≤x_i≤1, i= =1.

Мішані стратегії гравців А та В позначають =(x₁,x₂, …, x_m), =(y₁,y₂,…,y_n).

Всяка матрична гра з нульовою сумою має оптимальне рішення в мішаних стратегіях, при цьому відхилятися гравцям від цих стратегій не вигідно.

Теорема. О методі знаходження рішення.

Для того, щоб число ν було ціною гри, а Х^* та Y^* - оптимальними стратегіями, необхідно та достатньо, щоб виконувались умови:

j=

i=

Визначення оптимальних стратегій та ціни гри створюють процес знаходження рішення гри.

Теорема 2. Якщо один з гравців використовує мішану оптимальну стратегію, то його виграш дорівнює ціні гри ν незалежно від того, з якими частотами буде використовувати другий гравець стратегії, які вийшли до оптимальної стратегії( в тому числі і чисті стратегії).

Розглянемо гру з платіжною матрицею 2х2: A= .

Якщо сідлової точки нема, рішення гри є мішані стратегії =(х₁,х₂) та =(y₁,y₂) стратегії гравців А та В, для котрих ймовірністі x_i y_i відмінні від нуля, звуться активними.

Стратегію гравця А шукаємо по формулі ХА= , де Х=(х₁,х₂), =( ν, ν).

До даної системи рівнянь додаємо норміровочне рівняння х₁+х₂=1.

Для гравця В:

де Y= , = .

Розв’язавши систему рівнянь знайдемо оптимальні стратегії гравців та ціну гри ν.

Наслідок. Для того, щоб х^*, була оптимальною мішаною стратегією матричнох гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:

j=

Аналогічно для гравця В: Для того, щоб у^* була оптимальною мішаною стратегією матричної гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:

i=

Таким чином, для розв’язування гри необхідно визначити стратегії, що задовольняють вишенаведані системи обмежень та умови нормування:

0, =1, i= , , =1, j= .

Цей наслідок дозволяє сформулювати для розв’язання гри пару задач лінійного програмування.

3. Зведення задач теорії ігор до задач лп.

Якщо один з гравців застосовує свою оптимальну стратегію х^*, то інший не може покращити своє становище, тобто для оптимальної стратегії справедливі співвідношення:

j= , x_i≥0, =1, i= за умов ν→Мах.

Перетворимо цю задачу, здійснивши підстановку p_i= , і отримаємо

→Min,тому що ν→Мах.

Таким чином, маємо задачу ЛП, розв’язуючи яку, отримаємо значення p_i, за допомогою яких шляхом оберної підстановки визначимо оптимальні значення ймовірностей, що складають оптимальну мішану стратегію.

А здійснивши підстановку q_j= і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:

.

Таким чином, процедура розв’язування гри двох осіб є наступною:

1. Розраховуємо нижню та верхню ціну гри; якщо вони рівні між собою, то гра розв’язана.

2. Спрощуємо гру шляхом виключення домінованих стратегій.

3. Формулюємо пару задач ЛП, розв’язавши одну з яких, встановлюємо оптимальну мішану стратегію одного з гравців (зручніше гравця В).

4. За розв’язком прямої задачі знаходимо розвязок двоїстої задачі.

5. Шляхом оберненої підстановки визначемо оптимальні стратегії для спрощеної гри та доповнюємо їх домінованими чистими стратегіями з ймовірністю використання, що рівні нулю.