- •Тема 1. Концептуальні аспекти математичного моделювання економіки.
- •Тема 2. Оптимізаційні економіко-математичні моделі.
- •Тема лекції: Математичне моделювання. Економічна та математична постановка матричних та оптимізаційних задач
- •Предмет математичного моделювання.
- •Класификація економіко – математичних моделей. Формальна класіфикація моделей.
- •Задачі математичного програмування.
- •4. Класифікація методів математичного програмування.
- •5. Задачі планування та організації виробництва.
- •5.1. Задача про максимальну рентабельність підприємства.
- •5.2. Задача про завантаження обладнання
- •6. Модель міжгалузевого балансу „Витрати - випуск”.
- •Коефіціети прямих та побічних витрат.
- •Питання для самоконтролю.
- •Тема 2.Загальна задача лінійного програмування та деякі зметодів її розв’язування
- •Тема лекції: Основні теореми та властивості задач лінійного програмування (лп).
- •1. Загальна форма задачі лінійного програмування (лп).
- •2. Основні теореми та властивості задачі лп.
- •3. Графічний метод розв’язання задач мп.
- •Алгоритм знаходження розв’язку задачі мп графічним методом.
- •Питання для самоконтролю.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач.
- •Тема лекції: Вирішення задач лп симплекс-методом. Двоїста задача лп.
- •1. Представлення задач лп в матричній та векторній формі.
- •2. Симплексний метод розв’язання задач лп. Теоретичні основи симплекс-метода.
- •3. Метод штучної бази.
- •4. Двоїста задача лп.
- •Двоїста задача
- •Питання для самоконтролю.
- •Тема 3. Задача лінійного програмування та методи її розв’язування.
- •Тема лекції: Транспортна задача
- •1 Економічна та математична моделі транспортної задачі.
- •2 Основні теореми транспортної задачі.
- •3. Метод північно-західного кута (діагональний.)
- •5. Метод потенціалів.
- •Питання для самоконтролю.
- •Тема 5. Цілочислове програмування
- •Тема 6.Нелінійні оптимізаційні моделі економічних систем
- •Тема лекції: Узагальнення задачі лінійного програмування.
- •Задачі цілочислового програмування.
- •2. Метод Гоморі.
- •3. Параметричне лінійне програмування.
- •Питання для самоконтролю.
- •Тема 7. Аналіз та управління ризиком в економіці.
- •Тема лекції: Економічний ризик: ігрові моделі. Матричні ігри
- •1. Постановка задач теорії ігор з нульовою сумою.
- •Задачі з сідловою точкою. Задачі в чистих стратегіях.
- •Ігри в мішаних стратегіях. Основна теорема теорії ігор.
- •Зведення задач теорії ігор до задач лп.
- •Питання для самоконтролю.
- •Тема 7. Нелінійні оптимізаційні моделі економічних систем
- •Тема лекції: Задача дробово-лінійного програмування
- •Постановка задачі дробово-лінійного програмування.
- •2. Приведення задачі дробово-лінійного програмування до задачі лінійного програмування.
- •3. Розв’янання задач дробово-лінійного програмування.
- •4. Графічне розв’язання задачі дробово-лінійного програмування.
- •Питання для самоконтролю.
- •Тема 6. Нелінійні оптимізаційні моделі економічних систем Лекція 8 Тема лекції: Задачі нелінійного програмування
- •1. Постановка задачі пошуку екстремуму функції.
- •2. Властивості опуклих множин і опуклих функцій
- •Необхідні та достатні умови безумовного екстремуму функції. Необхідні умови першого порядку
- •Необхідні умови екстремуму функції другого порядку
- •Достатні умови екстремуму
- •Перевірка виконання умов функції на екстремум.
- •Критерій Сильвестра перевірки достатніх умов екстремуму.
- •Умовний екстремум при обмеженнях типу рівність.
- •Стратегія вирішення задачі
- •Необхідні умови екстремуму першого порядку при обмеженнях типу рівність.
- •Питання для самоконтролю.
- •Тема 8. Система показників кількісного оцінювання ступеня ризику
- •Тема лекції: Економічний ризик
- •1. Поняття ризику. Причини виникнення, класифікація ризику.
- •3. Кількісні методи оцінки ризиків
- •4. Статистичні ігри
- •Питання для самоконтролю.
2. Метод Гоморі.
Сутність методу Гоморі (метод відтинання) полягає у тому, що спочатку розв’язується звичайна задача ЛП без урахування вимог цілочисельності змінних. Якщо отриманий оптимальний план задачі цілочисловий, то задача розв’язана. У протилежному випадку у модель вводиться спеціальне додаткове обмеження, що враховує цілочисельність змінних і володіє такими властивостями:
- вона повинна бути лінійною;
- вона повинна відтинати знайдений оптимальний нецілочисловий план задачі;
- не повинна відтинати ні одного цілочислового плану.
Додаткове обмеження, що має перелічені вище властивості, називається правильним відтинанням.
Це додаткове обмеження вводиться до оптимального плану якщо серед компонент оптимального є число з дробовую частиною. На базі цієї змінної будується додаткове обмеження Р.Гоморі:
![]()
де
![]() - дробова частина числа,
- дробова частина числа,
![]() =а-[a].
=а-[a].
[a] – ціла частина числа а, т.б. найбільше ціле число, яке не перевищує числа а.
Якщо оптимальний план задачі має де кілька дробових значень, то додаткову нерівність складають для тієї змінної яка має найбільшу дробову частину.
Геометричний зміст кожного лінійного додаткового обмеження відповідає проведенню прямої (гіперплощини), яка відтинає від многокутника допустимих розв’язків деяку його частину разом із оптимальним нечисловим планом. Причому не відтинаються точки з цілими координатами цієї області допустимих розв’язків. У результаті область допустимих розв’язків послабленої задачі поступово зменшується доти, доки всі змінні оптимального плану не набувають цілочислових значень.
Розглянемо метод Гоморі на прикладі.
Приклад 1.
![]()
за умов
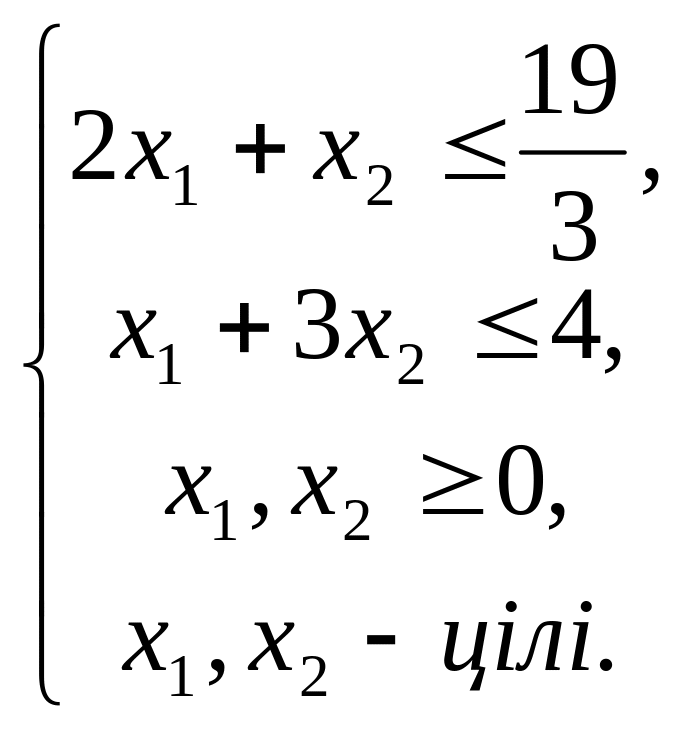
3. Параметричне лінійне програмування.
Параметричне програмування являє собою один з розділів математичного програмування, вивчає завдання, в яких цільова функція або обмеження залежать від одного або кількох параметрів. Необхідність розгляду подібних завдань обумовлена різними причинами. Однією з основних є та, що вихідні дані для чисельного рішення будь-якої реальної задачі оптимізації в більшості випадків визначаються наближено або може змінюватися під впливом якихось чинників, що може істотно позначитися на оптимальності вибираної програми (плану) дій. Відповідно, розумно вказувати не конкретні дані, а діапазон можливої зміни даних, що б в результаті рішення мати найкращі плани для будь-якого варіанту вихідних даних. З математичної точки зору параметричне програмування виступає як один із засобів аналізу чутливості рішення до варіації вихідних даних, оцінки стійкості рішення.
Зауважимо, що існують різні підходи до подібного аналізу (наприклад, на основі постановки двоїстої задачі). Тут ми, не посилаючись на двоїсті оцінки, розглянемо найпростіші варіанти рішення для самих найпростіших параметричних задач. Розглянемо задачу параметричного лінійного програмування, в якій тільки коефіцієнти цільової функції лінійно залежать від деякого єдиного параметра λ (часу, температури і т. п.): Відшукати максимум (або мінімум) функції:
![]()
за умов
![]()
![]()
Якщо
звернутися
до
геометричної
інтерпретації
задачі,
то можна
помітити,
що
вектор-градієнт
лінійної
форми
визначається
її
параметром.
Наприклад,
для цільової
функції
L
(х,
λ)
= λх1
+
(1-λ)
х2
при
різних
значеннях
параметра
λ
градієнт
визначає
різні
напрямки
зростання
функції.
Неважко
бачити,
що,
якщо
при
деякому
значенні
параметра
максимум
досягається
в
вершині
A,
то невелика
варіація
цього
значення
дещо
змінить
напрямок
градієнта,
але
не
змінить
положення
точки
максимуму.
Звідси
напрошується
висновок,
що
деякий
план,
оптимальний при
λ
=
λ0
оптимальний
і
в
околиці
λ0,
тобто при
α
≤ λ ≤ β
де
λ0![]() [α,
β].
Можна
помітити,
що
при
градієнті,
що став перпендикулярним
деякої
сторони
багатокутника
планів,
маємо
два
різних
оптимальних
опорних
плани
з
одним
і
тим
же
значенням
лінійної
форми,
звідки
можна
стверджувати
безперервність
екстремуму
лінійної
форми
за
λ.
[α,
β].
Можна
помітити,
що
при
градієнті,
що став перпендикулярним
деякої
сторони
багатокутника
планів,
маємо
два
різних
оптимальних
опорних
плани
з
одним
і
тим
же
значенням
лінійної
форми,
звідки
можна
стверджувати
безперервність
екстремуму
лінійної
форми
за
λ.
У разі
необмеженість
безлічі
планів
можна
стверджувати,
що
якщо
лінійна
форма
не
обмежена
при
λ
=
λ0,
то вона
не
обмежена
при
всіх
λ,
більших або менших
λ0.
Алгоритм
для
вирішення
завдань
параметричного
лінійного
програмування
в
разі
залежності
від
параметра
коефіцієнтів
цільової
функції
незначно
відрізняється
від
звичайного
симплексного
методу.
У
разі
залежності
від
параметра
компонент
вектора
правих
частин
обмежень,
тобто
рішення
задачі
пошуку
екстремуму
функції
![]()
за умов
![]()
Приклад 2.
![]()
за умов
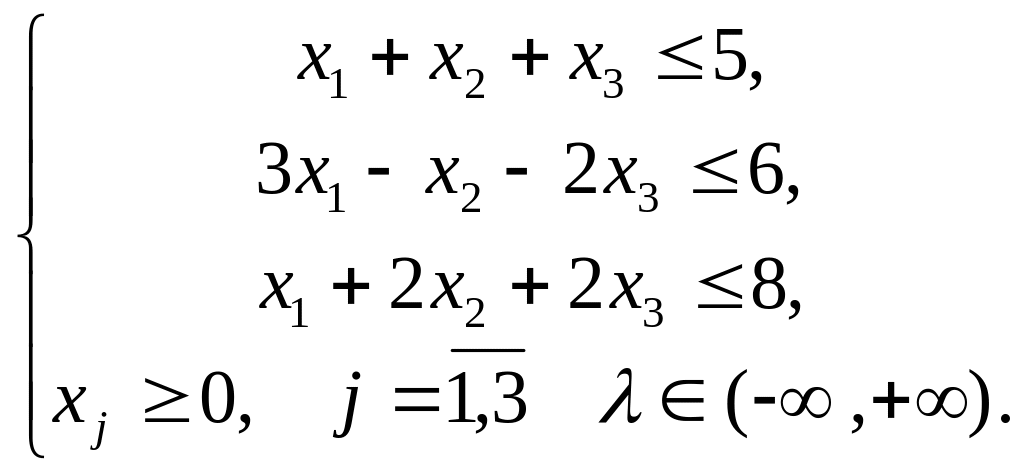
Приклад 3.
![]()
за умов

Для того щоб вирішити задачу, достатньо вирішити двоїсту задачу до неї, яка має вигляд
![]()
за умов