3.2.1 Математическая постановка задачи
Пусть наблюдается система функций
,
где
k – номер ряда. k = 1 .. s.
s – число временных рядов.
N – длина временного ряда.
i – номер отсчета.
Рядом в данном случае является
спектрограмма вибросигнала, снятая в
определенной точке. Требуется разложить
в ряд сумму компонент, интерпретировать
каждую и построить продолжение ряда
по
выбранным компонентам.
3.2.2 Алгоритм ssa
В результате применения метода ряд раскладывается на простые компоненты: тренды, сезонные, периодические и колебательные составляющие, а также шумовые компоненты. Полученное разложение может служить как для прогноза ряда в целом, так и отдельных его компонент.
Алгоритм состоит из трех этапов:
Построение матрицы наблюдений.
Анализ главных компонент.
Прогноз.
Для упрощения рассмотрим одномерный
временной ряд
.
Выберем n такое, что 0 < n < N - 1
– время жизни гусеницы. Пусть
–
длина гусеницы. Построим последовательность
Z из n векторов в пространстве
следующего
вида:
Будем называть Z нецентрированной матрицей наблюдений. В случае многомерного ряда матрицей наблюдений называется столбец из матриц наблюдений, соответствующий каждой из компонент.
Рассмотрим ковариационную матрицу полученной выборки:
Выполним ее сингулярное разложение (SVD):
V – ортогональная матрица собственных векторов:
Далее рассмотрим систему главных компонент:
После проведения анализа, следует восстановить матрицу наблюдений по главным компонентам:
Далее восстанавливаются исходные последовательности:
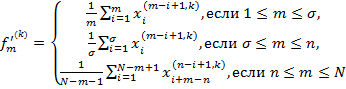
Затем начинается прогнозирование.
Числовой ряд
называется
продолжением ряда
,
если порождаемая им при гусеничной
обработке выборка лежит в той же
гиперплоскости, что и у исходного ряда.
Ранее был вычислен набор главных
компонент
.
Определим:
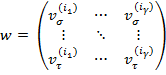
Также определим:
Тогда прогнозируемое значение в точке N + 1 вычисляется по формуле [13]:
Пример прогнозирования трех одномерных временных рядов приведен на рисунке 2 [14].
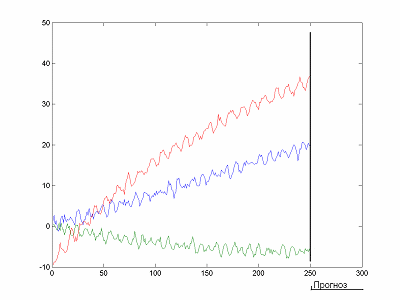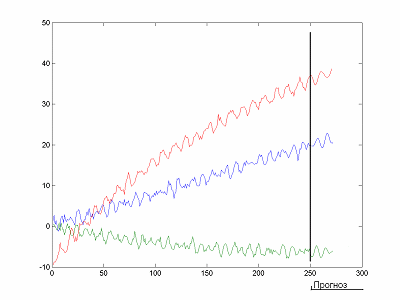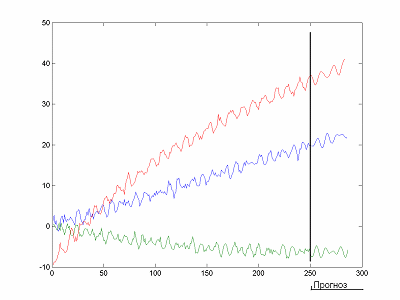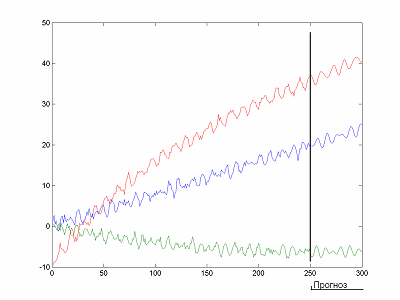
Риcунок 2 – Построение прогноза методом SSA (Анимация: 6 кадров, количество циклов воспроизведения не ограничено, 10 килобайт)
3.3 Обзор методов планирования ремонтных работ
Способы планирования мер по техническому обслуживанию и ремонту классифицируются следующим образом:
По событию — например, устранение поломки оборудования, используется если себестоимость ремонта относительно низкая, а брак продукции, который получается в результате поломки оборудования, невысок и не повлияет на выполнение обязательств перед заказчиками.
Регламентное обслуживание — для оборудования, с предусмотренными режимами и регламентами обслуживания, изначально предполагающего регулярное применение соответствующих мер по поддержанию работоспособности, такой вид обслуживания дает самый высокий процент готовности оборудования, но он и самый дорогой, поскольку реальное состояние оборудования может и не требовать ремонта.
По состоянию — экспертным путем или с помощью измерителей, установленных на оборудовании, проводится оценка состояния оборудования, и на основании этой оценки делается прогноз, когда это оборудование надо выводить в ремонт. Плюсы этого вида обслуживания: его себестоимость меньше, а готовность оборудования к выполнению производственных программ достаточно высока.
Все методы календарного планирования можно разделить на несколько групп:
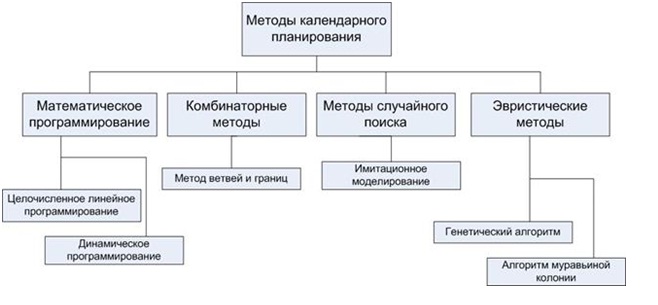
Рисунок 3 – Методы календарного планирования
Анализ приведенных методов показал, что сложность использования как комбинаторного метода, так и метода динамического программирования связана с экспоненциальным ростом длительности вычислений от размерности задачи. К тому же в задачах календарного планирования на каждом шаге планирования изменяется система ограничений, что затрудняет применение симплекс-метода, как части метода ветвей и границ. Для использования имитационного моделирования необходим большой объем статистических данных, доступ к которым на предприятии обычно затруднен. Таким образом, наиболее перспективным будет выбор эвристических методов. В настоящий момент разработано множество эвристических методов, основанных на применении генетических алгоритмов и их модификаций, позволяющих находить близкое к оптимальному решение задачи календарного планирования с ограниченными ресурсами [15].