Питання для самоперевірки

1. Що таке вектор?

2. Як знайти довжину вектора, якщо відомі його координати?

3. Які вектори називаються колінеарними?

4. Який добуток векторів і називається скалярним?

5. Як знайти кут між векторами, заданими в координатній формі?

6. Який добуток векторів і називається векторним?

7. Як обчислюється векторний добуток у координатній формі?

8. Дати означення мішаного добутку трьох векторів.

9. Які вектори називаються компланарними?

Завдання для самостійної роботи

1. При яких значеннях і вектори й колінеарні?

2. Знайти скалярний добуток векторів і .

3. Знайти косинус кута між векторами , .

4. Знайти площу паралелограма, побудованого на векторах , .

5. Знайти площу трикутника з вершинами , , .

6. Чи є компланарними вектори , , ?

7. Задано вершини піраміди , , , . Обчислити її об’єм і довжину висоти, опущеної на грань .

Практичне заняття № 4 з теми “ Пряма на площині. Площина в просторі. Різні види рівняння площини. Кут між двома площинами. Умови їх паралельності і перпендикулярності. Пряма в просторі. Різні види рівняння прямої в просторі. Кут між двома прямими. Пряма і площина в просторі. Кут між прямою і площиною. Відстань від точки до площини. Різні види рівняння прямої на площині. Кут між двома прямими”

1. Пряма на площині. Різні види рівняння прямої на площині. Кут між двома прямими.

Основними рівняннями прямої на площині є

1. Загальне рівняння – Ax + By + C = 0, (4.1) Ненульовий вектор , який перпендикулярний до даної прямої, називається нормальним вектором прямої.

2. Рівняння прямої з кутовим коефіцієнтом має вигляд

, (4.2)

де – кутовий коефіцієнт прямої, тобто тангенс кута, який пряма утворить з додатним напрямом осі 0х, причому цей кут відраховується від осі 0х до прямої проти годинникової стрілки, – величина відрізка, що відтинається прямою на осі ординат (рис. 4.1).

– кутовий коефіцієнт прямої, що проходить через точки і .

3 . Рівняння прямої, що проходить через дві задані точки , визначається за формулою . (4.3)

4. Рівняння прямої у відрізках на осях має вигляд

, (4.4) де а - величина відрізка, що відтинається прямою від осі 0х, а - величина відрізка, що відтинається прямою від осі 0у. Кожний із відрізків відкладений з початку координат (рис. 4.2).

5. Канонічне рівняння прямої – . (4.5)

У цьому рівнянні – точка, яка належить даній прямій; m, n – координати напрямного вектора .

Напрямним вектором прямої називають ненульовий вектор, паралельний цій прямій.

Кутом між прямими а і b називають кут, на який треба повернути першу пряму а навколо точки перетину цих прямих проти руху годинникової стрілки до співпадання її з другою прямою b.

Якщо дві прямі задані рівняннями з кутовими коефіцієнтами , , то кут між ними  визначають за формулою

. (4.6)

Якщо прямі задано загальними рівняннями , , або канонічними рівняннями , , то , ,

. (4.7)

Умова паралельності двох прямих:

а) Якщо прямі задано рівняннями з кутовими коефіцієнтами, то необхідна і достатня умова їх паралельності: .

б) Для випадку, коли прямі задано загальними рівняннями, необхідна і достатня умова їх паралельності визначається умовою: .

Умова перпендикулярності двох прямих:

а) У випадку, коли прямі задано рівняннями з кутовими коефіцієнтами, то необхідна і достатня умова їх перпендикулярності полягає в тому, що їх кутові коефіцієнти обернені за величиною і протилежні за знаком, тобто або .

б) Якщо прямі задано загальними рівняннями, то умова їх перпендикулярності полягає у виконанні рівності .

Відстань d від точки до прямої обчислюється за формулою

(4.8)

2. Пряма і площина у просторі. Різні види рівняння площини. Кут між двома площинами. Умови їх паралельності і перпендикулярності. Відстань від точки до площини. Кут між прямою і площиною

Загальне рівняння площини має вигляд – . (4.9)

Косинус кута між двома площинами і визначають за формулою:

(4.10)

Умова перпендикулярності двох площин має вигляд:

Умова паралельності двох площин має вигляд:

Відстань від точки N( ) до площини визначають за формулою:

. (4.11)

Рівняння площини, що проходить через три дані точки , , , має вигляд:

. (4.12)

Канонічне рівняння прямої в просторі:

(4.13)

де – координати точки, через яку проходить пряма, а m, n, p – координати напрямного вектора прямої.

Загальне рівняння прямої в просторі:

(4.14)

,

Рівняння прямої, що проходить через дві задані точки і , має вигляд :

(4.15)

Косинус кута між двома прямими і визначають за формулою:

. (4.16)

Умова перпендикулярності двох прямих у просторі має вигляд: (4.17)

Умова паралельності двох прямих у просторі має вигляд:

(4.18)

Гострий кут між прямою та площиною визначають як кут між прямою та проекцією цієї прямої на площину.

Синус цього кута визначають за формулою:

(4.19)

Умова паралельності прямої та площини у просторі має вигляд:

(4.20)

Умова перпендикулярності прямої та площини у просторі має вигляд:

(4.21)

Приклад 4.1. Дано вершини трикутника АВС: А(0, 1), В(6, 5), С(12, –1). Знайти: а) рівняння сторони АВ; б) рівняння висоти СН; в) рівняння медіани АМ; г) точку N перетину медіани АМ і висоти СН; д) рівняння прямої, що проходить через вершину С паралельно стороні АВ; є) відстань від точки С до прямої AB.

Розв'язок. а) Знайдемо рівняння сторони АВ як прямої, що проходить через дві задані точки А(0,1) і В(6, 5).

4х = 6у – 6, 4х – 6у + 6 = 0, 2х – 3у + 3 = 0 – рівняння АВ.

б) Знайдемо кутовий коефіцієнт сторони АВ. Для цього приведемо рівняння АВ до вигляду рівняння з кутовим коефіцієнтом

3у = 2х + 3 ,

У силу умови перпендикулярності кутовий коефіцієнт висоти, що проведена з вершини С, дорівнює . Рівняння цієї висоти має вигляд

в) Точка М поділяє сторону ВС навпіл, тому координати точки М знаходимо за формулами:

, . . Отже, М (9, 2).

Складемо рівняння медіани АМ як прямої, що проходить через точки А(0, 1) і М(9, 2).

х – 9у + 9 = 0 – рівняння АМ.

г) Точку N перетину медіани АМ і висоти СН знайдемо, розв'язавши систему з рівнянь АМ і СН:

д) Складемо рівняння прямої, що проходить через вершину С паралельно стороні АВ.

2х – 3у + 3 = 0 – рівняння АВ

. У силу паралельності прямих кутовий коефіцієнт прямої, що проходить через С паралельно стороні АВ, теж дорівнює . Отже,

є) Обчислимо відстань від точки С до прямої АВ.

Приклад 4.2. Дано чотири точки , , , . Скласти рівняння: а) площини ; б) прямої ; в) прямої , перпендикулярної до площини ; г) прямої , паралельної прямій ; д) площини, що проходить через точку перпендикулярно до прямої . Обчислити: е) синус кута між прямою і площиною ; ж) косинус кута між координатною площиною 0ху і площиною .

Розв'язок. а) Складемо рівняння площини як площини, що проходить через три точки . Скористаємось формулою (4.12)

.

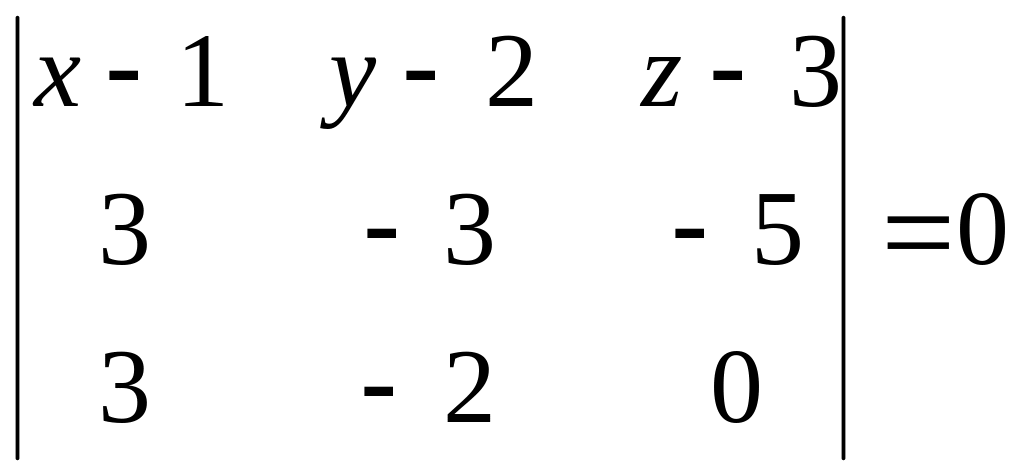Обчисливши визначник, отримаємо загальне рівняння площини в загальному вигляді:

б) Складемо рівняння прямої як прямої, що проходить через дві точки і , скориставшись формулою (4.15):

в) Запишемо рівняння пучка прямих, що проходять через точку :

.

Напрямний вектор прямої колінеарний нормальному вектору площини . Тому з умови колінеарності двох векторів можемо записати, що , а отже, рівняння прямої , що перпендикулярна до площини , має вигляд :

.

г) Запишемо рівняння пучка прямих, що проходять через точку :

.

З умови паралельності прямої випливає, що .

Тому рівняння прямої , що паралельна прямій , має вигляд:

д) Рівняння в'язки площин, що проходять через точку , має вигляд:

Звідси рівняння в'язки площин, що проходять через точку , буде мати вигляд:

Напрямний вектор прямої є нормальним вектором площини, а тому, скориставшись (4.21), можемо записати, що , або .

,

е) Синус кута між прямою і площиною обчислимо, використовуючи формулу для обчислення між прямою і площиною.

Складемо рівняння прямої :

Рівняння площини :

m = 1, n = –1, p = 3, A = –10, B = –15, C = 3.

ж) Рівняння координатної площини 0ху має вигляд: z = 0.

Обчислимо косинус кута між координатною площиною 0ху і площиною , використовуючи формулу для обчислення кута між двома площинами: