
- •Для квадратних матриць вводять поняття оберненої матриці.
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Пряма є вертикальною асимптотою кривої, якщо (тобто, точка є точкою розриву функції другого роду).
- •7.4 Схема дослідження властивостей та побудова графіка функції
- •1. Знайти область визначення функції.
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Питання до модульного контролю
- •Список літератури
- •39600, М. Кременчук, вул. Першотравнева, 20
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
КРЕМЕНЧУЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
ІМЕНІ МИХАЙЛА ОСТРОГРАДСЬКОГО

МЕТОДИЧНІ ВКАЗІВКИ
ЩОДО ПРАКТИЧНИХ ЗАНЯТЬ
З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ
“МАТЕМАТИЧНІ ОСНОВИ ІНФОРМАЦІЙНОЇ ДІЯЛЬНОСТІ”
ДЛЯ СТУДЕНТІВ I КУРСУ ДЕННОЇ ТА ЗАОЧНОЇ ФОРМ НАВЧАННЯ
З НАПРЯМУ 6.020105 – "ДОКУМЕНТОЗНАВСТВО ТА ІНФОРМАЦІЙНА ДІЯЛЬНОСТЬ "
КРЕМЕНЧУК 2012
Методичні вказівки щодо практичних занять з навчальної дисципліни “Математичні основи інформаційної діяльності” для студентів I курсу денної та заочної форм навчання з напряму 6.020105 – "Документознавство та інформаційна діяльність"
Укладачі доц. Скапа І.В.,
ст. викл. Набок Т.А.
Рецензент доцент, к.ф.–м.н., Семенов В.О
Кафедра інформатики і вищої математики
Затверджено методичною радою КрНУ імені Михайла Остроградського
Протокол № ____ від “____” _________ ____2012 року
Голова методичної ради _______________ проф. В.В. Костін
ЗМІСТ
Вступ……………………………………………………………………...........4
Практичне заняття № 1 з теми “Матриці. Лінійні операції над матрицями. Добуток матриць. Визначники 2-го і 3-го порядків та їх властивості. Мінори та алгебраїчні доповнення. Обернена матриця”……………………………………...5
Практичне заняття № 2 з теми “Розв’язування систем лінійних алгебраїчних рівнянь за формулами Крамера, матричним методом і методом Гаусса. Ранг матриці. Визначення рангу матриці. Теорема Кронекера-Капеллі. Метод Жордана-Гаусса для розв`язання систем лінійних рівнянь”…………….10
Практичне заняття № 3 з теми “ Скалярні і векторні величини. Лінійні операції над векторами. Кут між векторами. Скалярний добуток векторів і його властивості”……………………………………………………………………..….23
Практичне заняття № 4 з теми “ Пряма на площині. Площина в просторі. Різні види рівняння площини. Кут між двома площинами. Умови їх паралельності і перпендикулярності. Пряма в просторі. Різні види рівняння прямої в просторі. Кут між двома прямими. Пряма і площина в просторі. Кут між прямою і площиною. Відстань від точки до площини. Різні види рівняння прямої на площині. Кут між двома прямими”……………………………………30
Практичне заняття № 5 з теми “ Функція. Способи завдання функції. Класифікація основних елементарних функцій. Границя функції в точці та на нескінченності. 1-ша та 2-га визначні границі”…………………………………..40
Практичне заняття № 6 з теми “ Похідна функції, її геометричне і механічне тлумачення. Основні правила диференціювання. Таблиця похідних основних елементарних функцій. Диференціал функції”…………………….…48
Практичне заняття № 7 з теми “ Інтервали зростання і спадання функції. Екстремум функції. Інтервали опуклості графіка функції. Асимптоти. Дослідження функцій за допомогою похідних ”………………………………....53
Питання до модульного контролю………………………………................62
Список літератури……………………………………………………….......65
ВСТУП
Мета і завдання самостійної роботи: навчити студентів самостійно вивчати та працювати з навчальною та спеціальною літературою з розділів математичних основ інформаційної діяльності. Допомогти студентам ставити та вирішувати прикладні задачі, користуватися засобами комп'ютерної математики, самостійно здобувати необхідні для вирішення практичних завдань знання.
Види самостійної роботи: з підручниками, у електронної бібліотеці, з конспектом лекцій викладача, пошук необхідних матеріалів у мережі Internet.
Самостійна робота студентів забезпечується підручниками, навчальними та методичними посібниками, які є у бібліотеці КрНУ імені Михайла Остроградського. Також студент може користуватися конспектами лекцій та практичних занять викладача.
Методичні вказівки містять теми та погодинний розклад самостійної роботи, а також питання до модульного контролю. Кожна тема містить питання, що виносять на самостійне опрацювання; питання для самоперевірки; перелік літератури з вказівкою сторінок, де можна знайти відповіді на питання для самостійного опрацювання. Студент повинен знайти літературу, вивчити необхідні теми, а потім відповісти на питання для самоперевірки.
Займатися самостійно студент може у бібліотеці або вдома у вільний від навчання час. Також студент повинен звертатися за допомогою до викладачів під час консультацій, які проводяться на кафедрі згідно з графіком.
Практичне заняття № 1 з теми “Матриці. Лінійні операції над матрицями. Добуток матриць. Визначники 2-го і 3-го порядків та їх властивості. Мінори та алгебраїчні доповнення. Обернена матриця”
1.1 Визначення матриці
Матрицею
А
= (![]() )
розміру m
)
розміру m![]() n
називається
прямокутна таблиця чисел, складена з m
рядків
і
n стовпців:
n
називається
прямокутна таблиця чисел, складена з m
рядків
і
n стовпців:
 ;
;
![]() .
.
1.2 Лінійні операції над матрицями
Сумою
( різницею) двох матриць
![]() і
і
![]() є матриця
є матриця
![]() ,
для якої
,
для якої
![]() ,
і яка позначається
,
і яка позначається
![]() .
.
Добутком
матриці
![]() на
число
на
число
![]() називається матриця
називається матриця
![]() ,
для якої
,
для якої
![]() .
.
Матрицю А будемо називати узгодженою з матрицею В, якщо кількість стовпців матриці А дорівнює кількості рядків матриці В.
1.3 Множення матриць
Добутком
матриці
![]() розміру
m
розміру
m![]() r
на
матрицю
r
на
матрицю
![]() розміру r
n
називається матриця
розміру r
n
називається матриця
![]() розміру m
n
з
елементами
розміру m
n
з
елементами
![]() ,
кожний елемент якої дорівнює сумі
добутків відповідних елементів
,
кожний елемент якої дорівнює сумі
добутків відповідних елементів
![]() -го
рядка матриці
-го
рядка матриці
![]() на відповідні елементи
на відповідні елементи
![]() -го
стовпця матриці
-го
стовпця матриці
![]() :
:
![]() .
.
1.4 Визначники 2-го і 3-го порядків та їх властивості. Мінори та алгебраїчні доповнення.
Визначником квадратної матриці другого порядку є число, яке обчислюється за правилом:
![]() .
.
Визначником квадратної матриці третього порядку є число, що обчислюється за правилом

Мінором
![]() елемента
елемента
![]() матриці
матриці
![]() -го
порядку називають визначник
-го
порядку називають визначник
![]() порядку, який утворюється з даної матриці
внаслідок викреслювання рядка і стовпця,
на перетині яких розташований елемент
.
порядку, який утворюється з даної матриці
внаслідок викреслювання рядка і стовпця,
на перетині яких розташований елемент
.
Алгебраїчним
доповненням
![]() елемента
визначника
-го
порядку називають мінор цього елемента,
помножений на
елемента
визначника
-го
порядку називають мінор цього елемента,
помножений на
![]() .
.
![]() .
.
1.5 Обернена матриця
Для квадратних матриць вводять поняття оберненої матриці.
Якщо
для матриці
існує така матриця
![]() ,
що
,
що
![]() ,
де
,
де
![]() – одинична матриця, то матриця
називається оберненою
матрицею
до матриці
.
– одинична матриця, то матриця
називається оберненою
матрицею
до матриці
.
Невиродженою матрицею називається квадратна матриця, визначник якої не дорівнює нулю. У протилежному випадку матриця називається виродженою.
Для того, щоб дана матриця мала обернену, необхідно і достатньо, щоб вона була невиродженою.
Якщо матриця невироджена, то для неї існує обернена матриця
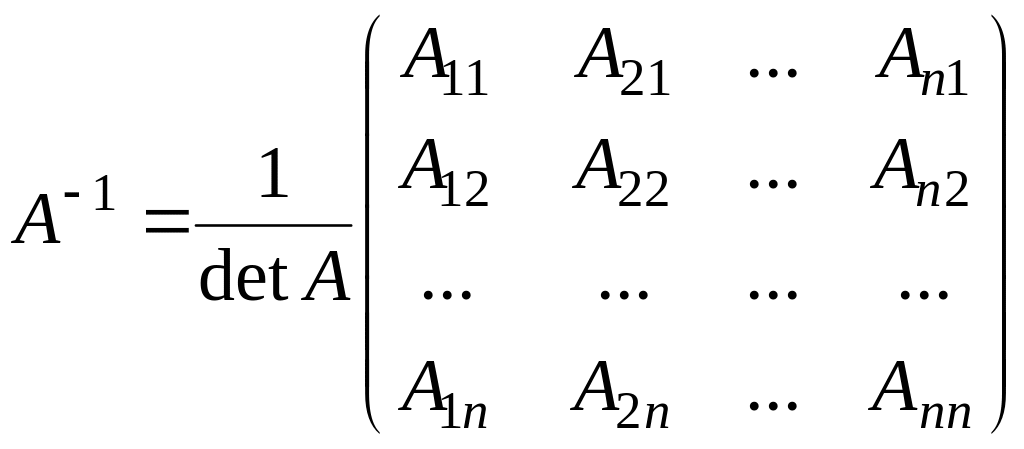 ,
,
де
–
алгебраїчне доповнення елемента
визначника матриці А,
а
![]() – її визначник.
– її визначник.
Приклад
1.1.
Дано
дві матриці
 Знайти: а)
Знайти: а)
![]() ;
б)
АВ.
;
б)
АВ.
Розв'язок.
а)
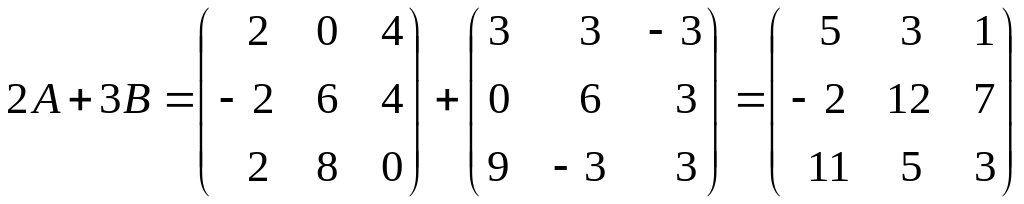 .
.
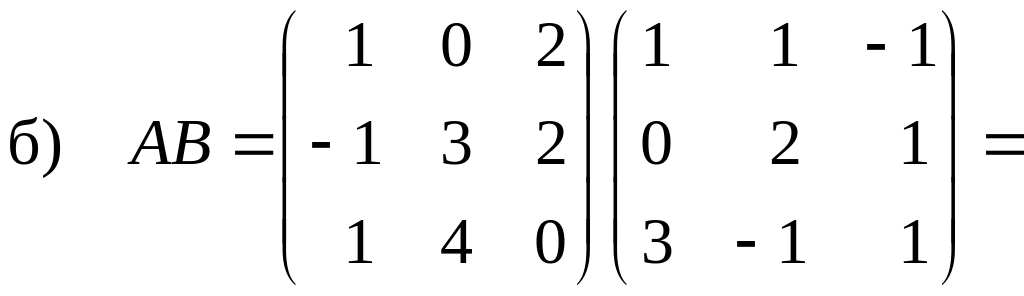
 Приклад
1.2.
Дано
дві матриці
Приклад
1.2.
Дано
дві матриці
 .
Знайти
.
Знайти
![]() та
та
![]() .
.
Розв'язок. Знайдемо :
 А
тепер знайдемо
.
А
тепер знайдемо
.

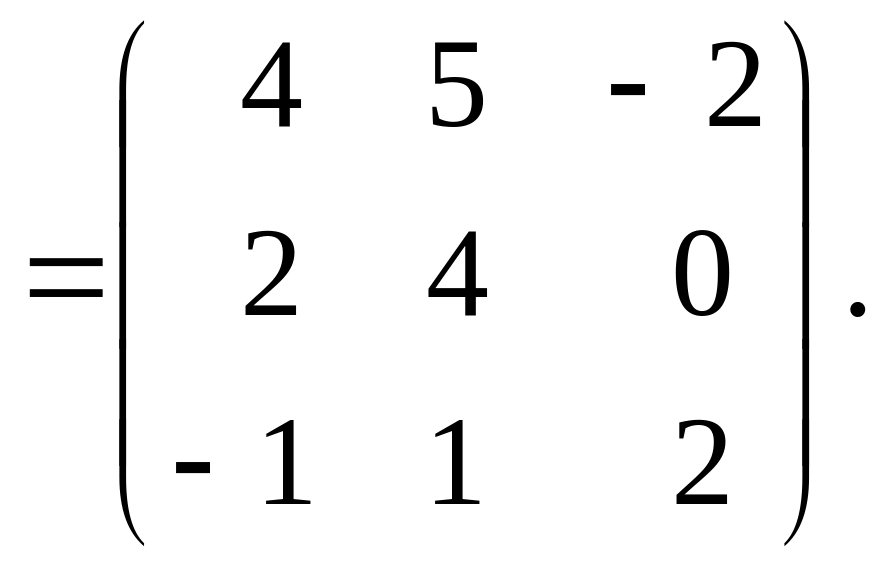
З
наведеного прикладу видно, що
![]() .
.
Приклад
1.3.
Дана
матриця
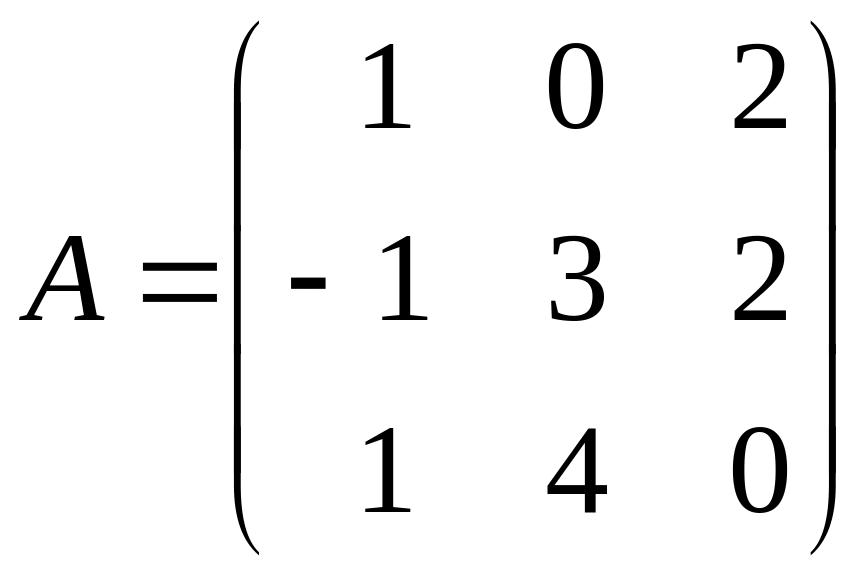 .
Знайти: а)
.
Знайти: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Розв'язок. а) Обчислимо визначник матриці А
 Тому що
Тому що
![]() ,
то обернена матриця існує
,
то обернена матриця існує
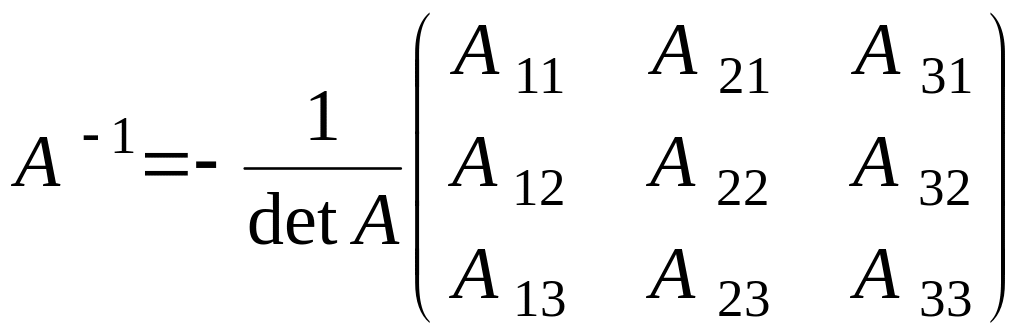 .
.
Знайдемо
алгебраїчні доповнення
![]() елементів матриці
:
елементів матриці
:
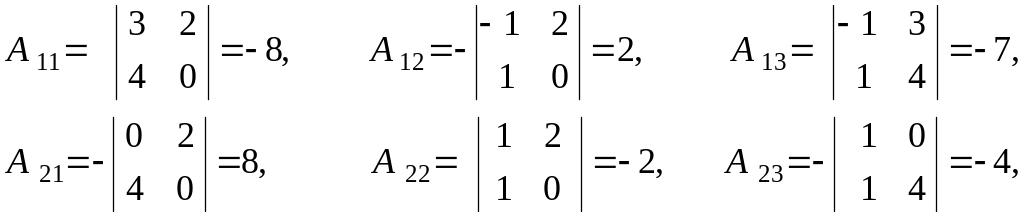
![]()
Отже,
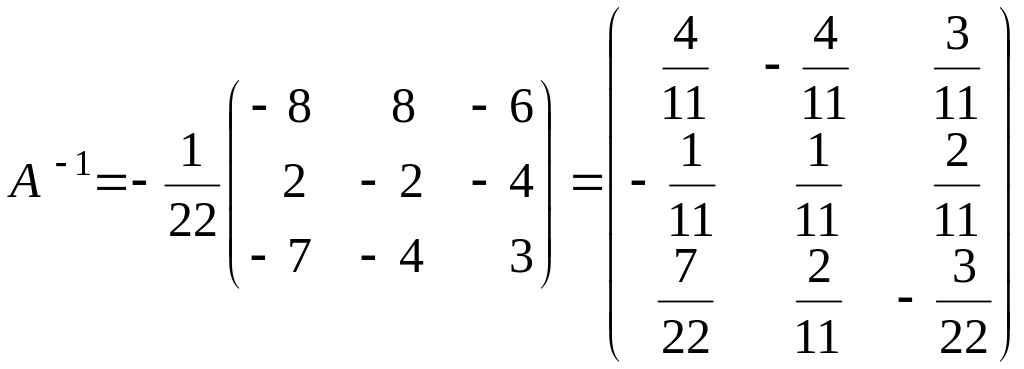 .
.![]()
б)


в)
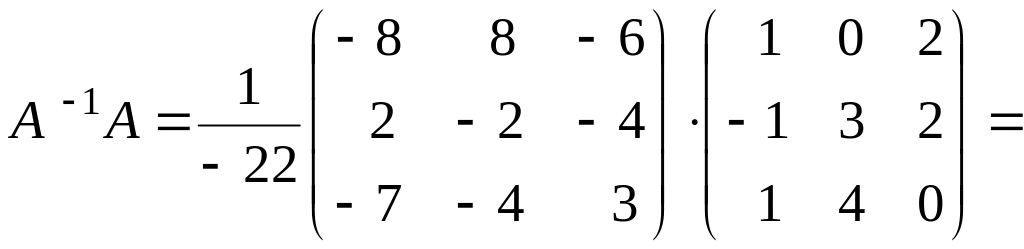

Питання для самоперевірки
1. Що називається матрицею?
2. Які матриці можна перемножувати?
3. Дайте визначення оберненої до даної матриці.
4. Що називається мінором елемента визначника -го порядку?
5. Що називається алгебраїчним доповненням елемента визначника -го порядку?
6. Назвіть основні властивості визначників.
Завдання для самостійної роботи
1.
Знайти матрицю
![]() ,
якщо
,
якщо
 .
.
2.
Яку матрицю
слід додати до матриці
 ,
щоб одержати одиничну матрицю?
,
щоб одержати одиничну матрицю?
3.
З'ясувати, чи є переставними матриці
![]() і
і
![]() ?
?
4. При
яких значеннях
![]() існує обернена матриця
,
якщо
існує обернена матриця
,
якщо
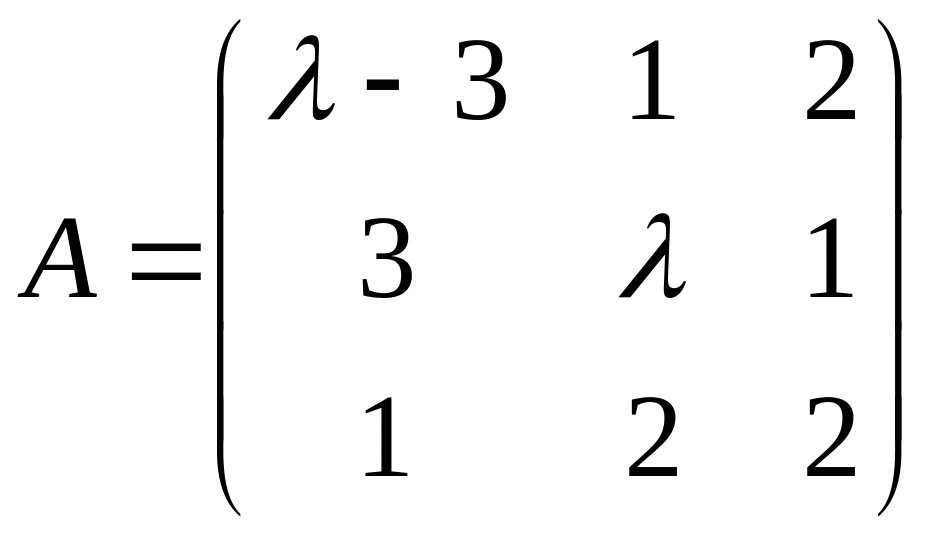 ?
?
5.
Дано
дві матриці
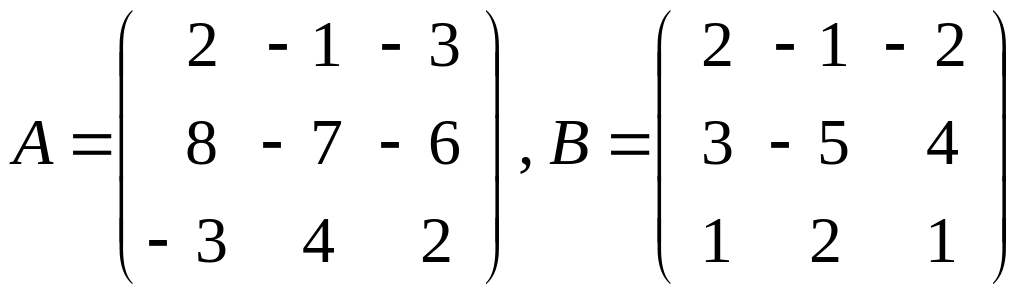 .
Знайти: а) АВ;
б)
.
Знайти: а) АВ;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Практичне заняття № 2 з теми “Розв’язування систем лінійних алгебраїчних рівнянь за формулами Крамера, матричним методом і методом Гаусса. Ранг матриці. Визначення рангу матриці. Теорема Кронекера-Капеллі. Метод Жордана-Гаусса для розв`язання систем лінійних рівнянь”
2.1 Основні поняття та визначення
Системою
m
лінійних
рівнянь
з n
невідомими
![]() називається система, що має вигляд
називається система, що має вигляд
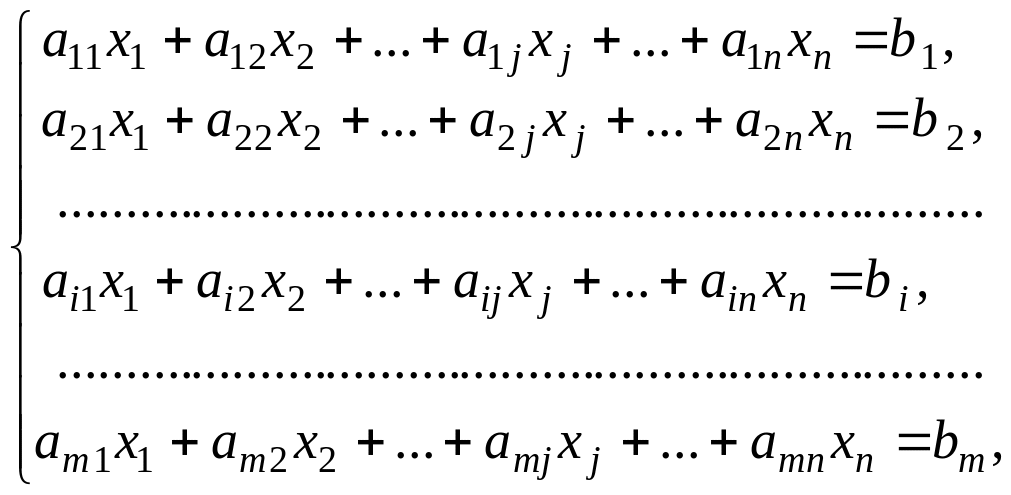 (2.1)
(2.1)
де
![]() –
дійсні числа, названі відповідно
коефіцієнтами
при невідомих і
вільними
членами
рівнянь.
–
дійсні числа, названі відповідно
коефіцієнтами
при невідомих і
вільними
членами
рівнянь.
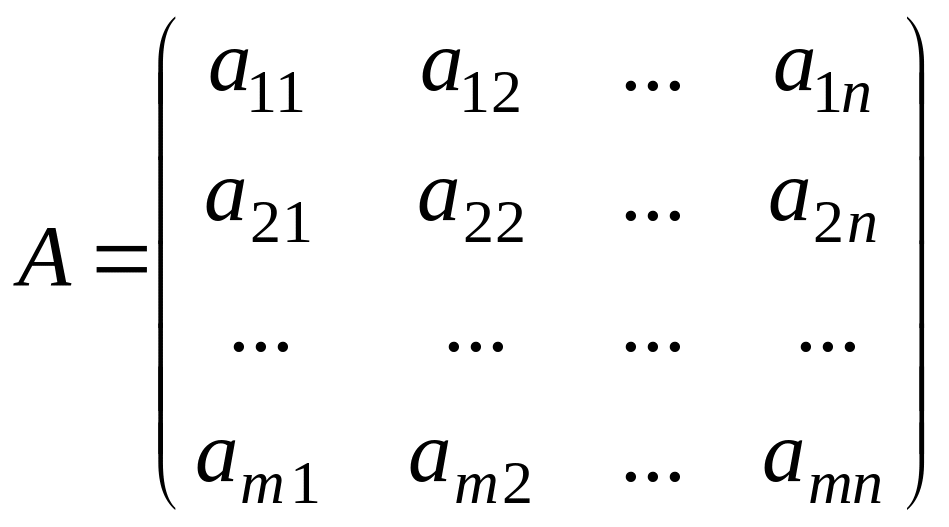 –
основна
матриця системи.
–
основна
матриця системи.
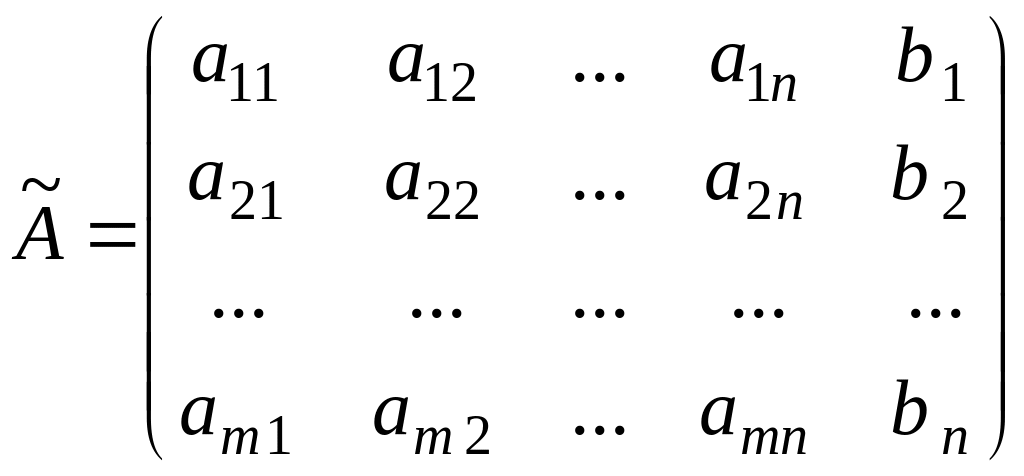 – розширена
матриця системи.
– розширена
матриця системи.
Впорядкована
система чисел
![]() називається розв'язком
системи
(2.1), якщо кожне з рівнянь (2.1) перетворюється
на тотожність після підстановки замість
називається розв'язком
системи
(2.1), якщо кожне з рівнянь (2.1) перетворюється
на тотожність після підстановки замість
![]() відповідно чисел
відповідно чисел
![]() .
.
Якщо в
правій частині системи (2.1) всі вільні
члени дорівнюють нулю, то система
називається однорідною,
якщо ж хоча б одне
![]() , то система називається неоднорідною.
, то система називається неоднорідною.
Система лінійних рівнянь називається сумісною, якщо вона має хоча б один розв'язок, і несумісною, якщо вона не має розв'язків.
Сумісна система лінійних рівнянь називається визначеною, якщо вона має єдиний розв'язок, і невизначеною, якщо вона має нескінченну множину розв'язків.
2.2 Розв’язування систем лінійних алгебраїчних рівнянь за формулами Крамера
Розглянемо систему (2.1) n лінійних рівнянь із n невідомими

де
– коефіцієнти системи;
![]() –
вільні члени. Визначник n-ого
порядку
–
вільні члени. Визначник n-ого
порядку
![]() ,
елементами якого є коефіцієнти при
невідомих, називається визначником
системи.
Якщо визначник системи
,
елементами якого є коефіцієнти при
невідомих, називається визначником
системи.
Якщо визначник системи
![]() ,
то єдиний розв'язок системи можна знайти
за формулами
Крамера:
,
то єдиний розв'язок системи можна знайти
за формулами
Крамера:
![]() (2.2)
(2.2)
де
![]() –
визначники n-ого
порядку, утворені із визначника системи
заміною 1, 2, …, n-ого
стовпців визначника
відповідно стовпцем вільних
–
визначники n-ого
порядку, утворені із визначника системи
заміною 1, 2, …, n-ого
стовпців визначника
відповідно стовпцем вільних
членів
![]() .
.
2.3 Розв’язування систем лінійних алгебраїчних рівнянь матричним методом
Скориставшись правилом добутку матриць, систему (2.1) можна записати у матричній формі: АХ = В, де

Якщо
визначник системи
![]() відмінний від нуля, то розв'язок системи
має вигляд
відмінний від нуля, то розв'язок системи
має вигляд
![]() .
.
2.4 Ранг матриці. Визначення рангу матриці
Якщо
матриця має відмінний від нуля мінор
порядку
![]() ,
а всі мінори вищого порядку (якщо вони
є) дорівнюють нулю, то число
називається рангом
матриці.
,
а всі мінори вищого порядку (якщо вони
є) дорівнюють нулю, то число
називається рангом
матриці.
Для квадратної матриці n-ого порядку rank А = n тоді й тільки тоді, коли матриця невироджена. Ранг нуль-матриці за означенням вважають рівним нулю.
Елементарні перетворення не змінюють рангу матриці.
Якщо
![]() ,
то будемо далі писати А
.
,
то будемо далі писати А
.
Будь-яку ненульову матрицю А за допомогою елементарних перетворень можна привести до вигляду
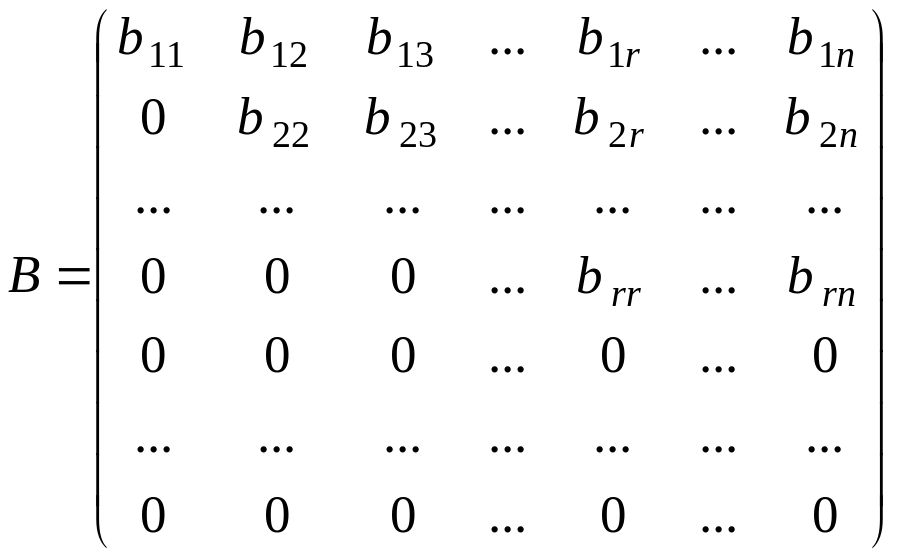 ,
,
де
![]() не дорівнюють нулю. Тоді
не дорівнюють нулю. Тоді
![]() ,
тому що наявність
,
тому що наявність
нульових рядків у матриці не впливає на її ранг.
Базисним мінором матриці називається всякий відмінний від нуля мінор, порядок якого дорівнює рангу даної матриці.
2.5 Теорема Кронекера – Капеллі
Система
лінійних рівнянь (2.1) сумісна тоді й
тільки тоді, коли ранг розширеної матриці
![]() дорівнює рангу матриці системи (
дорівнює рангу матриці системи (![]() ).
).
Якщо число невідомих дорівнює числу рівнянь, то система має єдиний розв'язок, коли
 .
.Якщо
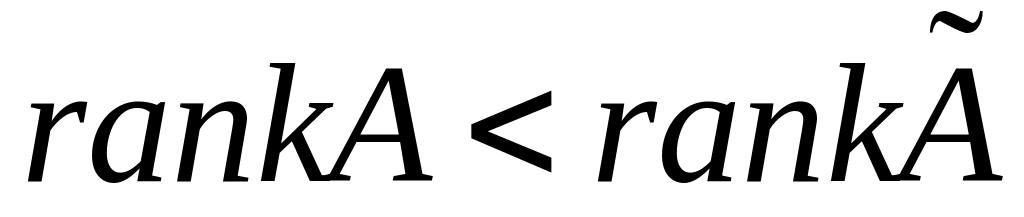 ,
то система розв'язків не має.
,
то система розв'язків не має.Якщо в системі (2.1) число рівнянь
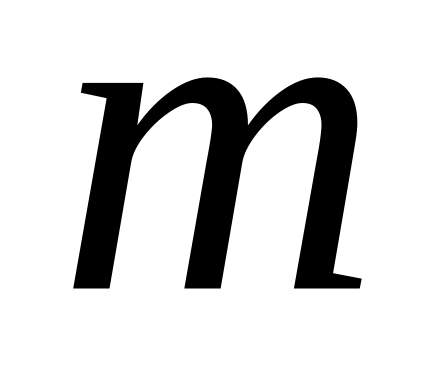 менше ніж число невідомих
(
менше ніж число невідомих
( )
і
)
і
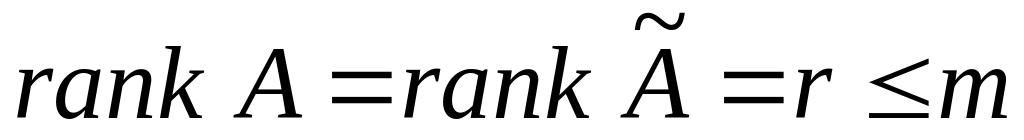 ,
то така система має нескінченну множину
розв'язків.
,
то така система має нескінченну множину
розв'язків.
Для таких систем вводять поняття загального розв'язку і фундаментальної множини розв'язків.
Щоб отримати загальний розв'язок такої системи, необхідно визначити базисні невідомі. Їх кількість дорівнює рангу матриці системи. Усі інші невідомі вважаються вільними і вибираються довільно, а r базисних невідомих визначає однозначно через вільні невідомі.
Щоб отримати фундаментальний розв'язок системи, необхідно у загальний розв’язок замість вільних невідомих підставити елементи рядків одиничної матриці, ранг якої дорівнює числу вільних невідомих.
Найбільш універсальним методом розв'язання системи (2.1) є метод Гаусса. Його можна застосовувати незалежно від того, сумісна система чи ні. Суть методу полягає в послідовному виключенні невідомих з рівнянь системи шляхом застосування до них елементарних перетворень.
2.6 Метод Жордана-Гаусса для розв`язання систем лінійних рівнянь
Розглянемо систему лінійних рівнянь (2.1). Із цією системою пов'язана таблиця жорданових перетворень, що має вигляд
Таблиця 2.1
|
|
|
…… |
|
|
|
|
|
|
…… |
|
|
|
|
|
|
…… |
|
|
|
|
….. |
…… |
…… |
…… |
….. |
|
|
|
|
|
|
|
|
Розв'язок системи рівнянь зводиться до перетворення жорданових таблиць. Перехід від однієї таблиці до іншої відбувається за допомогою двох кроків:
1-й крок.
Серед елементів таблиці
![]() вибирають розрахунковий елемент. Рядок
і стовпець, на перетині яких розташовано
розрахунковий елемент, називаються
відповідно розрахунковим
рядком
та стовпцем.
вибирають розрахунковий елемент. Рядок
і стовпець, на перетині яких розташовано
розрахунковий елемент, називаються
відповідно розрахунковим
рядком
та стовпцем.
На першому кроці всі елементи розрахункового рядка діляться на розрахунковий елемент. Далі всі елементи розрахункового стовпця, окрім розрахункового елемента, заміняють нулями.
2-й крок.
Усі інші елементи жорданової таблиці
обчислюють за правилом прямокутника.
Нехай
– розрахунковий елемент. Нам потрібно
отримати на місці елемента
![]() новий
новий
![]()
![]() .
(2.15)
.
(2.15)
Розрахунки зображені на схемі.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
″–″ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
″–″ |
|
|
|
″–″ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Після перетворень і отримання другої таблиці вибирають новий розрахунковий елемент і відбувається перехід до третьої таблиці й т.д. Жорданові перетворення закінчуються після визначення розрахункових елементів, кількість яких дорівнює рангу матриці системи.
Розв'язання системи в таблицях інколи називають методом жорданових виключень.
Примітка. Двічі в одному рядку вибирати розрахунковий елемент недоцільно.
Приклад
2.1.
Знайти
ранг матриці
 .
.
Розв'язок.
Знайдемо ранг матриці. Мінор першого
порядку, розміщений у верхньому куті
матриці
не дорівнює нулю (![]() ).
Мінор другого порядку також не дорівнює
нулю:
).
Мінор другого порядку також не дорівнює
нулю:
![]() .
.
Всі мінори третього порядку матриці дорівнюють нулю:
 ,
,
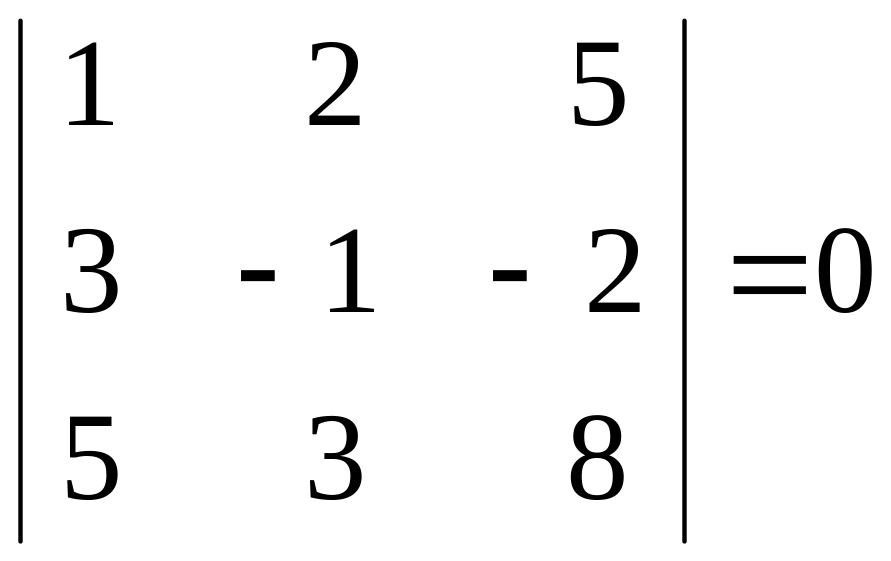 ,
,
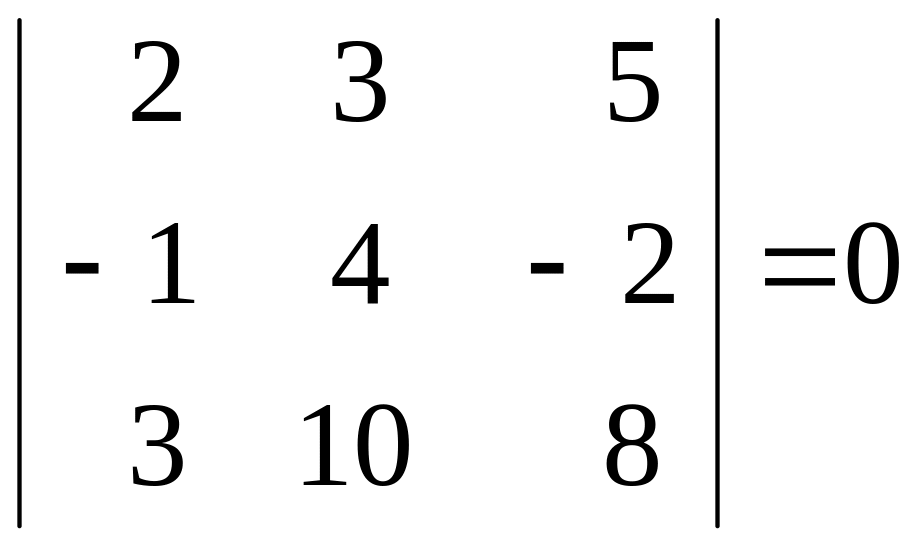 ,
,
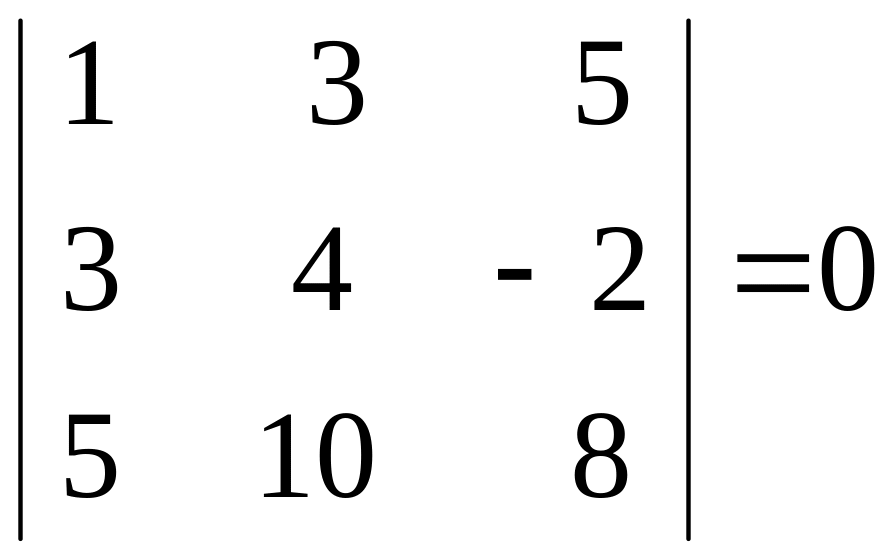 .
.
Звідси,
![]() .
.
Знайдемо ранг матриці за допомогою елементарних перетворень матриці.
 Отже,
.
Отже,
.
Приклад 2.2. Дослідити на сумісність систему рівнянь і у випадку сумісності розв'язати її: а) за формулами Крамера; б) за допомогою оберненої матриці (матричним методом); в) методом Гаусса.
![]()
Розв'язок. Скористаємось формулами (2.2), (2.3). Обчислимо визначник системи:
 тобто
система сумісна.
тобто
система сумісна.
а)
Знайдемо розв'язок за формулами Крамера.
Для цього знайдемо
![]() :
:

Підставляючи знайдені значення визначників до формул Крамера, одержуємо розв'язок системи
![]()
б) Знайдемо розв'язок системи матричним методом

Оскільки визначник матриці системи відмінний від нуля, то матриця А має обернену, і розв'язок системи згідно (2.3) має вигляд .
Для
обчислення оберненої матриці
![]() ,
скористаємось формулою (1.3) та обчислимо
алгебраїчні доповнення елементів
матриці А:
,
скористаємось формулою (1.3) та обчислимо
алгебраїчні доповнення елементів
матриці А:
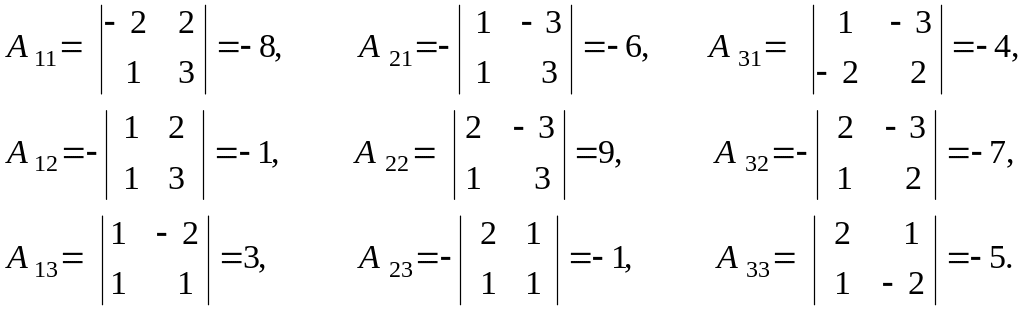
Оберненою матрицею
системи є матриця
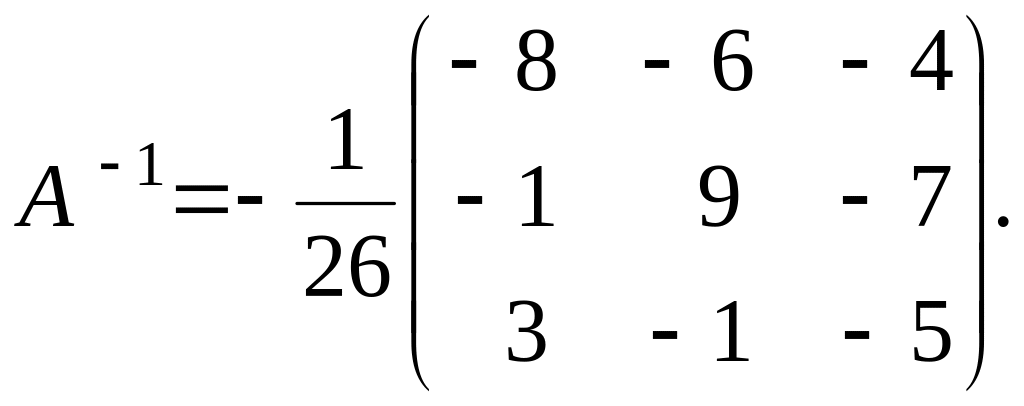
Матричний розв'язок системи має вигляд:

звідки
![]()
в) Розв'яжемо систему методом Гаусса. Метод Гаусса – це метод послідовного виключення невідомих. Для зручності випишемо розширену матрицю з коефіцієнтів при невідомих і стовпчика вільних членів і піддамо її елементарним перетворенням.
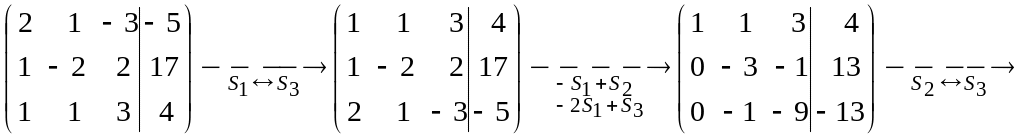

Останній матриці відповідає трикутна система, що еквівалентна даній.
![]()
Приклад 2.3. Розв'язати систему
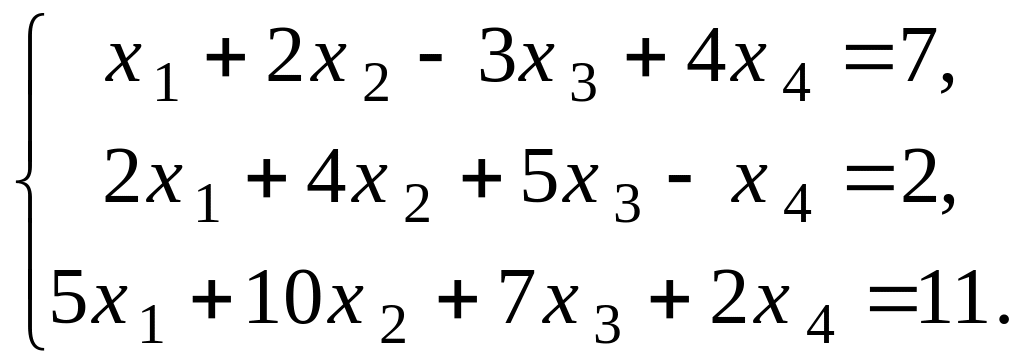
Розв'язок. Знайдемо ранги матриць та :
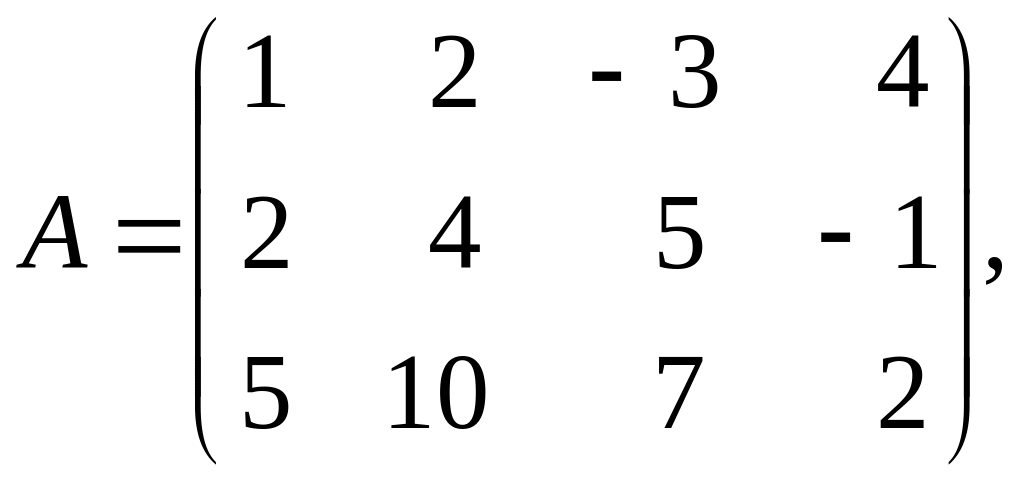
 .
.

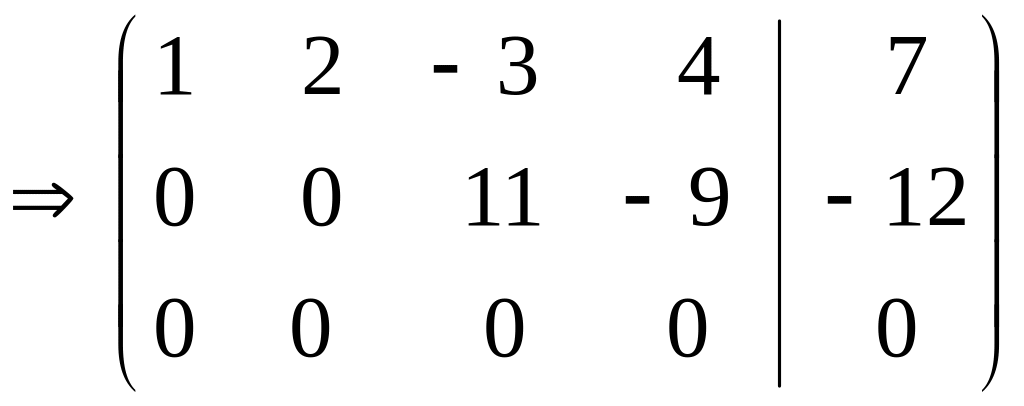 .
.
Одержимо
![]() .
Отже, система сумісна.
.
Отже, система сумісна.
З
останньої матриці перетворень видно,
що в якості базисного мінора можна
взяти, наприклад, мінор
![]() .
Так як
.
Так як
![]() ,
то
,
то
![]() .
При такому виборі мінора М
базисними невідомими є
.
При такому виборі мінора М
базисними невідомими є
![]() .
.
Дана система еквівалентна системі
![]() або
або
![]()
За формулами Крамера знаходимо:


Отже, множина розв'язків має вигляд:
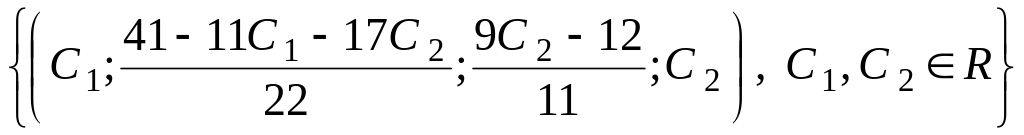 .
.
Приклад 2.4. Розв'язати систему лінійних рівнянь методом жорданових виключень
![]()
Розв'язок. Записуємо систему у вигляді таблиці.
Таблиця 2.2
|
|
|
|
|
|
|
|
2 1 1 |
1 –2 1 |
–3 2 3 |
–5 17 4 |
–5 18 9 |
При переході до другої таблиці згідно із алгоритмом вибираємо за розрахунковий елемент. |
|
0 1 0 |
5 –2 3 |
–7 2 1 |
–39 17 –13 |
–41 18 –9 |
При
переході до третьої таблиці за
розрахунковий вибираємо елемент
|
|
0 1 0 |
26 –8 3 |
0 0 1 |
–130 43 –13 |
–104 36 –9 |
При переході до четвертої таблиці за розрахунковий вибираємо елемент . |
|
0 1 0 |
1 0 0 |
0 0 1 |
–5 3 2 |
–4 4 3 |
У результаті трьох кроків жорданових перетворень система транспонувалась у наступну |
|
|
|
|
|
|
|
Ми отримали розв'язок задачі.
Елемент
використовують для перевірки правильності
розбрахунків на кожному кроці. Якщо
сума елементів за рядком співпала з
розрахунковим значенням
,
то це означає, що серед нових елементів
![]() ,
,
![]() помилково обчислених немає.
помилково обчислених немає.
Приклад 2.5. Розв'язати систему рівнянь методом Гаусса та методом Жордана-Гаусса
![]()
Розв'язок. Випишемо розширену матрицю системи та шляхом елементарних перетворень приведемо її до діагонального вигляду.
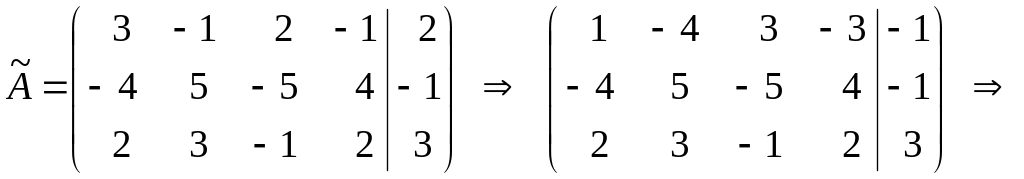

 .
.
rank A = rank = 2. Отже, система сумісна та має нескінченну множину розв'язків.
Після двох кроків перетворень система трансформувалась в наступну
![]()
За
базисні невідомі вибираємо
![]() ,
а за вільні -
,
а за вільні -
![]() .
Фундаментальна система розв'язків має
вигляд:
.
Фундаментальна система розв'язків має
вигляд:
![]()
Поклавши
![]() ,
,
![]() отримаємо розв'язок системи у вигляді
-
отримаємо розв'язок системи у вигляді
-
![]() .
.
Розв'яжемо систему методом Жордана-Гаусса.
Записуємо систему у вигляді таблиці.
Таблиця 2.3
-
База


3
–2
2
–1
5
3
2
–5
–1
–1
4
2
2
–1
3
У системі базисні змінні не визначено. Вводимо до базису .
–3
11
11
1
0
0
–2
5
5
1
–1
–1
–2
9
9
На другому кроці вводимо до базису .
8
–11
0
1
0
0
17
–5
0
0
1
0
7
–9
0
У результаті двох кроків жорданових перетворень ми отримали систему з двома лінійно незалежними рівняннями
![]()
Тут базисні змінні , а вільні – , .
Загальний розв'язок системи має вигляд:
![]()
Базисними
розв'язками системи будуть –
![]() ,
,
![]() .
.





