Второе достаточное условие перегиба.

Если , а , тогда является абсциссой точки перегиба графика функции y=f(x).

Третье достаточное условие перегиба.

Пусть , а , тогда если n – четное число, то является абсциссой точки перегиба графика функции y=f(x).

24 Схема исследование функции с помощью производной.

После того, как найдена область определения функции, установлено, является ли она чётной или нечётной, является ли она периодической, найдены корни рассматриваемой функции, находится её производная.

Точки, в которых производная становится равной нулю, являются критическими точками.

Если ƒ (х₀) = 0 и нашлось такое число k, что все точки  интервала (х₀ – k; х₀ + k) принадлежат области определения функции и для каждого х ≠ х₀ из этого интервала  ƒ (х) > ƒ (х₀), то точка х₀ называется точкой минимума функции  ƒ (х).

Если же для каждого х ≠ х₀ из интервала (х₀ – k; х₀ + k) выполняется неравенство ƒ (х) < ƒ (х₀), то точка х₀ называется точкой максимума функции ƒ (х).

Точки минимума и максимума называются точками экстремума данной функции, а значения функции в этих точках – минимум и максимумом.

Если ƒ (х) > 0 во всех точках некоторого интервала, то функция возрастает на этом интервале.

Если ƒ (х) < 0 во всех точках некоторого интервала, то функция убывает на этом интервале.

Если ƒ (х) – некоторая функция, ƒ ' (х) производная этой функции и ƒ (х₀) = 0, то это ещё не означает, что в точке х₀, функция имеет максимум и минимум.

Пример 1.

Рассмотрим функцию у = 3 (х – 3)³.

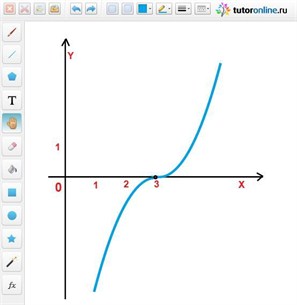у ' = 3 (х – 3)². Производная равна нулю при х = 3. Точка (3; 0) данной функции является критической: она может быть точкой максимума или минимума. Но чтобы эта возможность оказалась реальностью, необходимо убедиться, что в некотором промежутке и левее, и правее рассматриваемой точки, функция либо возрастает, либо убывает.

Установить это можно, отыскав знак производной слева и справа от точки (3; 0). Если на каком-то промежутке слева у ' > 0, а справа у ' < 0, то в рассматриваемой точке функция достигает максимума; если слева у ' < 0, а справа у ' > 0, то в рассматриваемой точке функция достигает минимума.

В рассматриваемом примере 3 (х – 3)² > 0 и слева, и справа от точки (3; 0). Следовательно, ни максимума, ни минимума в этой точке нет. График рассматриваемой функции имеет вид как на рис. 1.

Пример 2.

Установим, имеются ли максимумы или минимумы у функции ƒ (х) = 3/4 х⁴ + 2/3х³ – 1,5х² – 2х.

Решение.

Для этого найдём экстремумы (точки в которых производная равна 0) и промежутки монотонности (промежутки, в которых ƒ (х)  > 0 и потому функция возрастает, ƒ (х)  < 0 и потому функция убывает).

Её производная:

ƒ ' (х) = 3х² + 2 х²– 3х – 2 = х² (3х + 2) – (3х + 2) = (3х + 2)(х² – 1) = (3х + 2)(х – 1)(х + 1).

Корнями производной являются числа -1; -2/3; 1.

Следовательно, область определения функции (-∞; 1); (-1; -2/3); (-2/3; 1); (1; ∞).

Остаётся установить, как ведёт себя функция на интервалах, расположенных левее и правее критических точек. Для этого составим таблицу:

x	ƒ ' (x)	ƒ (x)
(-∞; -1)	< 0	убывает
-1	0	3/4 – 2/3 – 3/2 + 2 = 7/12
(-1; -2/3)	> 0	возрастает
-2/3	0	3/4 · 16/81 – 2/3 · 8/27 – 3/2 · 4/9 + 2 · 3/4 = 50/81
(-2/3; 1)	< 0	убывает
1	0	3/4 + 2/3 – 3/2 – 2 = -2 1/2
(1; ∞)	> 0	возрастает

Ответ: максимума функция достигает в точке (1; 7/12) и в точке (1; -2  1/12). В точке (2/3; 50/81) – минимум функции.

25 Понятие первообразной функции. Понятие неопределенного интеграла.

Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Неопределённый интегра́л для функции  — это совокупность всех первообразных данной функции

Функция F (х) называется первообразной функцией для  данной функции f (х) (или, короче, первообразной данной функции f (х)) на данном промежутке, если на этом промежутке . Пример. Функция  является  первообразной функции на всей числовой оси, так как   при любом х. Отметим, что вместе с  функцией первообразной для является любая функция вида , где С —  произвольное постоянное число (это следует из того, что производная постоянной равна нулю). Это свойство имеет место и в общем случае.  

Теорема 1. Если и — две  первообразные для функции f (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу. Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной  функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С. Выражение F (х) + С, где F (х) —  первообразная функции f (х) и С — произвольная  постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом , причем f (х) называется подынтегральной функцией ; — подынтегральным выражением, х — переменной  интегрирования; ∫ — знак неопределенного интеграла. Таким образом, по определению если . Возникает вопрос: для всякой ли функции f (х) существует первообразная, а значит, и  неопределенный интеграл? Теорема 2. Если функция f (х) непрерывна на [a ; b], то на этом отрезке для функции f (х) существует первообразная. Ниже мы будем говорить о первообразных лишь для непрерывных функций. Поэтому  рассматриваемые нами далее в этом параграфе  интегралы существуют.  

26 Основные свойства неопределенного интеграла, основные табличные интегралы (формулы).

1) Производная неопределенного интеграла равна подынтегральной функции. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (∫f(x)dx)′=f(x)d∫f(x)dx=f(x)dx  Доказательство:

∫f(x)dx=F(x)+C, 

 (∫f(x)dx)′=(F(x)+C)′=F′(x)+0=F′(x)=f(x), 

d∫f(x)dx=(∫f(x)dx)′dx=f(x)dx 

2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. ∫dF(x)dx=F(x)+C . Доказательство:

dF(x)=F′(x)dx=f(x)dx, 

∫dF(x)dx=∫f(x)dx=F(x)+C. 

3) Постоянный множитель можно выносить из под знака интеграла, т.е. ∫kf(x)dx=k∫f(x)dx,k/=0  Доказательство: Пусть F(x) -- первообразная для функции f(x), тогда kF(x) -- первообразная для функции kf(x).

(kF(x))′=0+kF′(x)=kF′(x)=kf(x). 

Таким образом

∫kf(x)dx=kF(x)+C=k(F(x)+C/k)=k(F(x)+C1)=k∫f(x)dx 

4) Неопределенный интеграл от суммы(разности) двух функций равен сумме(разности) интегралов этих функций.

∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx 

Распространяется на n слагаемых. Доказательство:

d[∫f(x)dx±∫g(x)dx]=d∫f(x)dx±d∫g(x)dx= 

=f(x)dx±g(x)dx=[f(x)±g(x)]dx. 

Возвращаясь к той механической задаче, которая была поставлена вначале, можно теперь написать, что v=∫a(t)dt  и s=∫v(t)dt . Предположим для определенности: движение равноускоренное, например, происходит под действием силы тяжести; тогда a=g (если направление вертикали вниз считать положительным) и v=∫gdt=gt+C . Получили выражение для скорости v, в которое, кроме времени t, входит еще и произвольная постоянная С. При различных значениях С получаются и различные значения для скорости в один и тот же момент времени; следовательно, имеющихся данных недостаточно для полного решения задачи. Чтобы получить вполне определенное решение задачи, достаточно знать величину скорости в один какой-нибудь момент времени. Например, пусть известно, что в момент t=t0 скоростьv=v0, подставим эти значения в полученное выражение для скорости v0=gt0+C, откуда C=v0−gt0 , и теперь решение принимает определенный вид: v=g(t−t0)+v0 . Найдем, далее, выражение для пути s. Имеем

s=∫[g(t−t0)+v0]dt=g(t−t0)2/2+v0(t−t0)+C′ 

Неизвестную новую постоянную C′  можно установить, если, например, дано, что путь s=s0 в момент t=t0; найдя, что C′=s0 , получаем решение в окончательном виде s=g(t−t0)2/2+v0(t−t0)+s0 . Значения t0, s0,v0 условно называется начальными значениями величин t,s,v.

Точно так же можно написать: m=∫ρ(x)dx . И здесь при интегрировании появится постоянная C, которая определяется из того условия, что при x=0 и масса m должна обратиться в нуль.