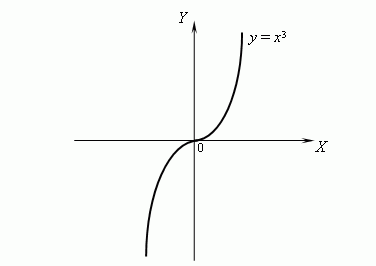Третье достаточное условие экстремума и перегиба.
Теорема 9.9. Пусть
- n ≥ 1 - целое число
- функция имеет производную порядка n в некоторой окрестности точки с и производную порядка n + 1 в самой точке с
- справедливы следующие соотношения:
(2)
Тогда, если n является четным числом, график функции имеет перегиб в точке M(c, f(c)). Если же n является нечетным числом и, кроме того, , функция имеет локальный экстремум в точке с, точнее, локальный минимум при и локальный максимум при .
Доказательство. (для случая экстремума)
Пусть n ≥ 1 является нечетным числом и . Т. к. при n = 1 теорема совпадает с Теоремой 9.2, то достаточно провести доказательство для нечетного n ≥ 3. Для определенности проведем рассуждения для случая . Для случая они проводятся аналогично.
Из условия и из Теоремы 8.9 (Теорема 8.9. Если функция f(x) дифференцируема в точке с и , то эта функция возрастает (убывает) в точке с.), примененной к вытекает, что эта функция возрастает в точке с. Т. к., кроме того, , то это означает, что найдется достаточно малая окрестность точки с, в пределах которой отрицательна слева от с и положительна справа от с. Разложим f'(x) в окрестности точки с в ряд Тейлора с остаточным членом в форме Лагранжа. Мы получим, что для всех x из достаточно малой окрестности точки с между с и x найдется точка ξ такая, что
(3)
Соотношения (2) и условие позволяют переписать (3) в виде
(4)
Т. к. ξ всегда лежит между c и x, то для всех x из достаточно малой окрестности точки с производная отрицательна при и положительна при . При нечетном n число n - 1 является четным, а поэтому вся правая (а, следовательно, и левая) часть (4) для всех x из достаточно малой окрестности с отрицательна слева от с и положительна справа от с.
На основании Теоремы 9.1 это означает, что функция f(x) имеет локальный минимум в точке с.
Случай рассматривается совершенно аналогично.
Вторая часть теоремы доказана.
21 Выпуклость и вогнутость графика функции. Достаточное условие выпуклости и вогнутости графика функции.
Выпуклость и вогнутость
свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f '(x) и f "(х), то первый случай имеет место при условии, что f "(x) ≥ 0, а второй при f "(x) ≤ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.
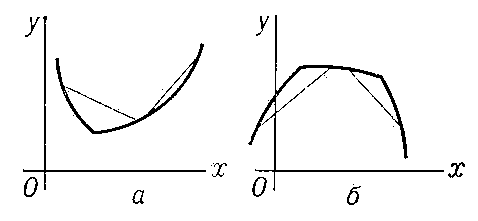
Рис. 1 к ст. Выпуклость и вогнутость.
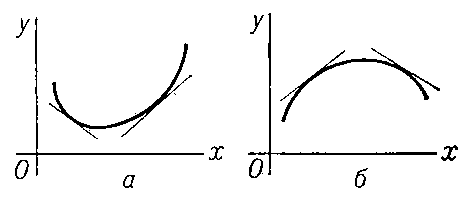
Рис. 2 к ст. Выпуклость и вогнутость.
Определение.
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Определение.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
Посмотрите на чертеж, иллюстрирующий эти определения.
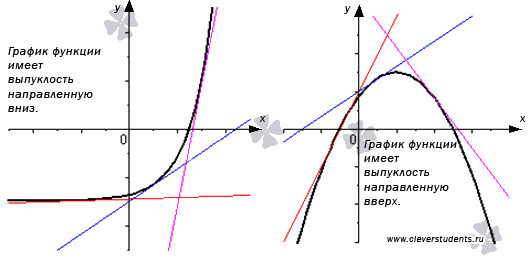
Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если
f
'' (
x
)
>
0 для любого x
(
a,
b
),
то
функция f
(
x
) является
вогнутой
на интервале
( a,
b
);
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
22 Точки перегиба. Необходимое условие перегиба. Критические точки второго рода.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
П р и м е р . |
Рассмотрим график функции y = x3 :
Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x > 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3 является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3. |
