Производная алгебраической суммы функций

выражается следующей теоремой.

Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)' = u'±v'

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

(u — v + w)' = u' — v' + w'

Производную произведения функций определяет

Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

(uv)' = u'v + uv'

Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.

Например, (uvw)' = u'vw + uv'w + uvw'

Производная частного двух функций

выражается следующей теоремой.

Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

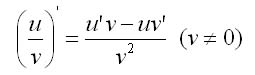
Производную сложной функции выражает

Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.

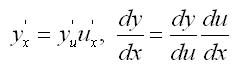
Очень часто в контрольных по математике на производные даются сложные функции, например, y = sin(cos5x). Производная такой функции равна -5sin5x*sin(cos5x)

Производная обратной функции

Еели у = f(x) и х = ф (у) — взаимно обратные дифференцируемые функции, то

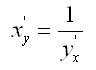
15 Уравнения касательной и нормали к кривой.

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x₀, достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x₀ ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x₀) · (x − x₀) + f (x₀)

Здесь f ’(x₀) — значение производной в точке x₀, а f (x₀) — значение самой функции.

Задача

Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.

Решение

Уравнение касательной: y = f ’(x₀) · (x − x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f (x₀) и f ’(x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x₀) = f (2) = 2³ = 8; Теперь найдем производную: f ’(x) = (x³)’ = 3x²; Подставляем в производную x₀ = 2: f ’(x₀) = f ’(2) = 3 · 2² = 12; Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16. Это и есть уравнение касательной.

Ответ

y = 12x − 16

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

И з определения нормали следует, что ее угловой коэффициент k_n связан с угловым коэффициентом касательной k равенством:

.

Учитывая, что нормаль также как и касательная проходит через точку M(x₀, y₀), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:

Ясно, что если касательная параллельна оси Ox, т.е.f'(x₀) = 0 и ее уравнение имеет вид y= y₀, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x₀.

Примеры.

1. Составить уравнения касательной и нормали к графику функции у = tg²x в точке с абсциссой x₀=π/4.

Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.

Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.

2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2)² + 5 в точке M(2; 5).

y'= x – 2, y'(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .

3. Найти уравнение касательной и нормали к эллипсу в точке M(2; 3).

Найдем y' по правилу дифференцирования неявной функции .

Уравнение касательной: ,т.е. .

Уравнение нормали: , т.е. .

4. Составить уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x₀; y₀), которая соответствует значению параметра t = π/2.

 

При t=π/2x₀= π/2 – 1, y₀=1.

.

Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.

Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.

16 Вычисление производной сложной функции. Производные высших порядков

Хер

17 Возрастание и убывание функции. Необходимое и достаточное условие возрастания и убывания функции.

Вспомним сначала определения возрастающей и убывающей функций.

Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) < f(x₂).

Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) > f(x₂).

Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.

Функция y=f(x) называется постоянной на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.

Р ассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.

(-∞, a), (c, +∞) – убывает;

(a, b) – постоянная;

(b, c) – возрастает.

Применим понятие производной для исследования возрастания и убывания функции.

Теорема 1. (Необходимое и достаточное условия возрастания функции)

1. Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

2. Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].

Доказательство.

1. Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а

Переходя в этом равенстве к пределу при Δx→0, получим , то есть f '(x)≥0.

2. Докажем вторую часть теоремы. Пусть f '(x)>0при всех x  (a,b). Рассмотрим два любых значения x₁ и x₂ таких, что x₁ < x₂. Нужно доказать, что f(x₁)< f(x₂). По теореме Лагранжа существует такое число c  (x₁, x₂), что . По условию f '(x)>0, x₁ – x₂>0 , а это и значит, что f(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающих функций.

Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b]. Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0. Аналогично иллюстрируется и вторая часть теоремы. Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания. Примеры. Определить интервалы монотонности функции. . Область определения заданной функции D(y) = (-∞; 0)(0; +∞). . Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞). Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов. Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1]. . Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).

18 Максимум и минимум функции (точки экстремума). Необходимое условие экстремума.

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Если дифференцируемая функция y=f(x) имеет в точке x= x₀ экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x₀+ Δx)<f(x₀), т.е. Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x₀) ≥ 0 а при Δx → 0 + 0 f'(x₀) ≤ 0. Так как f '(x₀) определяет число, то эти два неравенства совместны только в том случае, когда f '(x₀) = 0.

Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль. Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры. Примеры. y=|x|. Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.   Функция не имеет производной при x=0, так как обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.   Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0. Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Однако, если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум. Например. . Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.

Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.

19 Понятие критической точки. Первое достаточное условие экстремума. Наибольшее и наименьшее значения функции на отрезках.

Критической точкой дифференцируемой функции , где  — область в , называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.

Значение функции в критической точке называется критическим значением. Согласно лемме Сарда, множество критических значений любой -гладкой функции имеет нулевую меру Лебега (хотя критических точек при этом может быть сколько угодно, например, для функции любая точка является критической).

Понятие критической точки допускает обобщение на случай дифференцируемых отображений , и на случай дифференцируемых отображений произвольных многообразий . В этом случае определение критической. точки состоит в том, что ранг матрицы Якоби отображения в ней меньший максимального (равного числу ).

Критические точки функций и отображений играют важную роль в таких областях математики, как дифференциальные уравнения, вариационное исчисление, теория устойчивости, а также в механике и физике. Исследование критических точек гладких отображений составляет один из главных вопросов теории катастроф.

Понятие критической точки обобщается также на случай функционалов, определенных на бесконечномерных функциональных пространствах. Поиск критических точек таких функционалов является важной частью вариационного исчисления. Критические точки функционалов (которые, в свою очередь, являются функциями) называются экстремалями.