1 Матрица. Действия над матрицами.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Для матрицы определены следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (матрицу, имеющую 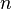столбцов, можно умножить справа на матрицу, имеющую строк);

• в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);

• умножение матрицы на элемент основного кольца или поля (то есть скаляр).

Умножение матрицы на число

Умножение матрицы на число (обозначение: ) заключается в построении матрицы , элементы которой получены путём умножения каждого элемента матрицы на это число, то есть каждый элемент матрицы равен

Свойства умножения матриц на число:

• 1. 1A = A;

• 2. (λβ)A = λ(βA)

• 3. (λ+β)A = λA + βA

• 4. λ(A+B) = λA + λB

Сложение матриц

Складывать можно только матрицы одинакового размера.

Сложение матриц есть операция нахождения матрицы , все элементы которой равны попарной сумме всех соответствующих элементов матриц и , то есть каждый элемент матрицы равен

Свойства сложения матриц:

• 1.коммутативность: A+B = B+A;

• 2.ассоциативность: (A+B)+C =A+(B+C);

• 3.сложение с нулевой матрицей: A + Θ = A;

• 4.существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образует линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.

Умножение матриц

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность ,  — , то размерность их произведения есть .

Свойства умножения матриц:

• 1.ассоциативность (AB)C = A(BC);

• 2.некоммутативность (в общем случае): AB 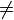BA;

• 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

• 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

• 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

2 Определитель матрицы. Основные свойства определителя.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

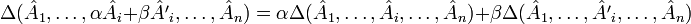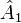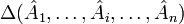• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы,  — определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

3 Методы вычисления определителей. Надеюсь не попадется

Используя основные свойства определителей, вычисление  можно осуществить одним из следующих способов.

1. Метод понижения порядка. Нахождение определителя n-го порядка сводится к вычислению п определителей (n – 1)-го порядка. Метод неэффективен.

2. Нахождение определителя  сводится к вычислению одного определителя (n – 1)-го порядка. Для этого достаточно все элементы, кроме одного, в каком-либо столбце (строке) сделать равными нулю.

3. Приведение определителя к треугольному виду. Состоит в таком его преобразовании, когда все элементы, лежащие по одну сторону главной диагонали, становятся нулями. Полученный определитель равен произведению элементов главной диагонали

4 Обратная матрица. Нахождение обратной матрицы

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.Вторая матрица после применения всех операций станет равна , то есть будет искомой. Сложность алгоритма — .

С помощью матрицы алгебраических дополнений

 — транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

Использование lu/lup-разложения

Матричное уравнение для обратной матрицы можно рассматривать как совокупность систем вида . Обозначим -ый столбец матрицы через ; тогда , ,поскольку -м столбцом матрицы является единичный вектор . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение. Пусть,. Тогда из свойств обратной матрицы можно записать:. Если умножить это равенство на U и L то можно получить два равенства вида и. Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство .

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

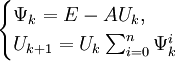
Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору , обеспечивающие выполнение условия (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы (а именно, если A — симметричная положительно определённая матрица и , то можно взять , где 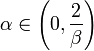; если же A — произвольная невырожденная матрица и , то полагают , где также ; можно конечно упростить ситуацию и, воспользовавшись тем, что , положить ). Во-вторых, при таком задании начальной матрицы нет гарантии, что будет малой (возможно, даже окажется ), и высокий порядок скорости сходимости обнаружится далеко не сразу.