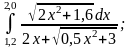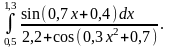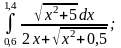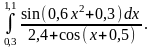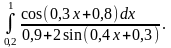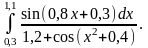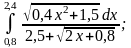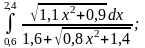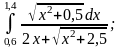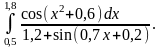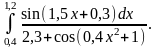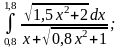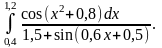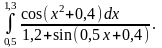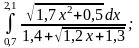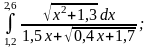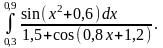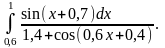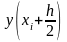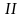Завдання 2
Обчислити інтеграл за формулами лівих та правих прямокутників при
,
оцінюючи точність за допомогою порівняння
одержаних результатів.Обчислити інтеграл за формулою середніх прямокутників, використовуючи для оцінки точності подвійний підрахунок при
Варіанти до завдання 2
№ 1. |
1)
|
2)
|
№ 2. |
1)
|
2)
|
№ 3. |
1)
|
2)
|
№ 4. |
1)
|
2)
|
№ 5. |
1)
|
2)
|
№ 6. |
1)
|
2)
|
№ 7. |
1)
|
2)
|
№ 8. |
1)
|
2)
|
№ 9. |
1)
|
2)
|
№ 10. |
1)
|
2)
|
№ 11. |
1)
|
2)
|
№ 12. |
1)
|
2)
|
№ 13. |
1)
|
2)
|
№ 14. |
1)
|
2)
|
№ 15. |
1)
|
2)
|
№ 16. |
1)
|
2)
|
№ 17. |
1)
|
2)
|
№ 18. |
1)
|
2)
|
№ 19. |
1)
|
2)
|
№ 20. |
1)
|
2)
|
№ 21. |
1)
|
2)
|
№ 22. |
1)
|
2)
|
№ 23. |
1)
|
2)
|
№ 24. |
1)
|
2)
|
№ 25. |
1)
|
2)
|
№ 26. |
1)
|
2)
|
№ 27. |
1)
|
2)
|
№ 28. |
1)
|
2)
|
№ 29. |
1)
|
2)
|
№ 30. |
1)
|
2)
|
_____________________________________________________
Приклад виконання завдання
2)
_____________________________________________________
Для обчислення за формулами лівих та правих прямокутників при розіб'ємо відрізок інтегрування на 10 частин з кроком
Складемо
таблицю значень підінтегральної функції
–
,
в точках поділу відрізка.
|
|
|
0 |
0,4 |
0,7611 |
1 |
0,48 |
0,7451 |
2 |
0,56 |
0,7275 |
3 |
0,64 |
0,7088 |
4 |
0,72 |
0,6898 |
5 |
0,80 |
0,6707 |
6 |
0,88 |
0,6518 |
7 |
0,96 |
0,6334 |
8 |
1,04 |
0,6156 |
9 |
1,12 |
0,5985 |
10 |
1,20 |
0,5822 |
|
||
|
||
В таблиці знайдено значення сум:
,
.
Знайдемо наближені значення інтеграла:
1) за
формулою лівих прямокутників –
;
2) за
формулою правих прямокутників –
.
Результати відрізняються вже в сотих частинах. За остаточне наближене значення інтегралу приймемо півсуму знайдених значень, округливши результат до тисячних:
.
2) Для розв’язування скористаємося формулою середніх прямокутників:
.
Обчислення
виконаємо двічі при
і
відповідно:
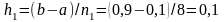і
.
Результати
обчислень наведено в таблицях
і
.
|
|
|
|
Таблиця |
||
|
|
|
|
|||
0 |
0,1 |
0,15 |
0,11914 |
|||
1 |
0,2 |
0,25 |
0,08036 |
|||
2 |
0,3 |
0,35 |
0,04195 |
|||
3 |
0,4 |
0,45 |
0,00487 |
|||
4 |
0,5 |
0,55 |
–0,03026 |
|||
5 |
0,6 |
0,65 |
–0,06316 |
|||
6 |
0,7 |
0,75 |
–0,09397 |
|||
7 |
0,8 |
0,85 |
–0,12323 |
|||
|
|
|
|
|
||
|
|
|
|
Таблиця
|
|
|
|
|
|
||
0 |
0,1 |
0,14 |
0,12300 |
||
1 |
0,18 |
0,22 |
0,09200 |
||
2 |
0,26 |
0,30 |
0,06104 |
||
3 |
0,34 |
0,38 |
0,03065 |
||
4 |
0,42 |
0,46 |
0,00126 |
||
5 |
0,50 |
0,54 |
–0,02685 |
||
6 |
0,58 |
0,62 |
–0,05353 |
||
7 |
0,66 |
0,70 |
–0,07880 |
||
8 |
0,74 |
0,78 |
–0,10288 |
||
9 |
0,82 |
0,86 |
–0,12611 |
||
|
|
|
|
|
|
Знайдемо наближені значення інтеграла
;
.
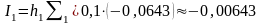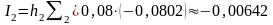Значення
відрізняються п’ятим знаком після
коми, хоча друге значення точніше
першого, але оскільки ми обчислення
вели з п’ятьма десятковими знаками, то
приймаємо
.