
- •4. Числове диференціювання та інтегрування
- •4.1 Теоретичні відомості
- •Обчислення інтеграла і за формулою Сімпсона
- •4.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
- •Варіанти до завдання 1
- •Завдання 2
- •Варіанти до завдання 2
- •Приклад виконання завдання
- •Завдання 3
- •Варіанти до завдання 3
- •Завдання 4
- •Варіанти до завдання 4
4. Числове диференціювання та інтегрування
4.1 Теоретичні відомості
Формули числового диференціювання
а) які
ґрунтуються на першій інтерполяційній
формулі Ньютона
(для
 ,
які знаходяться на початку таблиці):
,
які знаходяться на початку таблиці):
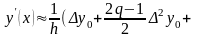

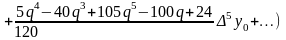 ,
,

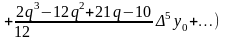 ,
,
де
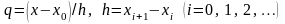 ;
;
б) які ґрунтуються на першій формулі Гаусса (для , які знаходяться всередині та на кінці таблиці):

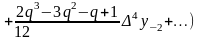 ,
,
 ;
;
в) які ґрунтуються на другій формулі Гаусса:

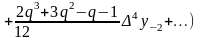 ,
,
 ;
;
г)які ґрунтуються на формулі Стирлінга (для , які знаходяться всередині та на кінці таблиці):

 ,
,
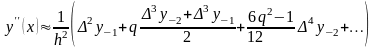 ;
;
д) які ґрунтуються на формулі Бесселя (для , які знаходяться всередині та на кінці таблиці):

 ,
,

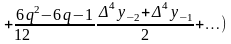 .
.
Формули числового інтегрування.
а) Нехай
відрізок інтегрування
 розбито на
розбито на
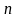 частин з кроком
частин з кроком
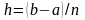 .
Тоді:
.
Тоді:
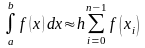 (формула
лівих прямокутників);
(формула
лівих прямокутників);
 (формула
правих прямокутників);
(формула
правих прямокутників);
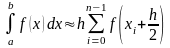 (формула
середніх прямокутників),
(формула
середніх прямокутників),
де
 .
.
Залишкові члени цих формул відповідно дорівнюють
 ,
,
 ,
,
 ,
,
де
 .
.
б) Формула трапецій:
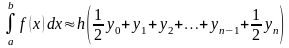 ,
,
де
 ,
причому
,
причому
 .
.
в) Формула Сімпсона (формула парабол) (число - обов’язково парне):
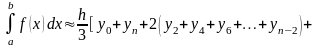
 ,
,
причому
 .
.
в) Формула Ньютона (формула “трьох восьмих”):
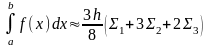 ,
,
де


число розбиттів повинне бути кратним трьом.
Інтеграли з нескінченними межами
Метод зрізу. Для того, щоб наближено обчислити збіжний невласний інтеграл
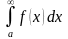
з точністю до ε, представляють його у вигляді
 ,
,
де b вибирають настільки великим, щоб мала місце нерівність
 .
.
Після цього визначений інтеграл

обчислюється за однією з квадратурних формул з точністю до ε/2 і наближено покладають

Приклад 6.1. Обчислити наближено
інтеграл

з точністю до ε = 10-2.
Розв’язування. Вибираєм число b так, щоб виконувалась нерівність
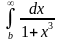 <
< .
.
Зазначивши, що
<
вибираємо b із умови
 =
,
=
,
звідки одержуємо b=10. Наближено приймаємо
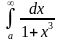
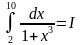
і обчислюємо одержаний визначений
інтеграл з точністю до
 за формулою Сімпсона. В якості кроків
розрахунку виберемо h1=1,
h2=2.
за формулою Сімпсона. В якості кроків
розрахунку виберемо h1=1,
h2=2.
Результати обчислень занесено в табл.
6.1. В останньому рядку наведено суми
 і
і
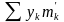 ,
за допомогою яких обчислюємо наближені
значення інтеграла. При кроці h1=1
одержуємо І1=
,
за допомогою яких обчислюємо наближені
значення інтеграла. При кроці h1=1
одержуємо І1=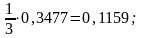 при кроці h2=2
одержуємо І2=
при кроці h2=2
одержуємо І2= .
Ці значення відрізняються менше, ніж
на
.
.
Ці значення відрізняються менше, ніж
на
.
Тому остаточно маємо
= 0,12.
Таблиця 6.1
Обчислення інтеграла і за формулою Сімпсона
-
k
xk
1+x3
yk
mk
mk’
0
2,0
9
0,1111
1
1
1
3,0
28
0,0357
4
2
4,0
65
0,0154
2
4
3
5,0
126
0,0079
4
4
6,0
217
0,0046
2
2
5
7,0
344
0,0029
4
6
8,0
513
0,0020
2
4
7
9,0
730
0,0014
4
8
10,0
1001
0,0010
1
1
Суми
0,3477
0,1809
