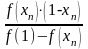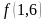- •2. Методи розв'язування нелінійних рівнянь
- •2.1 Теоретичні відомості
- •2.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
- •Відокремити корені аналітично.
- •Варіанти до завдання 1
- •Складемо таблицю знаків функції , приймаючи рівним: а) критичним значенням функції (кореням похідної) чи близьким до них;
- •Завдання 2.
- •Варіанти до завдання 2
- •Завдання 3.
- •Завдання 4.
- •Варіанти до завдання 4
Завдання 2.
Відокремити корені рівняння графічно і уточнити один з них методом хорд з точністю до 0,001.
Відокремити корені рівняння аналітично і уточнити один з них методом хорд з точністю до 0,001.
Варіанти до завдання 2
№1 |
1) ; |
2)
|
№2 |
1)
|
2)
|
№3 |
1)
|
2)
|
№4 |
1)
|
2)
|
№5 |
1)
|
2)
|
№6 |
1)
|
2)
|
№7 |
1)
|
2)
|
№8 |
1)
|
2)
|
№9 |
1)
|
2)
|
№10 |
1)
|
2)
|
№11 |
1) ; |
2)
|
№12 |
1)
|
2)
|
№13 |
1)
|
2)
|
№14 |
1) ; |
2)
|
№15 |
1)
|
2)
|
№16 |
1)
|
2)
|
№17 |
1)
|
2)
|
№18 |
1)
|
2)
|
№19 |
1)
|
2)
|
№20 |
1)
|
2)
|
№21 |
1) ; |
2)
|
№22 |
1)
|
2)
|
№23 |
1) ; |
2)
|
№24 |
1) ; |
2)
|
№25 |
1)
|
2)
|
№26 |
1)
|
2)
|
№27 |
1)
|
2)
|
№28 |
1)
|
2) . |
№29 |
1)
|
2)
|
№30 |
1)
|
2)
|
Приклад виконання завдання 1)
|
1)
Відокремимо корінь графічно. Побудуємо
графіки функцій
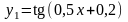 і
і
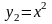 :
будуємо у послідовності – 1.
:
будуємо у послідовності – 1.
 ,
2.
,
2.
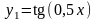 – розтягнення попереднього графіка по
осі
– розтягнення попереднього графіка по
осі
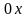 в „2” рази, 3.
в „2” рази, 3.
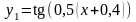 – зміщення осі
на „
– зміщення осі
на „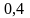 ”;
– парабола.
”;
– парабола.
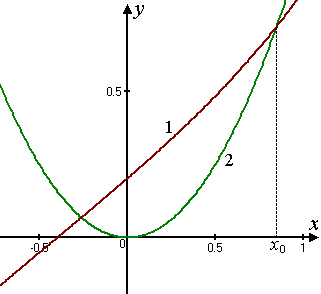
Рис. 3
Графіки
функцій
і
зображено на рис. 3, з якого видно, що
додатній корінь рівняння є
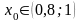 .
.
Щоб
уточнити корінь методом хорд, визначимо
знаки функції
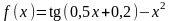 на кінцях проміжку
на кінцях проміжку
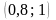 і знак її другої похідної в цьому
проміжку:
і знак її другої похідної в цьому
проміжку:
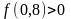 ;
;
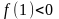 ;
;
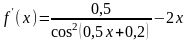 ;
;
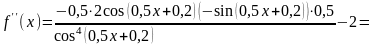
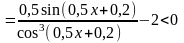 при
при
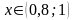 .
.
Оскільки
при
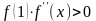 ,
то для розрахунку використовуємо
формулу:
,
то для розрахунку використовуємо
формулу:
 ;
де
;
де
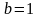 ;
;
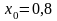 .
.
Обчислення зручно розташувати в таблиці:
|
|
|
|
|
|
|
0 |
0,8 |
-0,1577 |
0,0441 |
-0,2018 |
0,2 |
-0,0437 |
1 |
0,8437 |
|
0,0049 |
-0,1626 |
0,1563 |
-0,0047 |
2 |
0,8484 |
|
0,0005 |
-0,1582 |
0,1516 |
-0,0005 |
3 |
0,8489 |
|
|
|
|
|
Відповідь:
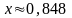 .
.
2) Відокремимо корені аналітично. Маємо
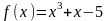 ;
;
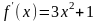 ;
;
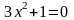 ,
,
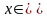 Ø.
Ø.
Складемо таблицю знаків функції :
|
|
|
|
|
|
– |
– |
+ |
+ |
Рівняння
має один дійсний корінь, який належить
проміжку
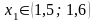 .
.
Щоб уточнити корінь, знаходимо другу похідну
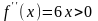 при
при
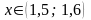 .
Оскільки
.
Оскільки
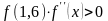 ,
то застосовуємо формулу:
,
то застосовуємо формулу:
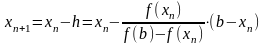 ,
,
де
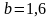 ;
;
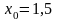 .
.
Розрахунки зручно виконати в таблиці:
|
|
|
|
|
|
|
0 |
1,5 |
0,696 |
-0,125 |
0,821 |
0,1 |
-0,0152 |
1 |
1,5152 |
|
-0,0062 |
0,7022 |
0,0848 |
-0,0007 |
2 |
1,5159 |
|
-0,0006 |
0,6966 |
0,0841 |
-0,00001 |
3 |
1,51591 |
|
|
|
|
|
4 |
|
|
|
|
|
|
Відповідь:
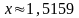 .
.

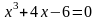 .
.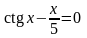 ;
;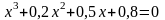 .
.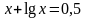 ;
;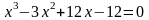 .
.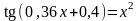 ;
;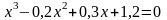 .
.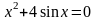 ;
;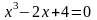 .
. ;
;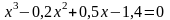 .
. ;
;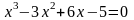 .
.
 ;
;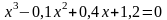 .
. ;
;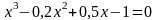 .
.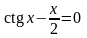 ;
; .
.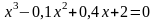 .
.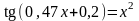 ;
;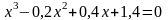 .
.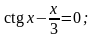 ;
; .
.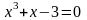 .
.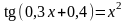 ;
;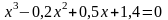 .
.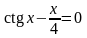 ;
;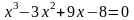 .
.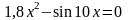 ;
;
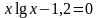
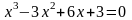 .
.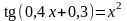 ;
;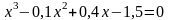 .
.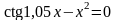 ;
;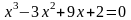 .
.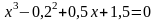 .
.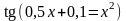 ;
;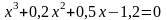 .
.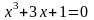 .
.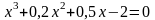 .
.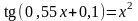 ;
; .
.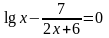 ;
;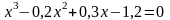 .
.
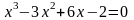 .
.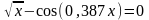 ;
;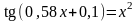 ;
;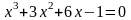 .
.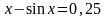 ;
;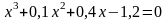 .
.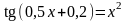 ;
2)
;
2)
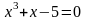 .
.