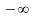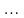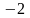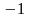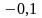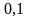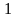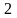- •2. Методи розв'язування нелінійних рівнянь
- •2.1 Теоретичні відомості
- •2.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
- •Відокремити корені аналітично.
- •Варіанти до завдання 1
- •Складемо таблицю знаків функції , приймаючи рівним: а) критичним значенням функції (кореням похідної) чи близьким до них;
- •Завдання 2.
- •Варіанти до завдання 2
- •Завдання 3.
- •Завдання 4.
- •Варіанти до завдання 4
2. Методи розв'язування нелінійних рівнянь
2.1 Теоретичні відомості
Метод
проб (половинного поділу або дихотомії):
Якщо
корінь рівняння
 належить відрізку
належить відрізку
 ,тобто
,тобто
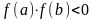 ,
то його ділять навпіл:
,
то його ділять навпіл:
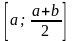 та
та
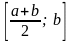 .
Якщо
.
Якщо
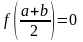 ,
то
,
то
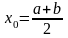 - корінь рівняння. Якщо
- корінь рівняння. Якщо
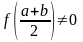 ,
то вибирають ту половину, на якій знаки
,
то вибирають ту половину, на якій знаки
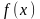 різні і позначають її через
різні і позначають її через
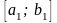 (виконується умова
(виконується умова
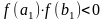 ).
Ітераційний процес (поділ) продовжують
до тих пір, поки довжина відрізка
).
Ітераційний процес (поділ) продовжують
до тих пір, поки довжина відрізка
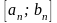 не стане меншою заданої точності
не стане меншою заданої точності
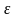 .
Його припиняють і тоді, коли поблизу
кореня значення функції
виявляться порівнюваними з
.
.
Його припиняють і тоді, коли поблизу
кореня значення функції
виявляться порівнюваними з
.
Метод
хорд:
а)
Якщо
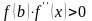 на
на
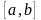 ,
то
,
то
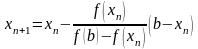 (причому
(причому
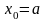 ).
).
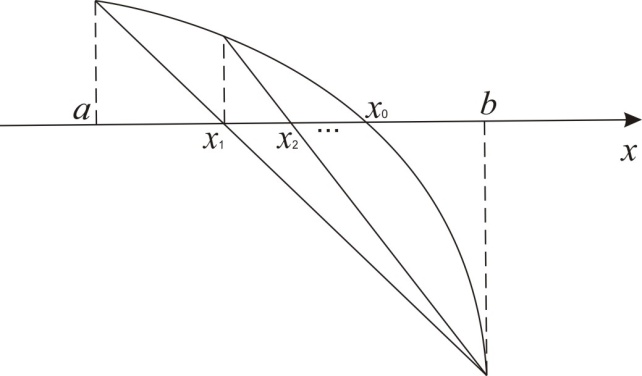
На рис.1
наведено геометричну інтерпретацію
умови
:
як потрібно проводити хорди, точки
перетину яких з віссю
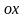 дають
дають
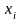 - наближення точного значення кореня
- наближення точного значення кореня
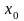 .
.
f(x)
а)
f(x)
б)
Рис. 1
б) Якщо
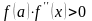 на
,
то
на
,
то
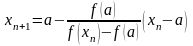 (причому
(причому
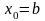 ).
).
На рис.2 наведено геометричну інтерпретацію умови : як потрібно проводити хорди, точки перетину яких з віссю дають - наближення точного значення кореня .
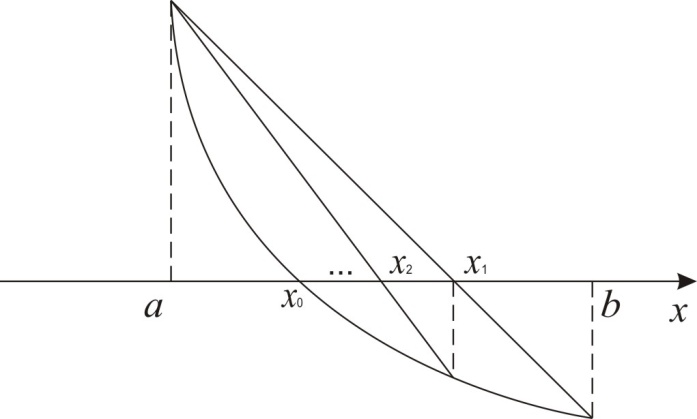
f(x)
а)

f(x)
б)
Рис. 2
Метод
Ньютона (метод дотичних):
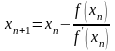 ,
,
причому , якщо .
На рис.3 наведено геометричну інтерпретацію умови : як потрібно проводити дотичні, точки перетину яких з віссю дають - наближення точного значення кореня .
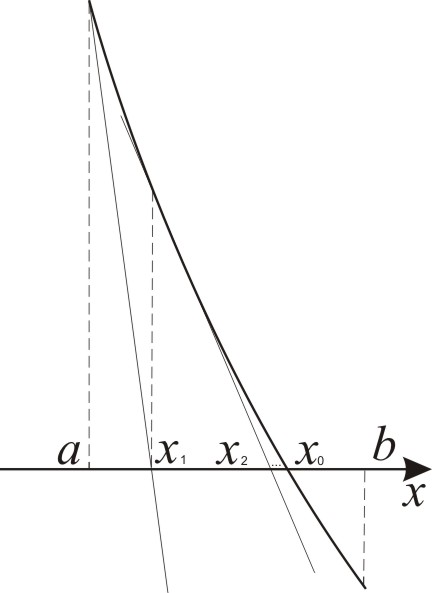
f(x)
f(x)
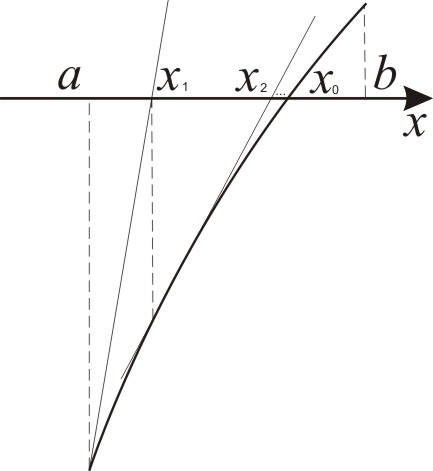
а) б)
Рис. 3
Якщо
на
,
то
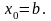
На рис.4 наведено геометричну інтерпретацію умови : як потрібно проводити дотичні, точки перетину яких з віссю дають - наближення точного значення кореня .
f(x)
f(x)
а) б)
Рис. 4
Видозмінена
формула:
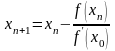 .
.
Комбінований
метод хорд і дотичних.
Нехай
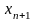 і
і
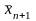 - наближені значення кореня з недостачею
і з надлишком відповідно.
- наближені значення кореня з недостачею
і з надлишком відповідно.
а) Якщо на , то
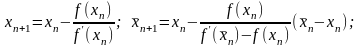
(причому
,
 ).
).
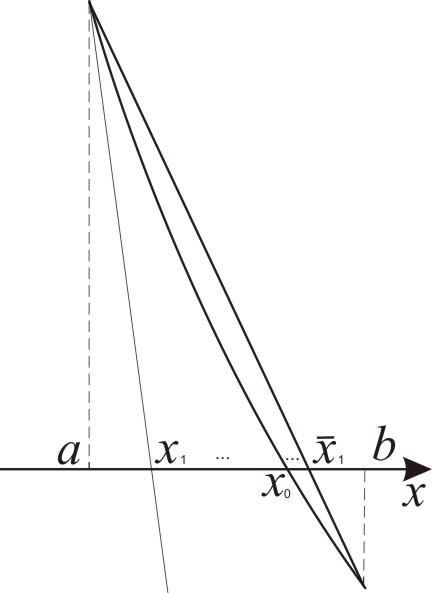
На рис.5
наведено геометричну інтерпретацію
умови
:
як потрібно проводити дотичні і хорди,
точки перетину яких з віссю
дають
та
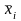 - наближення, відповідно, з недостачею
та надлишком точного значення кореня
.
- наближення, відповідно, з недостачею
та надлишком точного значення кореня
.
f(x)
f(x)

а) б)
Рис. 5
б) Якщо на , то
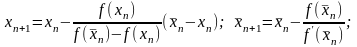
(причому , ).
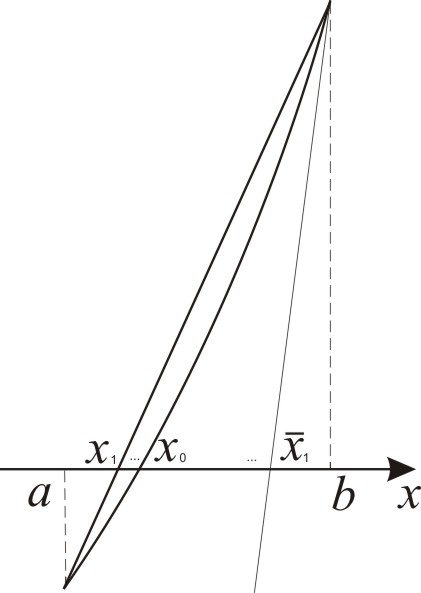
На рис.5 наведено геометричну інтерпретацію умови : як потрібно проводити хорди і дотичні, точки перетину яких з віссю дають та - наближення, відповідно, з недостачею та надлишком точного значення кореня .
f(x)
f(x)
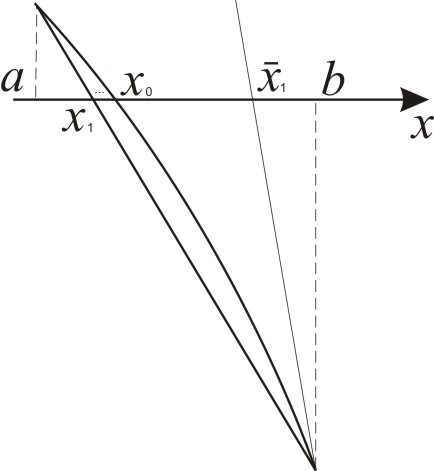
а) б)
Рис. 6
2.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
Відокремити корені аналітично.
Відокремити корені аналітично і уточнити один з них методом проб з точністю
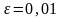 .
.Відокремити корені графічно.
Відокремити корені графічно і уточнити один з них методом проб з точністю .
Варіанти до завдання 1
№1
1)
2)
3)
4)
|
№2
1)
2)
3)
4)
|
№3
1)
2)
3)
4)
|
№4
1)
2)
3)
4)
|
№5 1) ;
2)
3)
4)
|
№6
1)
2)
3)
4)
|
№7
1)
2) ;
3)
4)
|
№8
1)
2)
3)
4)
|
№9
1)
2)
3)
4)
|
№10
1)
2)
3)
4)
|
№11
1)
2)
3)
4)
|
№12
1)
2)
3)
4)
|
№13
1)
2)
3)
4)
|
№14
1)
2) ;
3)
4)
|
№15
1)
2) ;
3)
4)
|
№16
1)
2)
3)
4)
|
№17 1) ; 2) ;
3)
4)
|
№18
1)
2) ;
3)
4) . |
№19
1)
2) ;
3)
4) . |
№20
1)
2) ; 3) ; 4) . |
№21
1)
2) ;
3)
4)
|
№22
1)
2)
3)
4)
|
№23
1)
2) ;
3)
4) . |
№24
1)
2) ;
3)
4) . |
№25
1)
2) ; 3) ;
4)
|
№26 1) ; 2) ; 3) ; 4) . |
№27
1)
2) ;
3)
4)
|
№28 1) ; 2) ;
3)
4)
|
№29
1)
2) ; 3) ; 4) . |
№30
1)
2) ; 3) ;
4)
|
Приклад виконання завдання
1. а)
,
1. б)
2) ;
3)
|
1. а)
Позначимо
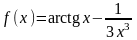 .
Знаходимо похідну
.
Знаходимо похідну
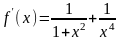 .
Обчислимо корінь похідної:
.
Обчислимо корінь похідної:
 .
Оскільки
.
Оскільки
 ,
то останнє рівняння коренів не має.
,
то останнє рівняння коренів не має.
Оскільки
О.Д.З. рівняння є:
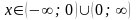 ,
то функція може мати не більше як по
одному корені на кожному із проміжків
,
то функція може мати не більше як по
одному корені на кожному із проміжків
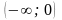 і
і
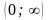 .
.
Знайдемо проміжки, які містять корені, так щоб їх довжина не перевищувала „1”. Для цього складемо таблицю знаків функції :
|
|
|
|
|
|
|
|
|
|
|
|
– |
– |
– |
– |
+ |
– |
+ |
+ |
+ |
+ |
З таблиці
видно, що корені містяться у наступних
проміжках:
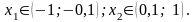
1. б)
Позначимо
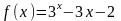 .
.
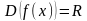 .
Знаходимо похідну
.
Знаходимо похідну
 .
.
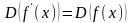 .
Обчислимо корінь похідної:
.
Обчислимо корінь похідної:
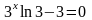 ;
;
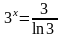 ;
;
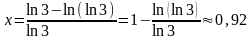 .
.

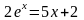 ;
; ;
;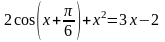 ;
;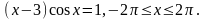
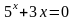 ;
;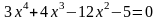 ;
;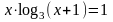 ;
;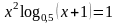 .
.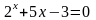 ;
;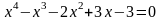 ;
;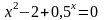 ;
;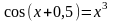 .
. ;
;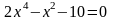 ;
;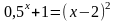 ;
;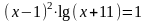 .
.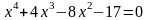 ;
;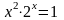 ;
;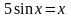 .
.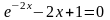 ;
;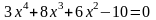 ;
;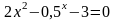 ;
;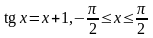 .
.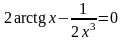 ;
;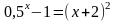 ;
;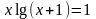 .
. ;
;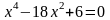 ;
; ;
;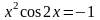 .
.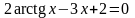 ;
;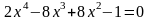 ;
;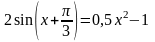 ;
;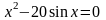 .
.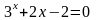 ;
;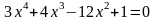 ;
;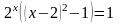 ;
;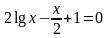 .
.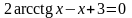 ;
;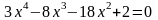 ;
;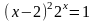 ;
;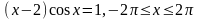 .
. ;
;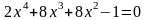 ;
; ;
; .
. ;
; ;
; ;
;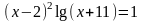 .
.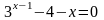 ;
;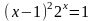 ;
; .
.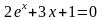 ;
;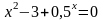 ;
;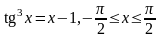 .
. ;
; ;
;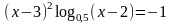 ;
;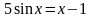 .
.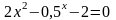 ;
;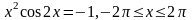 .
.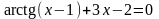 ;
; ;
;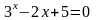 ;
;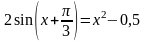 ;
;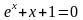 ;
;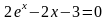 ;
;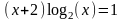 ;
;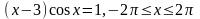 .
.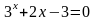 ;
;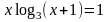 ;
;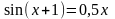 .
.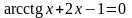 ;
;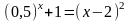 ;
;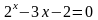 ;
;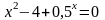 ;
;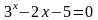 ;
;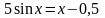 .
.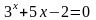 ;
;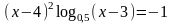 ;
;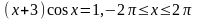 .
. ;
; .
.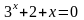 ;
;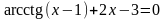 ;
; .
.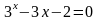 ;
;
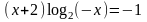 ;
4)
;
4)
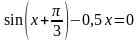 .
.