5. Шкалы рисков

Шкалы рисков используются для сопоставления экономических показателей предприятий эффективностей ценных бумаг с нормативными и для их условного сопоставления с другими предприятиями и всей экономикой.

1.1 . Таблица 9.4

№	Величина отношения	Наименование градации риска
1	0.0 − 0.1	Минимальный
2	0.1 − 0.3	Малый
3	0.3 − 0.4	Средний
4	0.4 − 0.6	Высокий
5	0.6 − 0.81	Максимальный
6	0.8 − 01	Критический

− оптимальный риск;

− ведёт к банкротству.

1.2 . Таблица 9.5

№	Величина отношения	Наименование градации риска
1	0.0 − 0.25	Приемлемый
2	0.25 − 0.5	Допустимый
3	0.5 − 0.75	Критический
4	0.75 − 1	Катастрофический

2. . Таблица 9.6

№	Величина коэффициента вариации	Наименование градаций вариации
1	0.1	Слабая
2	0.1 − 0.25	Умеренная
3	0.25	Высокая

3. . Таблица 9.7

№	Величина	Наименование градаций риска (поведение)
1	< 0.2	Пессимистическое
2	0.2 − 0.4	Осторожное
3	0.4 − 0.6	Средне рискованное
4	0.6 − 0.8	Рискованное
5	0.8 − 1	Высокой степени риска
6	>1	Азартное

4. Систематический риск . Таблица 9.8

№	Значение	Характеристика степени риска
1		Риск отсутствует
2		Риск ниже среднерыночного
3		Риск на уровне среднего по рынку для данного вида вложений
4		Риск выше среднерыночного

9.6. Нахождение оптимальной структуры портфеля с помощью компьютера

Пусть имеется направлений вложения средств с известными эффективностями , то есть возможность вложить средства в ценных бумаг. Считается, что известны также ковариации (корреляционные моменты) между эффективностями по этим ценным бумагам.

Таблица 9.9

Номера ценных бумаг	1	2	…	j	…	n
1			…		…
2			…		…
…	…	…	…	…	…	…
i			…		…
…	…	…	…	…	…	…
n			…		…

Надо найти доли вложения капитала в каждый вид ценных бумаг, чтобы получить ожидаемую эффективность при наименьшей дисперсии (риске) портфеля.

Математическая модель задачи имеет вид:

(9.6)

(9.7)

(9.8)

Например, для трёх ценных бумаг целевая функция имеет вид:

Поэтому задача нахождения структуры оптимального портфеля является задачей квадратичного программирования с двумя ограничениями. Первое уравнение ограничений отражает требуемую эффективность портфеля. Второе показывает, что сумма долей вложения в каждый вид ценных бумаг равна единице. Это стандартная задача квадратичного программирования. Решение такой задачи имеется в программе QSB.

Целевая функция получается нахождением дисперсии:

Здесь , , − эффективность ценной бумаги -го вида, − эффективность портфеля; , − случайные величины. определяются предварительно стандартным способом и по ним рассчитываются исходные характеристики ценных бумаг. . Здесь − количество наблюдений.

Эффективностью ценной бумаги или нормой прибыли в -ом периоде называется величина

, (9.9)

где – цена ценной бумаги в конце -го периода; – цена ценной бумаги в конце -го периода; – дивиденды, насчитанные в -ом периоде.

Рассмотрим методику решения этой задачи.

Пример 9.3

В таблицах 9.10, 9.11 указаны характеристики трёх ценных бумаг, полученные путём обработки временных рядов математические ожидания и корреляционные моменты.

Таблица 9.10 Таблица 9.11

i				1	2	3
1	10		1	8	1	-2
2	5		2	1	2	-1
3	3		3	-2	-1	1

Найти.

1. Задаваясь желаемым значением ожидаемой эффективности портфеля найти структуру оптимального портфеля и соответствующий риск.

2. Найти оптимальную структуру рисковой части портфеля, если принять во внимание, что имеются безрисковые ценные бумаги с эффективностью . Указать эффективность и риск портфеля акций.

3. Найти оптимальное распределение вложений, эффективность оптимального портфеля и риск, если имеется 3 тыс. грн., из которых треть вкладывается в безрисковые ситуации.

Решение. Задачу решаем с помощью программы QSB.

1) Для этого, работая в диалоговом режиме, достаточно внести данные в виде таблицы:

Таблица 9.12 Таблица 9.13

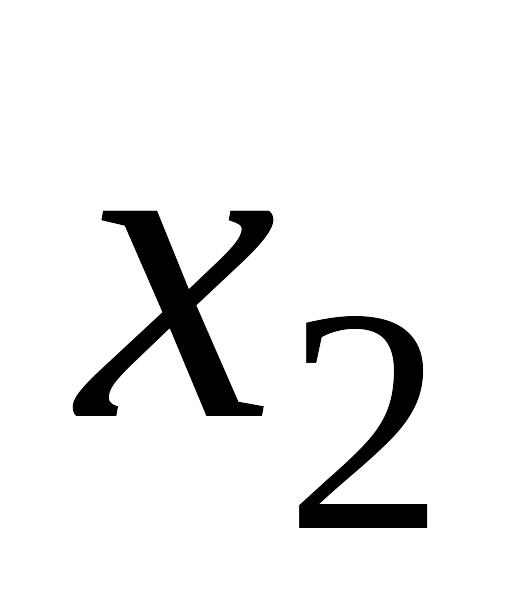
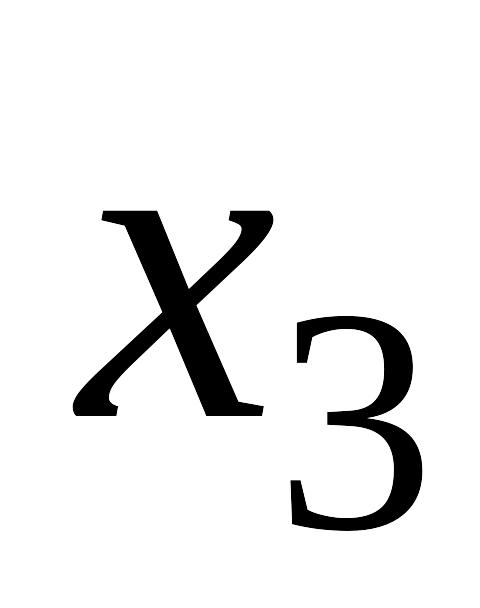
	0	0	0					0	0	0
								8	1	-2
								1	2	-1
								-2	-1	1
				=				10	5	3	=	6
	1	1	1	=	1			1	1	1	=	1

Решая, получаем ответ: или , .

Вывод.

Чтобы иметь эффективность портфеля 6%, при минимальном риске в первые ценные бумаги надо вложить 37.6% инвестиционных средств, во вторые –18.5%, в третьи – 43.9%. При этом соответствующий риск равен

.

В случае наличия безрисковых ценных бумаг с эффективностью изменяем количество переменных на 4 и вносим данные в таблицу.

Таблица 9.14 Таблица 9.15

	0	0	0	0					0	0	0	0
				0					8	1	-2	0
				0					1	2	-1	0
				0					-2	-1	1	0
					=				10	5	3	2	=	6
	1	1	1	1	=	1			1	1	1	1	=	1

Решая, получаем ответ: или . Методика решения указана ниже на стр.72.

Отрицательное число -0.571 можно трактовать, как рекомендацию взять

57.1% от имеющейся суммы в кредит под 2% и вложить вместе с имеющейся

суммой в первые три ценные бумаги, выделяя в каждое вложение соответственно .

2) Найдём структуру рисковой части портфеля.

Если в инвестициях участвуют безрисковые ценные бумаги, то независимо от ожидаемой эффективности портфеля структура рисковой части постоянна.

; (9.10)

.

При этом

,

.

2. Пусть из 3тыс. грн. 1тыс вкладывается под 2%. Оставшиеся 2 тыс. грн. распределяются следующим образом:

(грн) под 10%;

(грн) под 5%;

(грн) под 3%.

Эффективность и риск портфеля соответственно равны

, (9.11)

. (9.12)

Общая структура портфеля такая:

9.6% − I, 17.9% − II, 39.2% − III, 33.3% − безрисковые.

Здесь

Пример 9.4

Эффективности трёх ценных бумаг и эффективность рынка ценных бумаг за последние 12 контролируемых периодов внесены в таблицу 9.16.

Таблица 9.16

Контролируемые периоды	1	2	3	4	5	6	7	8	9	10	11	12
Эффективности первой ценной бумаги	8	9	3	8	20	7	7	9	17	19	9	9
Эффективности второй ценной бумаги	3	7	10	9	3	9	3	20	3	19	3	21
Эффективности третьей ценной бумаги	20	9	10	8	20	19	17	20	17	19	20	21
Эффективности рынка ценных бумаг	20	9	11	9	19	18	17	19	15	21	20	20

Найти:

1. Точечные оценки математических ожиданий ;

2. Ковариации ;

3. Дисперсии ;

4. Оценить риск по дисперсии;

5. Оценить риск по коэффициенту вариации;

6. Оценить риск по систематическому риску;

7. Найти коэффициент риска для третьей ценной бумаги;

8. Сформировать портфель ценных бумаг с эффективностью 12.

Решение. Первые семь вопросов решаем с помощью EXCEL, 8-ой − с помощью программы QSB.

Методические указания к использованию EXCEL.

I ) Набрать таблицу 9.16 числовых данных.

I I) Чтобы найти надо:

1. Выделить первую строку данных.

2. Выбрать на панели .

3. В клетке справа от появившегося числа поставить курсор и набрать последовательно =, выделить курсором клетку слева, /, 12, Enter. Полученное число равно . Указанными действиями мы суммировали все числа в первой строке и подели сумму на количество наблюдений.

4. Протянув виз маленький +, найдём .

I I I) Для определения матрицы ковариаций выделяем массив (4 ×4) клеток.

Чтобы найти надо:

1. Поставить курсор в выделённом массиве в клетку (1,2).

2. Вставка.

3. Функция.

4. Статистические.

5. КОВАР.

6. ОК.

7. Курсор находится в Массив1. Переместив панель, выделить первую строку таблицы 9. 16.

8. Курсор перевести в Массив2.

9. Выделить вторую строку.

10. ОК.

11. В клетке появится число равное .

12. Поступая аналогично, с первой и первой строками, получаем ; с первой и третьей строками, получаем ; со второй и третьей − ; с третьей и четвертой − .

13. Аналогично в других клетках, выделённого массива, получаем остальные ковариации , , …, .

Таблица 9.17

Ц .б.	1	2	3	4	5	6	7	8	9	10	11	12			Ковариации
1	8	9	3	8	20	7	7	9	17	19	9	9	125	10,417	25,576	-0,403	8,556	7,792
2	3	7	10	9	3	9	3	20	3	19	3	21	110	9,167	-0,403	45,806	4,722	6,083
3	20	9	10	8	20	19	17	20	17	19	20	21	200	16,667	8,556	4,722	21,056	19
Рынок	20	9	11	9	19	18	17	19	15	21	20	20	198	16,5	7,792	6,083	19	18,083
															1	2	3	Рын.

Замечание. Всю матрицу ковариации можно получить только одним выделением всего массива данных, используя: сервис, анализ данных, ковариацию.

Полученную таблицу можно скопировать и перенести в другой файл, если не помещается, то в альбомную страницу, копировать экран.

Для решения первых шести вопросов и наглядности, результаты вычислений вносим в таблицу 9.18.

Таблица 9.18

Первая ценная бумаги	10.417	25.576	7.792	18.033	5.057	0.486	0.432
Вторая ценная бумаги	9.167	45.806	6.083		6.768	0.738	0.337
Третья ценная бумаги	16.667	21.056	19		4.589	0.275	1.054

Выводы.

По наиболее рисковая вторая ценная бумага, а наименее − третья.

По наиболее рисковая вторая ценная бумага, а наименее − третья.

По первая и вторая ценные бумаги имеют риск ниже среднерыночного, третья – немного выше среднерыночного, но она ведёт себя как рынок ценных бумаг.

Достичь эффективности 17 по третьей ценной бумаге является азартным поведением.

Структуру оптимального портфеля ценных бумаг с эффективностью 12 находим с помощью WINQSB.