8. Производственные функции в эконометрии

Пример 8.1. Приведены данные о выпуске продукции y, затратах труда x₁ и затратах производственных фондов (ПФ) x₂ за десять лет:

Таблица 8.1

y	4.7	6.0	7.4	7.0	8.2	9.0	11.4	12.6	13.8	15.6
x1	2.4	2.8	3.6	3.3	3.9	4.2	4.8	5. 3	5.8	6.7
x2	4.1	5.5	6.7	6.4	7.5	8.4	11.3	12.4	13.6	15.2

Используя эти данные, требуется:

А) Построить производственную функцию Кобба-Дугласа ;

Б) Рассчитать характеристики:

1) среднюю производительность труда;

2) среднюю фондоотдачу;

3) предельную производительность труда;

4) предельную фондоотдачу;

5) эластичность выпуска продукции по затратам труда;

6) эластичность выпуска продукции по производственным фондам;

7) потребность в ресурсах труда;

8) потребность в производственных фондах;

9) фондовооруженность труда;

10) предельную норму замещения затрат труда производственными фондами;

11) эластичность замещения ресурсов;

В) Найти прогноз выпуска у_np для заданных значений х₁=18 и х₂=32,8.

Решение. Отметим длину ряда данных T и количество регрессоров K

А) Построим производственную функцию Кобба-Дугласа

(8.1)

и рассчитаем ее параметры. Здесь у - величина выпуска продукции; х₁ - затраты труда; х₂ - объем производственных фондов; а₀, а₁, а₂ - параметры, подлежащие определению. Функция Кобба-Дугласа является степенной. Чтобы использовать метод наименьших квадратов, предназначенных для линейных зависимостей, прологарифмируем ее и перейдем к линейной функции.

Наши данные тоже подлежат логарифмированию.

Таблица 8.2

lny	1.54756	1.79177	2.00148	1.94591	2.10413	2.19722	2433613	2.53370	2.62467	2.74727
lnx1	0.87547	1.03962	1.28010	1.19392	1.36098	1.43509	1.56862	1.66771	1.75786	1.90211
lnx2	1.41099	1.70475	1.90210	1.85630	2.01490	2.12823	2.42480	2.51769	2.61007	2.72130

Методом наименьших квадратов находим логарифм функции Кобба-Дугласа.

Зафиксируем найденные коэффициенты:

,

,

.

Округлим полученные константы до десятитысячных, зафиксируем производственную функцию Кобба-Дугласа и построим ее график:

,

,

,

.

y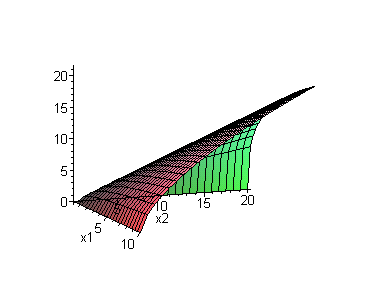

Рис 8.1

Б) Рассчитаем основные характеристики производственной функции.

1. Средняя производительность труда равна:

. (8.2)

Следовательно, с увеличением затрат труда х₁ (при неизменных затратах ПФ х₂)

средняя производительность труда снижается.

Наоборот, увеличение затрат ПФ х₂ (при неизменных затратах труда х₁)

ведет к росту средней производительности труда.

2. Средняя фондоотдача равна

. (8.3)

Таким образом, с увеличением затрат ПФ х₂ (при неизменных затратах труда х₁)

средняя фондоотдача снижается.

Увеличение же затрат труда х1 (при неизменных затратах ПФ х₂)

ведет к росту средней фондоотачи.

3. Найдем предельную производительность труда:

.(8.4)

Следовательно, с увеличением затрат труда х₁ (при неизменных затратах ПФ х₂)

предельная производительность труда снижается.

Наоборот, увеличение затрат ПФ х₂ (при неизменных затратах труда х₁)

ведет к росту предельной производительности труда.

Одновременное изменение обеих переменных может приводить к различным результатам.

4. Найдем предельную фондоотдачу:

.(8.5)

Таким образом, с увеличением затрат ПФ х₂ (при неизменных затратах труда х₁)

предельная фондоотдача снижается.

Увеличение же затрат труда х₁ (при неизменных затратах ПФ х₂)

ведет к росту предельной фондоотдачи.

Одновременное изменение обеих переменных может приводить к различным результатам.

5. Эластичность выпуска продукции по затратам труда:

. (8.6)

Данный показатель указывает на то, что при увеличении затрат труда х₁ на 1%

выпуск продукции у предельно увеличивается на 0,3498%.

6. Эластичность выпуска продукции по производственным фондам:

. (8.7)

Этот показатель указывает на то, что при увеличении ПФ на 1%

выпуск продукции предельно увеличивается на 0,6396%.

7) Производственная функция позволяет рассчитать потребность в одном из ресурсов при заданном объеме выпуска продукции у и величине другого ресурса.

Потребность в ресурсах труда х₁ составляет:

. (8.8)

8) Потребность в производственных фондах х₂ составляет:

. (8.9)

9) Производственная функция позволяет исследовать вопросы соотношения,

замещения, взаимодействия ресурсов. В частности, на основе соотношения х₂/х₁ определяется важный экономический показатель - фондовооруженность труда:

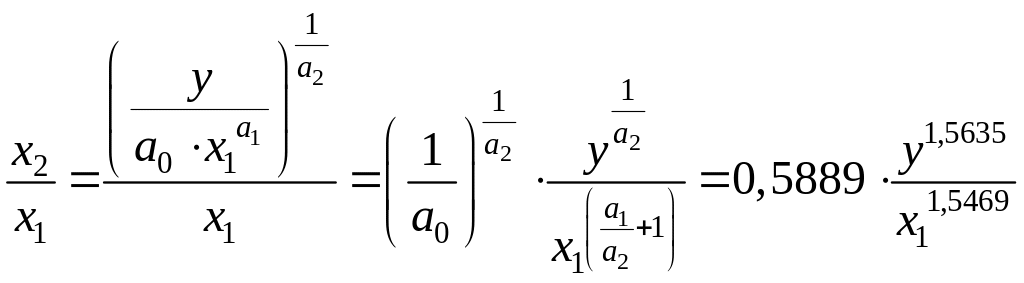. (8.10)

10) Взаимодействующие в рамках производственной функции ресурсы х₁ и х₂

могут замещать друг друга. Предельная норма замещения затрат труда х₁ производственными фондами х₂ равна:

. (8.11)

Предельная норма замещения h зависит не только от параметров а₁ и а₂ производственной функции Кобба-Дугласа, но и от соотношения объемов ресурсов х₁ и х₂.

Знак "минус" означает, что при фиксированном объеме выпуска продукции у

необходимо при уменьшении одного ресурса увеличивать другой.

11) Влияние соотношения объемов ресурсов на предельную норму замещения h находит свое выражение в показателе эластичности замещения ресурсов. Этот показатель определяется как отношение относительных приращений фондовооруженности труда и предельной нормы замещения ресурсов:

(8.12)

Эластичность замещения ресурсов для производственной функции Кобба-Дугласа всегда равна 1. Т.е. изменению фондовооружённости труда на 1% соответствует изменение предельной нормы замещения также на 1%.

В) Найдем прогноз выпуска продукции у_np для заданных значений х₁=18 и х₂=32,8:

.

Задача решена.