5. Метод искусственного базиса (м - метод)

При решении симплекс-методом предполагалось, что среди векторов имеется m – единичных векторов (в каждом уравнении есть базисная переменная – переменная, которая входит лишь в одно уравнение с коэффициентом 1). Если этого нет, то базисные переменные можно формально дописать по следующему правилу. Рассмотрим исходную задачу

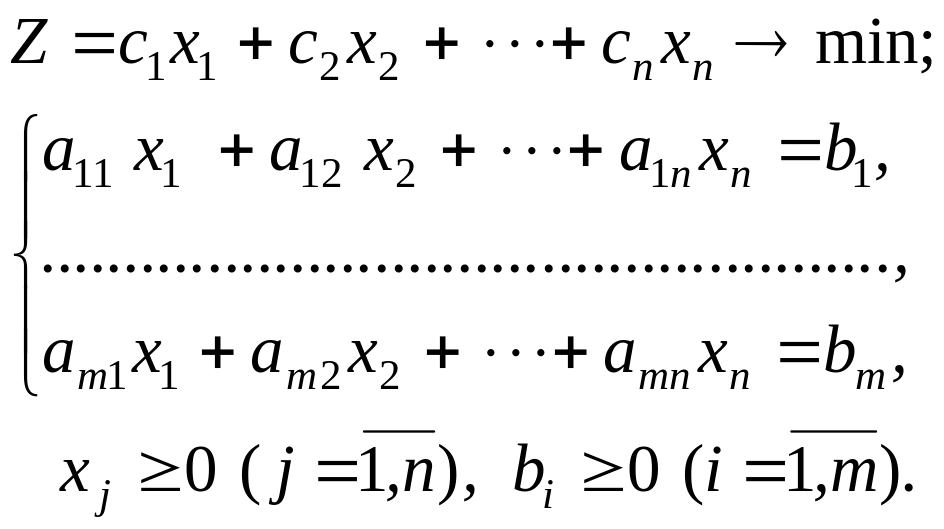(5.1)

Считается, что (если b_i <0, то соответствующее уравнение умножаем на –1).

Составляем расширенную задачу формальным добавлением новых базисных (искусственных) переменных в уравнения, в которых их нет. В целевую функцию их дописываем с большим положительным числом М. Получим расширенную задачу

(5.2)

Ясно, что искусственные переменные должны равняться нулю. Если среди них имеются не равные нулю, то исходная задача несовместная. Или, по-другому, целевая функция расширенной задачи будет неограниченно расти с ростом М и не сможет достичь минимума.

При использовании метода искусственного базиса надо руководствоваться следующим правилом. Ели в оптимальном плане расширенной задачи искусственные переменные равны нулю, то остальные переменные дают решение исходной задачи, если же есть не равные нулю, то исходная задача несовместная.

Замечание. Если на некотором этапе, после выведения искусственных переменных из базиса, возникнет столбец с неположительными членами и положительной оценкой для данного столбца, то . Если в оптимальном плане есть свободный вектор с нулевой оценкой, то вообще оптимальный план не единственный.

Расширенная задача решается обычным симплекс-методом. Числа в индексной строке имеют вид a+bM и их записывают в виде . Поэтому индексную строку записывают в двух уровнях: в (m+1)-ю строку вносят а, а в (m+2) -ю b. Знак числа a+bM совпадает со знаком числа b (если b 0) (например 25- 6М = <0, >0 , -245 +М = >0, >0, <0). Поэтому сначала направляющий столбец выбирают по нижней строке, а после превращения искусственных переменных в свободные оптимизация производится по верхней индексной строке.

Пример 5.1. Решить задачу

(5.3)

Решение. Переходим к канонической форме. Для этого делаем замену ; в первое и второе ограничение дописываем балансовые переменные x₄, x₅; первое ограничение, чтобы применять симплекс-метод, умножим на (-1).

(5.4)

В первое и третье уравнение прибавляем искусственные переменные х₆ и х₇ с коэффициентом равным единице. В целевую функцию их дописываем с коэффициентом М. Получили расширенную задачу.

(5.5)

Задачу решаем симплекс методом. Имеем начальный опорный план

и .

Таблица 5.1

								
															3
						-1	-2	-2	0	0	М	М
				М	1	1	-2	[1]	-1	0	1	0			[1/1]	-1	-2
				0	1	1	2	0	0	1	0	0			
				М	3	1	2	1	0	0	0	1			3/1
					0	1	2	2	0	0	0	0
					4	2	0	2	-1	0	0	1

Покажем, как находится индексная строка.

, ,

, (5.6)

и так далее.

Первый план не оптимален. В нижней индексной строке наибольшую оценку имеют и , Выбираем , так как и этот вектор вводим в базис. Симплексное отношение . Выводим из базиса вектор . Составляем новую симплекс-таблицу.

После выведения из базиса столбцов, которые отвечают искусственным переменным, эти столбцы дальше можно не вычислять (они обведены двойной линией), но при рассмотрении двойственных задач их обязательно вычисляют.

Таблица 5.2

					
											2
				-1	-2	-2	0	0	М	М
	А3	-2	1	1	-2	1	-1	0	1	0	
	А5	0	1	1	2	0	0	1	0	0	1/2
	А7	М	2	0	[4]	0	1	0	-1	1	[1/2]
			-2	-1	6	0	2	0	-2	0
			2	0	4	0	1	0	2	0

Делаем итерации, пока не получим отрицательные оценки в индексной строке.

Таблица 5.3

											4
				-1	-2	-2	0	0	М	М
	А3	-2	2	1	0	1	-1/2	0	1/2	1/2	
	А5	0	0	1	0	0	-1/2	1	1/2	-1/2	
	А2	-2	1/2	0	1	0	[1/4]	0	-1/4	1/4	[2]
			-5	-1	0	0	1/2	0	-1/2 -1	-3/2 -1

Таблица 5.4

				-1	-2	-2	0	0	М	М
	А3	-2	3	1	2	1	0	0	0	1
	А5	0	1	1	2	0	0	1	0	0
	А4	0	2	0	4	0	1	0	-1	1
			-6	-1	-2	0	0	0	0 -1	-2 -1

, . Все искусственные переменные равны нулю, поэтому начальные переменные определяют оптимальный план.

Ответ.

Замечание. Если задача на max, то не обязательно переходить к нахождению min. Можно решать задачу на max, но в этом случае целевую функцию надо записать в виде

. (5.7)

Пример 5.2. Написать двойственную задачу к задаче примера 5.1 и найти её решение.

Решение. Исходная задача:

Любого знака

(5.8)

Двойственная задача к исходной имеет вид:

(5.9)

Решение двойственной задачи: .

.

Покажем решение примера 5.1 в программе WINQSB.

Таблица 5.5

По методике, изложенной в примере 4.3, можно сделать анализ решений исходной и двойственной задач.