Глава 11 Непрерывность функции. Производная и кривизна Понятие предела

Рассматривая вопрос о сумме бесконечно убывающей геометрической прогрессии, о вычислении длины окружности, площади круга и поверхностей и объемов круглых тел, мы уже пользовались понятием предела. Дадим точное определение предела. Пусть задана бесконечная последовательность чисел a₁, a₂, a₃,…,a_n,… Если по мере возрастания номера n члены значения членов последовательности приближаются к некоторому числу а так, что абсолютная величина разности |a_n-a| становится меньше любого наперед заданного числа, то число а называют пределом числовой последовательности a_n при возрастании аргумента (номера) n. Это кратко записывают так:

или или просто a_na

Например, или

Величина a_n, стремящаяся к 0 при бесконечном возрастании n, называется бесконечно малой.

Эти же рассуждения и понятия можно применить и в случае непрерывного аргумента.

Примеры

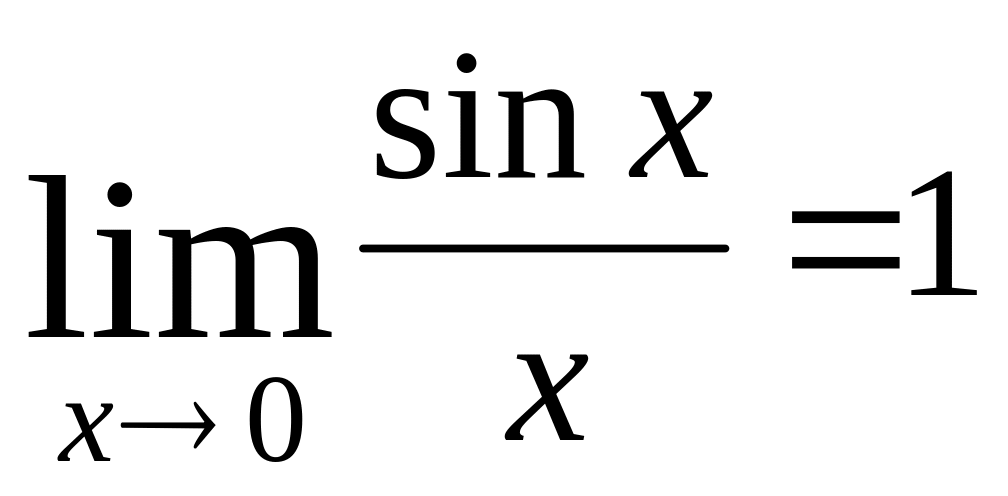1. - I замечательный предел.

Этот предел означает, что при достаточно малых х sinx и х эквивалентны друг другу (напомним, что х – это величина угла, выраженная в радианах) (рис. 1). Это записывают так: sinxх

Смысл I-го замечательного предела состоит в том, что если центральный угол _рад окружности единичного радиуса мал, то длина а полухорды, стягивающей этот угол, и длина дуги s, на которую угол опирается (рис.2), - величины эквивалентные. Действительно, величина угла в радианах – это и есть длина дуги окружности единичного радиуса, на которую угол опирается. А длина полухорды a=sin). Длину окружности L и вычисляют, как предел периметров вписанных n-угольников, когда число сторон n стремится к бесконечности. Если n велико, то _n мало и выполняется sin_n/2_n/2 и a_n2R_n/2=R_n=s. Если L_n периметр многоугольника, то L_n=na_n L.

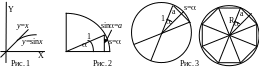
Алгоритм предельного перехода применяется и для определения площади круга. Площадь круга S есть предел площадей n-угольников S_n. S_n складывается из площадей n треугольников равной площади s, вершиной которых является центр окружности, а основанием – сторона многоугольника (рис. 3). По формуле для вычисления площади треугольника получаем s_n=1/2Ra_n.

S_n=ns_n=n1/2Ra_n=1/2RL_n1/2RL=1/2R2R=R²

Архимед за 2тыс. лет до трудов Лейбница и Ньютона об исчислении бесконечно малых, определивших последующее развитие методов математического анализа в Европе, для определения значения числа  применил идею предельного перехода. Он вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников от 6-ти до 96-ти угольника и определил очень узкие пределы для числа : .

2. или -

II замечательный предел. Этот предел мы уже рассматривали, когда делали оценки величины наращенного вклада, когда число периодов начисления процентов по вкладу велико.

Непрерывность функции. Точки разрыва функции

Рассмотрим функцию непрерывного аргумента y=f(x). Пусть при приближении значения аргумента к числу а значение функции приближается к числу А как угодно близко (и может быть даже принимает значение А) (рис. 4).

Тогда говорят, что в точке а существует предел функции f(x), равный А, и это записывается следующим образом:

или

Как а, так и А могут, вообще говоря, принимать значение, равное бесконечности ().

В случаях, когда функция ведет себя по-разному, в зависимости от того, справа или слева мы приближаемся к точке а, говорят о пределе справа и пределе слева и приняты следующие обозначения:

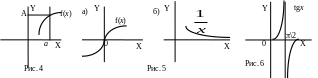
Примеры

1. (рис. 5а)

2. (рис. 5б)

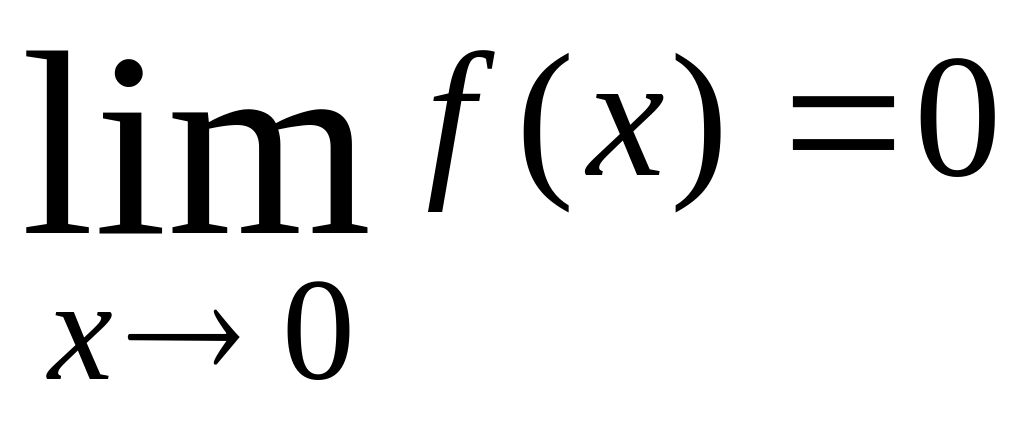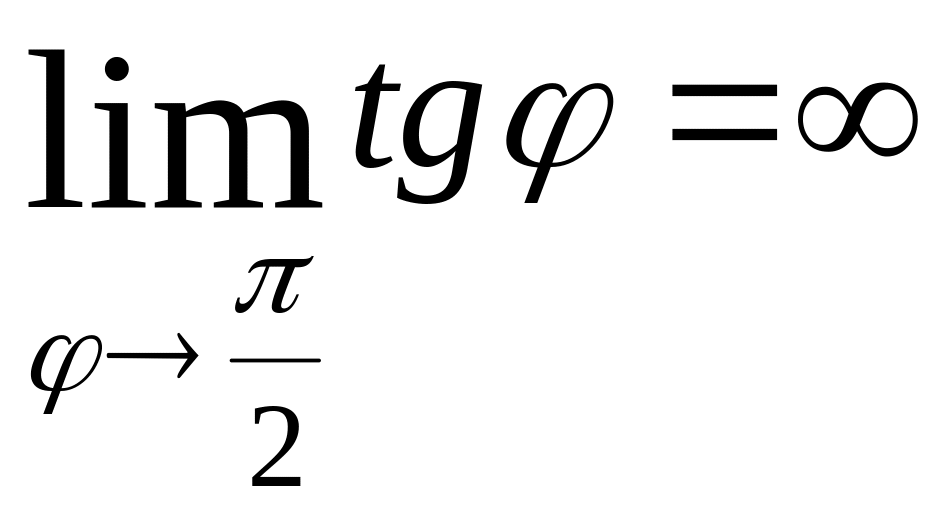3. (рис. 6). Заметим, что при стремлении  к /2 слева, тангенс неограниченно возрастает, а при стремлении  к /2 справа, тангенс неограниченно убывает. Таким образом,

Н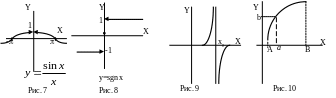 а рисунках 7, 8 и 9 приведены графики функций, имеющих разрыв в точке х₀. На рисунке 10 приведен график функции, которая на отрезке [А,В] не имеет точек разрыва. Такая функция называется непрерывной на отрезке [А,В] (в каждой точке а отрезка функция имеет определенное значение b и ).

Непрерывными являются функции y=x², y=sinx, y=a^x (на всей числовой прямой), y=lnx (при х>0) и т.д.