Шары, эллипсоиды, конусы, цилиндры, параболоиды, гиперболоиды

Уравнение шара: x²+y²+z²=a² - любая плоскость пересекает шар по окружности. Для плоскостей z=h h<a - это окружности x²+y²=а²-h². Из соображений симметрии это верно и для любой другой плоскости, нормаль к которой можно рассматривать в качестве координатной оси)

Уравнение эллипсоида: - любая плоскость пересекает эллипсоид по эллипсу (на рис. 20 приведен чертеж эллипсоида и других обсуждаемых тел).

Уравнение конуса: - вершина конуса в начале координат.

Цилиндрическая поверхность – поверхность, направляющей которой является кривая второго порядка, например, эллипс или парабола, образующей – вертикальная прямая. То есть цилиндр строится следующим образом. На плоскости XOY рассмотрим кривую второго порядка с уравнением F(x,y)=0. Через каждую точку М(х,у,0) линии проведем прямую, параллельную оси Z. Все эти прямые составят поверхность, которая называется цилиндрической. Тип кривой определяет название цилиндра, например:

эллиптический - ,

параболический – y²=2px.

Плоскость z=h пересекает цилиндр независимо от значения z по одной и той же кривой, уравнение которой от z не зависит.

Эллиптический параболоид: - сечения, параллельные плоскости XOY (z=c) – эллипсы (их уравнения ), сечения плоскостями XOZ (y=0) и YOZ (x=0) – параболы x²=a²z и y²=b²z и, вообще, сечения, параллельные оси Z – параболы.

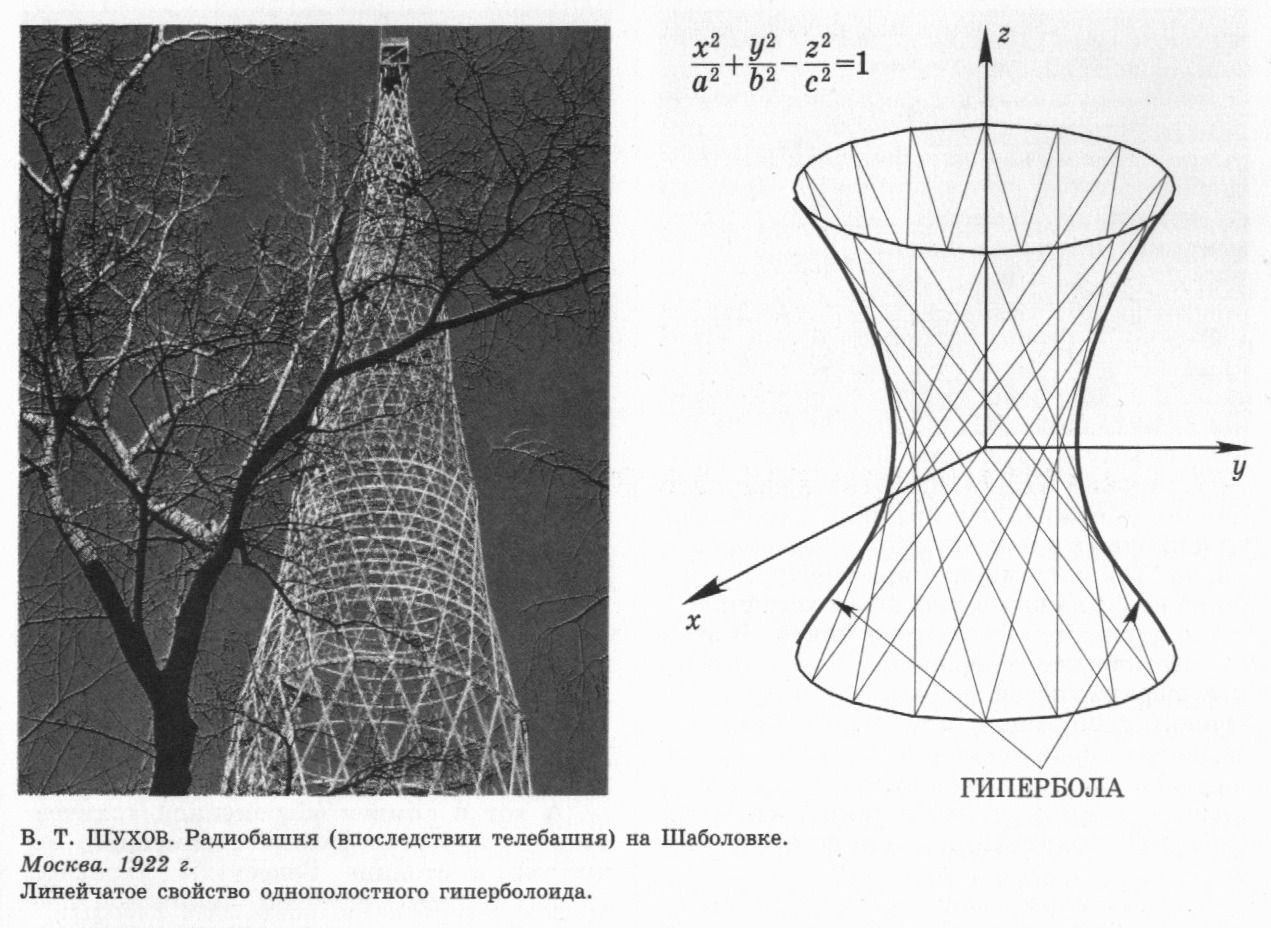
Гиперболоид однополостный: - телевизионная башня Шухова, имеет два семейства прямолинейных образующих (см. ниже).

Д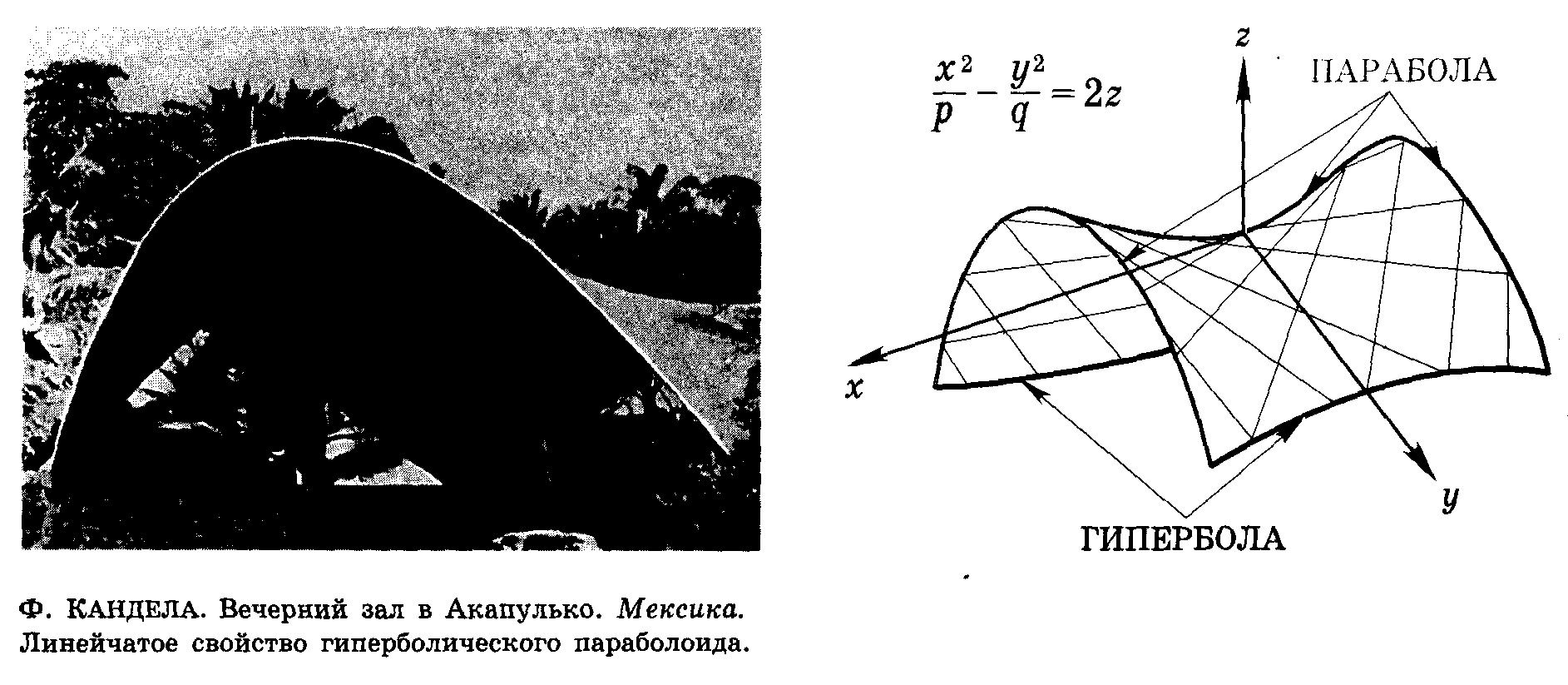 вуполостный гиперболоид:

Гиперболический параболоид: (так называемое седло)

Более подробное описание и рисунки поверхностей второго порядка можно найти в справочниках.

Прямолинейные образующие

Прямолинейной образующей называется прямая линия, целиком лежащая на данной поверхности. Поверхность называется линейчатой, если ее можно образовать движением прямой линии (образующей). Из таких образующих состоят конус, цилиндр, плоскости, однополостный гиперболоид и даже седло.

Телевизионная башня, состоящая из прямолинейных металлических полос (образующих однополостного гиперболоида), дает нам наглядный пример применения на практике линейчатых свойств криволинейной поверхности. Полосы склепываются в местах пересечения двух систем образующих и при малой затрате материала конструкция обладает большой прочностью.

Идея применения в строительной технике конструкции из металлических полос, расположенных так, как расположены прямолинейные образующие однополостного гиперболоида, принадлежала знаменитому русскому инженеру Шухову.

Задачи для самостоятельного решения

1. Постройте график гиперболы.

2. Построить на том чертеже, на котором нарисован график цепной линии (см. задачу 7 гл. 9), по вершине и точке параболу (вершины у обеих линий совпадают, вторая точка параболы лежит на цепной линии).

3. Нарисуйте висящую гирлянду, воспользовавшись для ее линии провиса графиком параболы, заменяющей цепную линию, подобрав масштаб и кусок графика так, чтобы прогиб соответствовал тому, что вы желаете.

4. Постройте эскиз из струй фонтана, имеющих форму парабол.

5. Выберите два произвольных отрезка а и b и постройте на одном чертеже эллипс и овал с выбранными вами полуосями. Отметьте точки фокусов.

6. Постройте изображение шара с экватором и полюсом.

7. Постройте линию, которая получится, если: а) ординаты точек окружности х²+у²=16 уменьшить в 2 раза, не изменяя абсцисс; б) абсциссы точек окружности х²+у²=9 уменьшить в 2 раза, не изменяя ординат. Каковы уравнения полученных линий?

8. Определите радиус окружности, сжатием которой к оси Х получен эллипс . Каковы координаты фокусов эллипса?

9. Составить каноническое уравнение эллипса, если полуоси его соответственно равны 5 и 4. Каковы координаты его фокусов?

10. Определить полуоси эллипсов: а) 25х²+16у²=1, б) х²+4у²=1

11. Постройте линию, определяемую уравнением: 4х²+9у²=36

12. Поверхность задана уравнением . Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0?

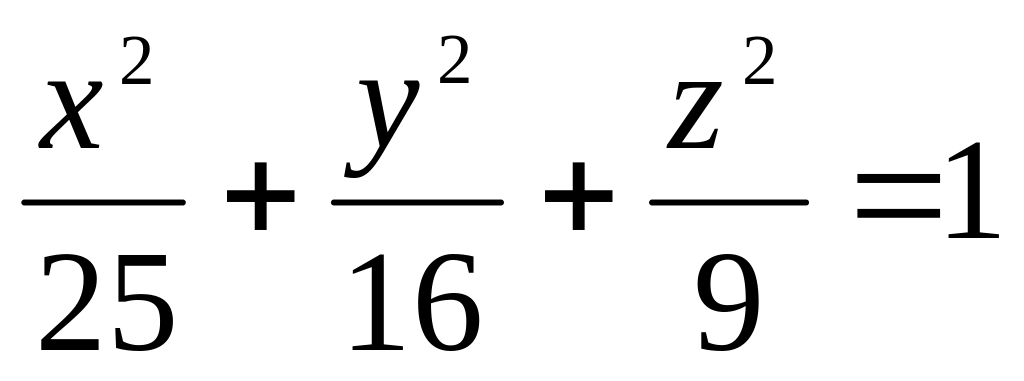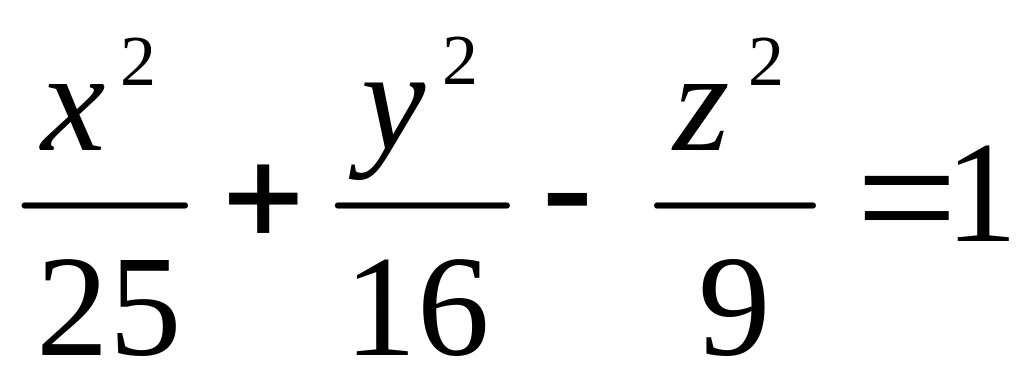13. Поверхность задана уравнением . Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0?