Сравнение сложной и простой схемы

Таким образом, наращенная сумма S_n за n лет по схеме простых процентов S_n=S(1+ni), по схеме сложных процентов S_n=S(1+i)ⁿ. На рисунке 1 графически изображено изменение во времени наращенной суммы по обеим схемам.

Г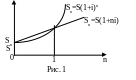 рафик показывает, что для срока, величина которого меньше года, при равных сроках начисления процентов и одинаковых ставках наращения i простые проценты дают наращение больше сложных, для срока, равного году, наращения совпадают, в дальнейшем с каждым новым периодом наращения разница между простыми и сложными процентами увеличивается – по сложной схеме проценты растут гораздо быстрее, так как степенная функция (1+i)ⁿ растет гораздо быстрее, чем линейная 1+ni.

Задачи для самостоятельного решения

1. х=2,37521%. В каких пределах находится значение? Сколько верных знаков?

2. Предполагается, что в древнем Египте для вычисления площади круга использовалась формула 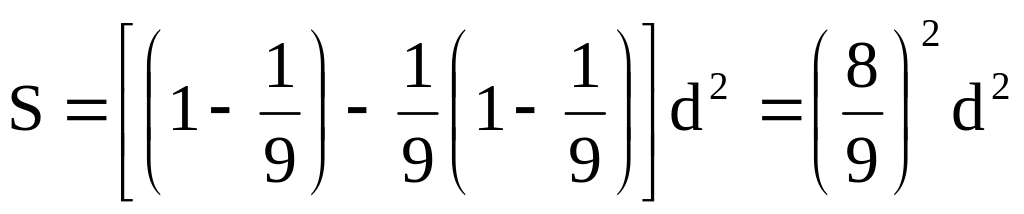. Какова точность (в процентах) получающейся из этой формулы оценки для числа ?

3. Продан товар на 1386 рублей. Получена прибыль 10%. Какова себестоимость товара S?

4. Цену товара снизили на 20%, затем на 15%, затем еще на 10%. На сколько процентов снизили первоначальную цену?

5. Вес задан с точностью 5%. Это пишут так: S(5%). Если вес S=124, то в каких границах находится истинный вес?

6. На сколько процентов увеличится площадь квадрата, если сторону его увеличить на 20%?

7. Число q задано с точностью 1%. Какова точность значения qⁿ для n=2,3,4,5?

8. Банк платит по рублевому вкладу 18% годовых, а по валютному –8%. Цена доллара за год выросла с 25рублей за доллар до 27руб. 50 коп. за доллар. Какой вклад оказался выгоднее?

9. За 8 лет капитал увеличился в 1,5 раза. Какой ставке наращения это соответствует? Указание. Извлечение корня 4-ой, 8-ой, 16-ой, любой 2^к-ой степени можно выполнить с помощью калькулятора: чтобы извлечь корень 4-ой степени, надо нажать на кнопку извлечения корня два раза подряд, 8-ой степени - 3 раза подряд, 16-ой - 4 раза подряд и так далее; это следует из формулы 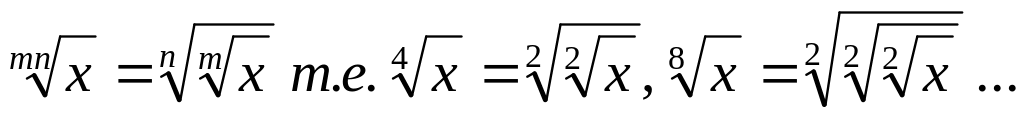). Проверьте. Трехкратное извлечение корня из числа 2 дает: 1+i=1,090508. Таким образом, чтобы решить задачу, надо набрать на калькуляторе 1,5 и 3 раза нажать на кнопку 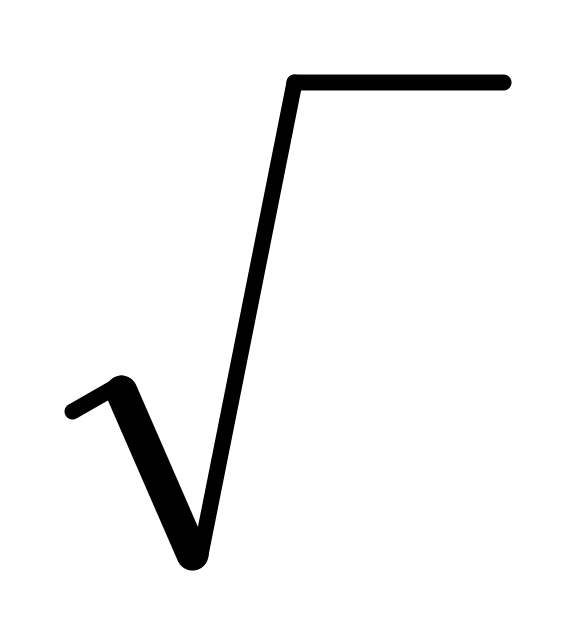, по получившемуся значению установить ставку наращения.

10. Представьте себе, что при рождении Христа на его имя была положена в банк под 1% годовых 1 копейка. Оцените - каков размер этого вклада в настоящее время? Каким будет размер вклада, если копейка была положена под 6% годовых?

Глава 2 Арифметическая и геометрическая прогрессии Метод полной индукции

В основе всякого научного исследования, в том числе и математического, лежат дедуктивный и индуктивный метод. Дедукция – переход от общего к частному. Примером рассуждения такого типа в математике является, например, такое рассуждение: данная фигура прямоугольник; у каждого прямоугольника диагонали равны, следовательно, и у данного прямоугольника диагонали равны. Индукция – вид обобщений, связанных с предвосхищением результатов наблюдений и экспериментов на основе уже имеющихся данных. Индуктивный подход обычно начинается с анализа данных наблюдения или эксперимента. Многократность повторения какого-либо факта приводит к индуктивному обобщению. Конечно, для практики характерны обобщения на основе исследования не всех случаев, а только некоторых. Такие обобщения называются неполной индукцией. Неполная индукция может привести к ошибочным результатам. Если же общее утверждение удается доказать во всех возможных случаях, то такая индукция называется полной. Провести проверку утверждения для бесконечного числа случаев позволяет метод рассуждений, называемый методом математической индукции. Метод состоит в том, что для того, чтобы доказать, что утверждение, зависящее от натурального числа n, справедливо для любого n, надо проверить выполнение 2-х условий:

а) утверждение справедливо при n=1;

б) из справедливости утверждения для конкретного значения n=k вытекает его справедливость и для следующего за ним значения n=k+1.

Смысл рассуждения очень простой. Сначала убеждаемся, что утверждение верно для n=1. Если удается показать, что из справедливости утверждения для конкретного значения n=k вытекает его справедливость и для следующего за ним значения n=k+1, то из того, что утверждение верно для n=1, получается, что оно верно и для следующего натурального значения n=2, из этого следует, что оно верно и для следующего натурального значения n=3 и т.д. Тем самым, оно верно для любого n.

Пример

Доказать, что при любых натуральных n справедливо:

S_n=1+3+5+7+…+(2n-1)=n²

Доказательство:

а)S₁=1=1², следовательно, утверждение верно для n=1.

б)Пусть утверждение верно для натурального числа, n=k, то есть:

S_k=1+3+5+…+(2k-1)=k²

Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, то есть докажем, что:

S_k+1=1+3+5+…+(2k-1)+(2k+1)=(k+1)²

Для этого воспользуемся тем, что для значения k верно:

S_k=1+3+5+…+(2k-1)=k².

S_k+1=1+3+5+…+(2k-1)+(2k+1)=S_k+(2k+1)=k²+2k+1=(k+1)²

Тем самым, формула верна для всех натуральных n.