Изменение уравнения линии при изменении системы координат

1. Сдвиг. При переносе всех точек графика вдоль оси ОХ на величину а и вдоль оси OY на величину b вид графика сохраняется, а значение координат всех точек увеличивается на а и b, соответственно. Следовательно, чтобы уравнение задавало прежнюю форму кривой, необходимо в уравнении компенсировать изменение значений координат соответствующим образом. Например. Пусть центр окружности находится в начале координат. Тогда уравнение окружности имеет вид: х²+у²=R². Перенесем окружность так, что ее центр попадет в точку с координатами С(a,b). Уравнение окружности станет таким: (x-a)²+(y-b)²=R². Из увеличившегося значения координаты мы вычли величину, на которую изменили координату. Координату х мы уменьшили на а, а координату у на b.

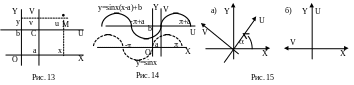
Так как все рассуждения применимы не только к графику функции, а вообще ко всем точкам пространства, эту операцию сдвига можно описать, как переход к новым переменным: u и v. При этом старые и новые переменные связаны соотношениями:

x-a=u, x=u+a,

y-b=v, y=v+b

В системе координат (U,V) центр окружности будет располагаться в начале координат, и уравнение нашей окружности: u²+v²=R². Таким образом, с помощью сдвига системы координат мы привели уравнение линии к более простому виду.

На рисунке 13 показано определение координат произвольной точки М в старой и новой системе координат. Вид графика при сдвиге системы координат не меняется (рис. 14). Сдвиг сохраняет длины отрезков и углы между прямыми

2

Y

. Растяжение (сжатие). Переход от аргумента х к аргументу х (что соответствует изменению масштаба на оси ОХ – растяжению или сжатию в зависимости от значения ) меняет форму графика следующим образом -– растягивает, если <1, или сжимает, если >1 вдоль оси Х в 1/ раз. Действительно, если функция f(x₀)=c, то f(x₁)=c, x₁=х_0, х₁=х₀/. Следовательно, значение с, которое принимала функция в точке х₀, будет приниматься в точке х₁=х₀/, и x₁>x₀, если <1 и x₁<x₀, если >1.

Y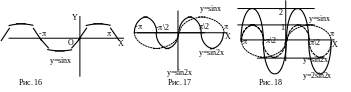

На рисунках 16, 17 и 18 представлены 3 этапа построения графика функции 2sin2x. Сначала строится график функции y=sinx (рис. 16), затем по графику функции sinx строится график функции sin2x (рис. 17) – это функция sinx, сжатая вдвое вдоль оси Х (контрольная точка - если sinx=0 в точке х=, то sin2x=0 в точке х=/2). Затем он растягивается вдвое вверх вдоль оси Y (рис. 18). Заметим, что в приведенном примере множитель 2>1, примененный к координате х, приводит к сжатию вдвое вдоль оси Х, а множитель 2, стоящий перед функцией, - к растяжению вдоль оси Y. Этот эффект связан с тем, что вторая двойка не является множителем, примененным к координате y, если поделить обе части уравнения на 2, то становится видно, что к координате y применен коэффициент 1/2: y=2sin2x, y/2=sin2x. И коэффициент 1/2<1, примененный к переменной y, приводит к растяжению вдвое вдоль оси Y. Таким образом, уравнения: и задают графики такой же формы, что и уравнение y=f(x), но в другом масштабе. Коэффициент а означает растяжение масштаба по обеим осям в а раз, коэффициент b - сжатие в b раз (термины сжатие и растяжение соответствуют a>1 и b>1). Для первого уравнения можно считать, что единицей масштаба является отрезок длины а, для второго уравнения - длины . В уравнении, задающем функцию в неявной форме, обе переменные равноправны и изменение масштаба выглядело бы так: F(ax,by)=0 - сжатие по оси Х в а раз и по оси в b раз (говоря так мы подразумеваем, что а>1 и b>1, для а<1 и b<1 "сжатие" фактически будет означать растяжение).

Примеры

1. Получение графика функции y=a^x из графика функции y=е^x. Воспользуемся формулой определения натурального логарифма: 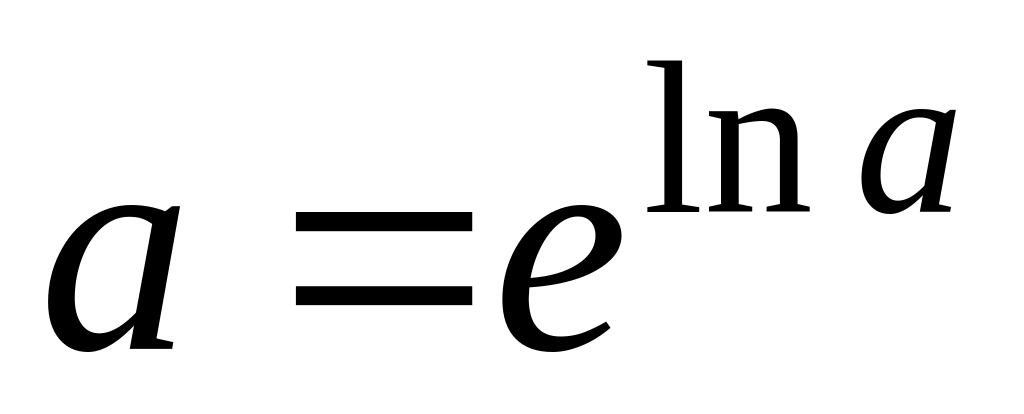. Из нее следует, что: y=a^x=е^xlna, и, следовательно, график функции y=a^x получается из графика функции y=е^x сжатием к оси Y вдоль оси Х с коэффициентом lna (рис. 19а).

2. Получение графика функции y=log_ax из графика функции y=lnx. В силу того, что 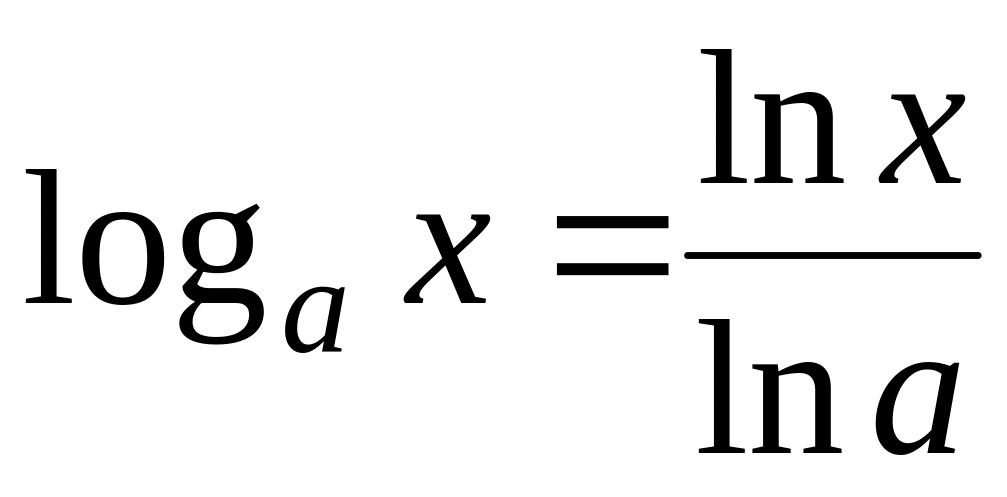, получаем, что график функции y=log_ax получается из графика функции y=lnx сжатием к оси X вдоль оси Y в lna раз (рис. 19б).

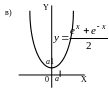3. У равнение цепной линии (гиперболического косинуса) часто пишут в форме: .

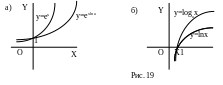
Для того чтобы получить этот график, надо растянуть график y=chx по осям Х и Y в а раз. Или изменить на обеих осях масштаб – не меняя графика, заменить числовые значения, проставив вместо 1 а вместо 2 2а и т.д. На рисунке 19в вместо значений 1 на осях Х и Y проставлены значения а и а, это и есть график функции .

3. Поворот. Повернем оси ОХ и OY на угол  (рис. 15а). Тогда координаты (x,y) всех точек плоскости будут связаны с новыми координатами (u,v) следующими формулами преобразования координат:

x=ucos-vsin,

y=usin+vcos,

а значения новых координат можно вычислить по значениям старых координат по формулам:

u=xcos+ysin,

v=-xsin+ycos.

Например, для поворота на 90 cos90=0, sin90=1, и поворот приводит к тому, что оси ОХ будет соответствовать ось OV (но в обратном направлении), то есть x=-v, оси ОY будет соответствовать ось OU, то есть y=u (рис. 15б).

Повороту на угол =45 соответствует преобразование:

При повороте сохраняются длины отрезков и углы между прямыми, форма графика сохраняется, но уравнение меняется очень сильно.

Пример

Уравнение гиперболы имеет вид: или xy=1. В системе координат (u,v), полученной поворотом на 45º, уравнение гиперболы имеет вид: u²-v²=2.

Задачи для самостоятельного решения

1. Задан отрезок, соединяющий точки (1,2) и (3,4). Написать координаты точек, симметричных заданным точкам относительно начала координат. Построить для заданного отрезка симметрию а) относительно начала координат, б) относительно оси OY.

2. Построить симметрию относительно начала координат для функции, которая задана для x0 следующим образом:

3. Построить график функции y=cos(x-\2).

4. Построить график функции y=cos(x-\2)+1.

5. Построить графики функций у=cos2x и у=cosx\2.

6. Построить график функции у=3cos2x-2.

7. Задана таблица значений функции y=chx на отрезке [0; 2,4].

x	0	0,2	0,4	0,6	0,8	1	1,2	1,4	1,6	1,8	2	2,2	2,4
chx	1	1,02	1,1	1,2	1,3	1,5	1,8	2,15	2,6	3,1	3,4	4,6	5,6

а) Постройте график функции y=chx (цепной линии) на отрезке [0; 2,4].

б) Постройте дополнение этой функции до четной (симметрию относительно оси Y).

8. Через точки (1,2) и (3,4) провести прямую. Построить ее симметрию относительно оси Х и оси Y. Написать уравнения всех трех прямых. Указание. Написать координаты точек, симметричных заданным относительно оси симметрии. Воспользоваться уравнением прямой, проходящей через две заданные точки.

9. Температура по Цельсию и температура по Реомюру связаны друг с другом линейной зависимостью. Температуре таяния льда (0С) соответствует значение 0R, температуре кипения (100С) - 80R. Если взять в качестве аргумента (ось абсцисс) температуру по Цельсию, то температура по Реомюру - линейная функция (ее график прямая линия). Начертить график этой функции – прямую, изображающую график зависимости tR от tC (прямая через 2 точки). Написать уравнение этой прямой и найти графически и аналитически, какая температура по шкале Цельсия соответствует значению tR=-25 (упомянутый в романе "небывалый мороз") и, наоборот, какое значение по шкале Реомюра соответствует значению tC =40 (высокая температура у больного).