Операции над графиками двух функций

Для того чтобы построить график функции, получающейся из двух других с помощью операции сложения (вычитания, произведения), надо нарисовать графики обеих функций, сложить (вычесть, перемножить) их значения в разных точках, результат нанести на чертеж. Чтобы умножить функцию на константу k>1 надо растянуть ее вдоль оси Y в k раз (для k<1, это будет сжатие).

График гиперболического косинуса у=chх, уравнение которого , легко построить по этим правилам на основе графика функции у=е^х.

На рисунке 9б показан метод построения графика гиперболического косинуса из графиков функций е^х и е^-х, жирной чертой показан готовый график. За его форму его еще называют цепной линией. Форму цепной линии принимает гибкая тяжелая нерастяжимая нить, подвешенная в двух точках. Гирлянды, так часто употребляемые в бордюрах, должны иметь форму цепной линии. Цепная линия – четная функция, пересекает ось OY в точке у=1, симметрична относительно оси OY. Она очень похожа на параболу и только в XVIII веке Якоб Бернулли доказал, что форму свободно провисающей цепочки описывает цепная линия, а не парабола.

Примеры решения задач.

На рисунке 9 приведены примеры построения функций:

1. y 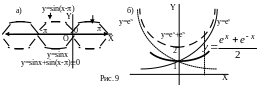=sinx+sin(x-)0, б)

Простейшей функцией, полученной из основных элементарных функций с помощью арифметических операций, является многочлен первой степени y=kx+b (прямая). На примере прямой покажем, как геометрические свойства линии связаны с аналитическими свойствами уравнения. При этом одну и ту же линию мы будем задавать разными уравнениями. Разные формы уравнения позволяют подчеркнуть разные геометрические свойства линии.

Уравнение прямой на плоскости

1. Уравнение прямой, про которую известно, что она отрубает от оси OY отрезок величины b и имеет тангенс угла наклона , равный k ( - угол между прямой и осью ОХ) имеет вид: y=kx+b (рис. 10).

2. Уравнение прямой, про которую известно, что она проходит через данную точку M(x,y), а тангенс угла наклона ее равен k: y-y₁=k(x-x₁) (рис. 11) (угол наклона и точка определяют прямую).

3. Уравнение прямой, про которую известно, что она проходит через 2 точки – M₁(x₁,y₁) и M₂(x₂,y₂):

(рис.12) (2 точки определяют прямую)

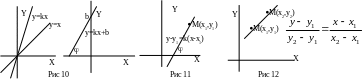
Пример

Температура по Цельсию и температура по Фаренгейту связаны друг с другом линейной зависимостью. Температуре таяния льда (0С) соответствует значение 32F, температуре кипения (100С) - 212F. Если взять в качестве аргумента (ось абсцисс) температуру по Цельсию, то температура по Фаренгейту - линейная функция (ее график прямая линия, проходящая через 2 заданные точки). Написать уравнение этой прямой и найти графически и аналитически, какая температура по шкале Цельсия соответствует значению tF=-40 и, наоборот, какое значение по шкале Фаренгейта соответствует значению tC =40.

Решение:

Напишем уравнение прямой - графика зависимости tF от tC в привычных терминах: tC – x, tF – y. Тогда точки М₁(х₁,у₁) и М₂(х₂,у₂), через которые проходит прямая, имеют координаты: х₁=0, у₁=32; х₂=100, у₂=212. Подставляем эти значения в уравнение прямой, проходящей через 2 заданные точки:

или, вернувшись к шкалам Цельсия и Фаренгейта: .

Отсюда, если tF=-40, то tC=-40º и если tC =40, tF=104

График прямой начертите самостоятельно и проверьте графически правильность решения.