Элементарные функции

Основными элементарными функциями называются следующие функции.

1. Степенные функции: у=х^, где  - действительное число.

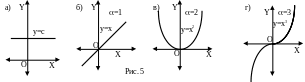
Ее поведение очень сильно зависит от значения .

а) =0, y=const (рис. 5а)

б) N (натуральное, т.е. целое положительное), функция определена на всей числовой оси. На рисунках. 5б,в,г приведены графики функций у=х^ для целых положительных значений =1, =2, =3.

в)  - целое отрицательное число; функция определена при всех значениях х0 (рис. 6а)

г)  - дробное (на рис. 6б,в даны графики степенных функций при =1/2 и =1/3).

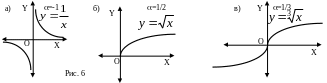
2. Показательная функция: у=а^х определена для всех х и положительна. При а>1 она монотонно возрастает, при 0<a<1 монотонно убывает (рис 7а,б). Для любого а у(0)=а⁰=1

3. Логарифмическая функция: y=log_ax определена для всех x>0. Число а называется основанием логарифма (a>0, a1). Напомним, определение логарифма: 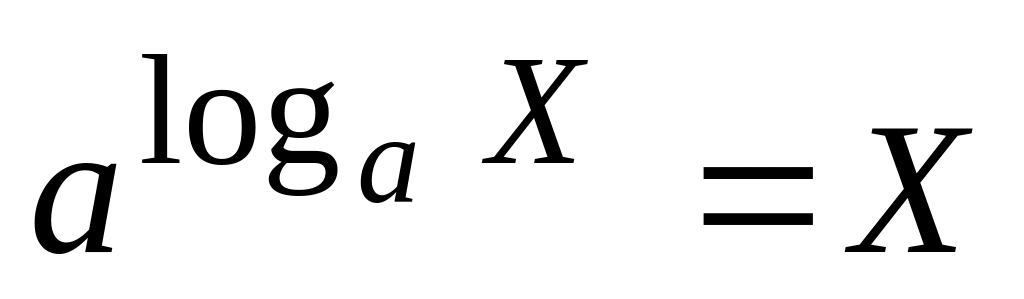и формулу перехода от одного основания к другому: log_aX=log_bXlog_ab=log_bX:log_ba. Его основные свойства: logab=loga+logb, 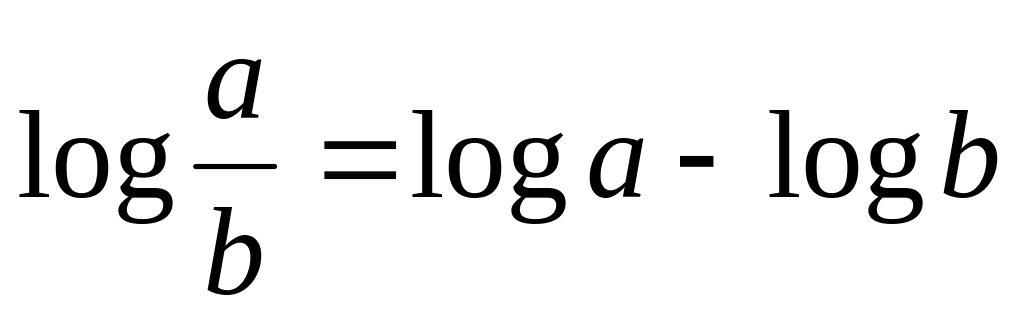, loga^m=mloga,

На практике часто используются логарифмы по основанию 10. Для них принята сокращенная запись lg. При а>1 функция монотонно возрастает, при 0<a<1 монотонно убывает (рис 7в,г). log_a1=0 при любом основании а

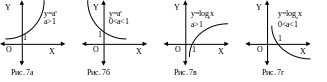
В математике особую роль играют показательная и логарифмическая функция с основанием а=е. Число е – иррациональное число. Его можно записать в виде бесконечной непериодической дроби е=2,71828182845… Логарифм по основанию а=е называют натуральным и записывают обычно в виде y=lnx. Показательную функцию y=e^x называют экспоненциальной функцией, иногда ее записывают так: у=ехрх. Заметим, что a^x=e^xlna (в силу того, что по определению логарифма a=e^lna).

Кроме названия функции, указания операций (+, -, , :) и основных величин, обозначаемых через x, y, z,…, в формулу могут входить константы и параметры – константы, значения которых не заданы. Их обычно обозначают латинскими буквами a, b, c,… Например, для функций а^х и log_ax a – это параметр.

4. Тригонометрические функции: y=sinx, y=cosx, y=tgx, y=ctgx. Аргументом является угол в радианах.

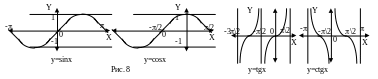
Функции y=sinx, y=cosx определены при всех значениях х, функция y=tgx определена на всей числовой оси, кроме точек: x=(2k+1)/2, (k=0, 1, 2,…), функция y=ctgx определена на всей числовой оси, кроме точек: x=k (k=0, 1, 2,…) (рис. 8)

5. Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx.

Эти функции являются обратными к тригонометрическим. Функция y=arcsinx определяется следующим образом: по заданному значению sinx=с, определяется у – угол в радианах, синус которого равен заданному значению с (задана хорда, найти длину дуги). Функция y=arccosx определяется так: по заданному значению cosx=с, определяется у – угол в радианах, косинус которого равен заданному значению с. Функция y=arctgx: задано значение tgx=с, у – величина угла, тангенс которого равен заданному значению с. Функция y=arcctgx: задано значение ctgx=с, у – величина угла, котангенс которого равен заданному значению с. Обратная функция определяется на интервале, на котором любое ее значение принимается только один раз. При определении функции, обратной к данной, значения функции и аргумента меняются ролями. Проще всего это понять, если задана таблица функции - по значению аргумента таблица позволяет определить значение функции. Эта же таблица может использоваться, как таблица обратной функции. Но тогда ею надо пользоваться по-другому. Среди значений функции надо отыскать значение, самое близкое к тому, которое задано, и в качестве ответа взять из таблицы аргумент, которому соответствует это значение функции. Например, при расчете угла наклона боковой грани египетской пирамиды , было получено, что tg=1,35. В Таблице значений тригонометрических функций Приложения находим, что такое значение тангенса соответствует углу, равному примерно 53,5.

Взаимно обратными являются и рассмотренные нами ранее функции:

показательная у=а^х и логарифмическая y=log_ax, степенная у=х^ и при разных значениях , например, у=х² и .

Функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (сложения, вычитания, умножения и деления) и операций подстановки ("взятие функции от функции"), называются элементарными функциями. Например, - элементарные функции.