Декартова система координат в трехмерном пространстве

Можно построить прямоугольную систему координат в пространстве. Прямоугольную систему координат в пространстве образуют три взаимно перпендикулярные оси X, Y и Z, проходящие через некоторую точку О. Точка О играет роль начала координат. На всех трех прямых должен быть определен масштаб.

Z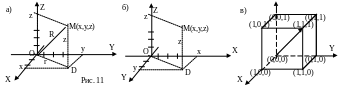

Ось X и ось Y, как и в случае прямоугольной системы координат на плоскости, называются осью абсцисс и осью ординат. Ось Z называется осью аппликат.

Положение любой точки М в пространстве задается тремя числами – координатами x, y и z. Они определяются следующим образом. Из точки М опустим перпендикуляры на ось Z и на плоскость XOY (точка D); из точки D опустим перпендикуляры на оси Х и Y. Длины отрезков, соединяющих точку О с основаниями 3-х перпендикуляров, и есть соответственно координаты x, y и z точки М (рис. 11а). Вообще говоря, можно применять как правую (рис. 11а), так и левую (рис. 11б) систему координат. Правая система координат соответствует правилу "правой руки" (большой палец вдоль оси Z, указательный – вдоль оси X, третий – вдоль оси Y), а левая система – правилу "левой руки". Обычно используется правая система (рис. 11а).

В черчении приняты некоторые стандарты изображения 3-х перпендикулярных друг другу прямых (под какими углами их рисовать). Для математических осей координат принято свободное изображение, как на рисунке 11а.

Расстояние R между двумя точками M₁(x₁,y₁,z₁) и M₂(x₂y₂,z₂) в 3-хмерной прямоугольной системе координат согласно теореме Пифагора равно:

, где

Например, геометрическое место точек, расстояние от которых до начала координат равно R (шар радиуса R): x²+y²+z²=R².

Пример

Найти длину диагонали единичного куба.

Решение:

Введем декартову систему координат, единица масштаба которой совпадает с величиной стороны куба. Вершины куба будут иметь координаты: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,1,0), (1,0,1), (1,1,1). Рассмотрим диагональ куба, начальной точкой которой является точка с координатами (0,0,0), а конечной точка (1,1,1). Длина всех диагоналей куба одинакова и равна длине этой диагонали, а ее длина равна: | |=

Векторы в трехмерном пространстве

В трехмерном пространстве вектор задается тремя координатами - = (x,y,z), где x, y, и z - величина проекции вектора на координатные оси.

Например, если начало вектора вектора = (1,1,1) поместить в начало координат, то его конец попадет в точку с координатами (1,1,1).

Пусть (x',y',z') связан с вектором (x,y,z) соотношением =k . Тогда: x'=kx, y'=ky, z'=kz.

Аналогично, пусть = (x₁,y₁,z₁), = (x₂,y₂,z₂), = (x₃,y₃,z₃) и . Тогда x₃=x₁+x_2, y₃=y₁+y₂ и z₃=z₁+z₂

Т.е. и в трехмерном пространстве при умножении вектора на число k его координаты умножаются на это число, а три координаты суммы векторов и равны сумме их соответствующих координат.

Сферические координаты

Сферические координаты в пространстве - это 3 координаты: r,  и . Первая координата r – расстояние от точки М до начала координат О,  и  - угловые координаты, хорошо знакомые всем из географии:  - долгота,  - угол, дополняющий широту  до 90, т.е. =90- (рис. 12а).

Значениям сферических координат в пределах 0r<, -<, 0 соответствуют все точки пространства.

Зависимость между сферическими координатами r, φ и  точки М и ее прямоугольными координатами x, y и z также выражается формулами, известными из тригонометрии:

x=rsincos, y=rsinsin, z=rcos - вычисление декартовых координат по сферическим,

- вычисление сферических координат по декартовым.

То есть, зная декартовы координаты точки, мы можем определить ее сферические координаты и наоборот. Зная ее сферические координаты, можно определить декартовы координаты.