Уравнение спирали Архимеда

Пусть по лучу, вращающемуся около полюса О с постоянной угловой скоростью , движется точка М с постоянной скоростью v. Тогда точка М опишет линию, которая называется спиралью Архимеда. Для того чтобы вывести уравнение этой линии, введем полярную систему координат, центр которой совпадает с точкой О, тогда расстояние от точки М до полюса О r=ОМ пропорционально углу  (рис 10а). Это означает, что уравнение спирали Архимеда можно записать в виде:

r=k.

В предыдущих главах мы строили опорные точки графика спирали Архимеда, руководствуясь именно этим свойством спирали – при изменении угла на величину nΔφ длину радиуса-вектора мы меняли на nΔr.

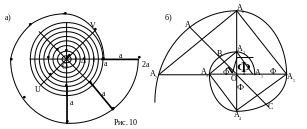
Из уравнения видно, что если =2 (точка М совершила полный оборот вокруг центра О), то r₁=k2, после второго оборота r₂=k4=2r₁, после третьего r₃=k6=3r₁ и т.д. Величина k2=а называется шагом спирали. Шаг спирали - это величина смещения вдоль луча, соответствующее повороту луча на 2.

Так как шаг спирали имеет ясный физический смысл, уравнение спирали Архимеда принято задавать в терминах именно шага спирали: . Коэффициент пропорциональности k и шаг спирали а связаны соотношением: и а=2k.

Уравнение логарифмической спирали

Опорные точки логарифмической спирали мы строили по следующему алгоритму – при повороте радиуса-вектора на угол Δφ его длину мы увеличивали в t раз, при повороте на 2Δφ в t² раз, при повороте на 3Δφ в t³ раз и т.д. Т.е. мы исходили из того, что логарифм длины радиуса-вектора является линейной функцией величины поворота φ. Такую зависимость описывает уравнение вида r=bq^ (logr=c+φlogq=c+kφ). Это и есть уравнение логарифмической спирали в полярных координатах. Оно демонстрирует, что какой бы первоначальный угол  мы ни взяли, в силу формулы q^+=q^q^ увеличению угла на значение  соответствует увеличение длины радиуса-вектора в q^ раз.

Математики обычно пишут уравнение r=bq^ в виде: r=be^k. Для того, чтобы представить уравнение r=bq^ в форме r=be^k, воспользуемся формулой определения логарифма: . Тем самым, и, следовательно: , где k=lnq. При приращении угла  на величину  длина радиуса-вектора увеличивается в t=q^=e^k раз, при увеличении на 2 в q^2=e^k2=t² раз и т.д. Логарифм длины радиуса-вектора с ростом угла поворота  растет линейно. Логарифмическая спираль пересекает все лучи, выходящие из точки О, под одним и тем же углом  (k=ctg). Из-за этого ее еще называют равноугольной спиралью (это ее свойство доказывается с помощью предельного перехода при n, где n - число частей, на которые делится окружность, из подобия всех треугольников, получающихся, если соединить отрезками соседние опорные точки; при таком переходе хорды стремятся к касательным). В качестве примера логарифмической спирали рассмотрим спираль раковины Nautilus (рис. 10б). Ее уравнение мы выведем, исходя из того условия, что при повороте на угол /2 длина радиуса-вектора увеличивается в раз (параметр а - это длина радиуса-вектора при =0, для простоты можем принять его равным 1). Легко видеть, что уравнение спирали можно написать в виде: . Из этого уравнения видно, что приращению угла на /4 соответствует увеличение длины радиуса-вектора в раз, а приращению угла на /8 соответствует увеличение длины радиуса-вектора в раз (чтобы вычислить эти значения, надо нажать на калькуляторе на кнопку 2 и 3 раза, соответственно). И для того, чтобы построить график спирали Nautilus по 16 опорным точкам, достаточно поделить окружность на 16 частей, вычислить с помощью калькулятора 16 членов геометрической прогрессии со знаменателем :

1, , ,  , , …,Ф² и последовательно отметить на 1-ом, 2-ом, 3-ьем и т.д. радиусах соответствующие длины. Из уравнения видно, что опорные точки А₁, А₂,…,А₇, по которым мы строили чертеж спирали, делят диаметры в золотой пропорции - А₃О:А₁О=А₄О:А₂О=…=Ф:1 и что это же верно и для всех вообще диаметров раковины Nautilus. Кроме того, виток спирали разбивает диаметр в золотой пропорции: А₅А₃:А₃А₁=(Ф²+Ф):(1+Ф)=Ф, аналогично А₆А₄:А₄А₂= (Ф²+Ф): (1+Ф)=Ф и из уравнения спирали следует, что для произвольного диаметра АС: АС:ВС=Ф

Вспомним сетку, построенную с помощью деления круга на 16 частей и окружностей, радиусы которых образуют геометрическую прогрессию с множителем q≈0,607. Такая сетка, как было показано, с неплохой точностью обеспечивает сохранение подобия. Так как радиусы окружностей - убывающие геометрические прогрессии, сетка задает опорные точки для дуг логарифмической спирали.